2024-2025学年山西省吕梁市兴县康宁中学数学九年级第一学期开学质量跟踪监视试题【含答案】

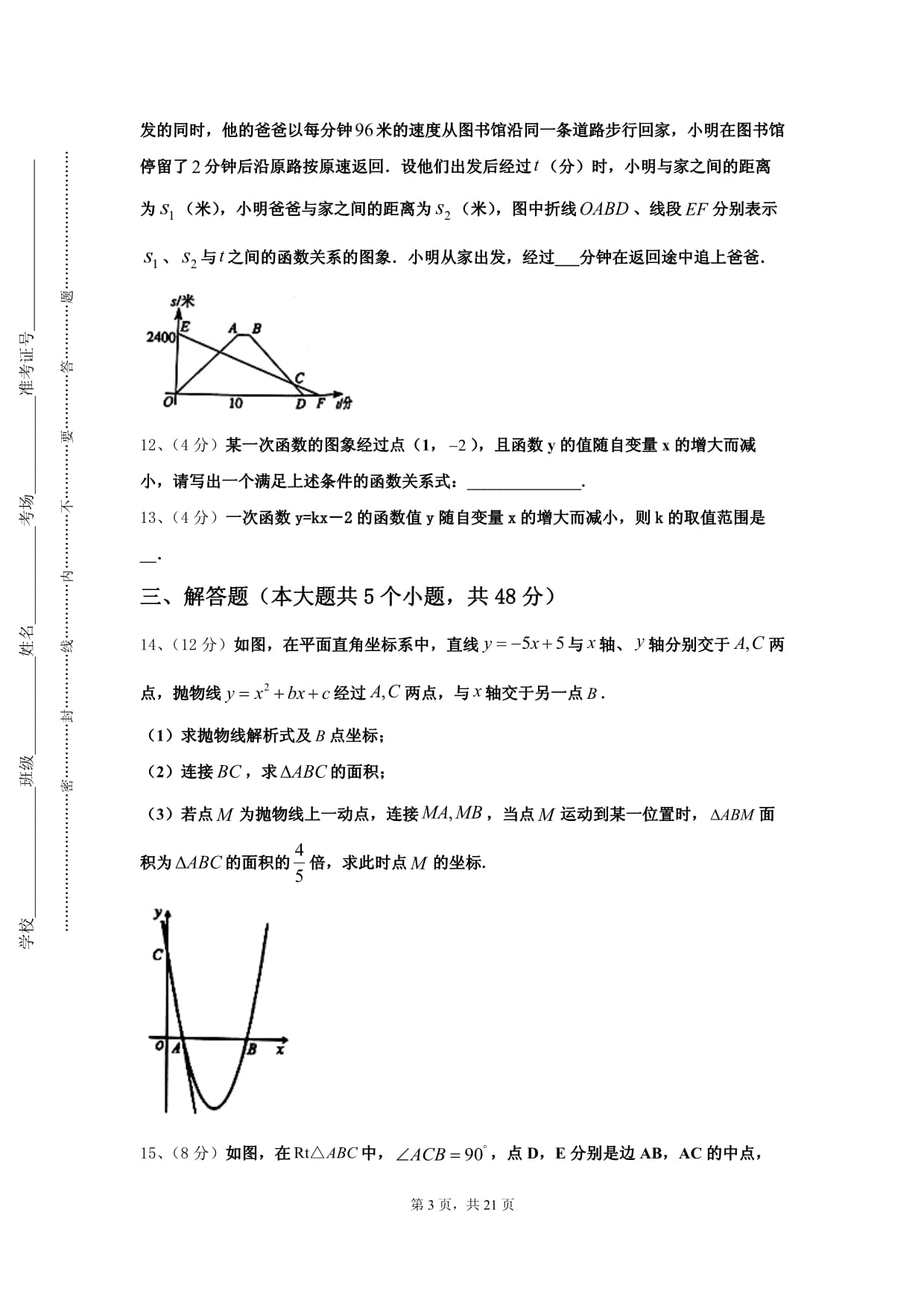
学校________________班级____________姓名____________考场____________准考证号学校________________班级____________姓名____________考场____________准考证号…………密…………封…………线…………内…………不…………要…………答…………题…………第1页，共5页2024-2025学年山西省吕梁市兴县康宁中学数学九年级第一学期开学质量跟踪监视试题题号一二三四五总分得分批阅人A卷（100分）一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）1、（4分）直角三角形两直角边长为5和12，则此直角三角形斜边上的中线的长是()A．5 B．6 C．6.5 D．132、（4分）如图，直线经过点A(a，)和点B(，0)，直线经过点A，则当时，x的取值范围是（）A．x>-1 B．x<-1 C．x>-2 D．x<-23、（4分）如图，在平行四边形ABCD中，，，AC，BD相交于点O，，交AD于点E，则的周长为A．20cm B．18cm C．16cm D．10cm4、（4分）如图，在中，点、分别是、的中点，平分，交于点，若，则的长是（）A． B． C． D．5、（4分）如图，点O（0，0），A（0，1）是正方形OAA1B的两个顶点，以OA1对角线为边作正方形OA1A2B1，再以正方形的对角线OA2作正方形OA1A2B1，…，依此规律，则点A2018的坐标是（）A．（﹣2018，0） B．（21009，0）C．（21008，﹣21008） D．（0，21009）6、（4分）如果直角三角形的边长为3，4，a，则a的值是()A．5 B．6 C． D．5或7、（4分）已知y-3与x成正比例,且x=2时,y=7,则y与x的函数关系式为(）A．y=2x+3 B．y=2x-3 C．y-3=2x+3 D．y=3x-38、（4分）要使二次根式x-3有意义，x的值可以是（）A．0 B．1 C．2 D．3二、填空题（本大题共5个小题，每小题4分，共20分）9、（4分）若一组数据的平均数为17，方差为2，则另一组数据的平均数和方差分别为（）A．17，2 B．18，2 C．17，3 D．18，310、（4分）已知等腰三角形有两条边分别是3和7，则这个三角形的周长是_______.11、（4分）小明租用共享单车从家出发，匀速骑行到相距米的图书馆还书．小明出发的同时，他的爸爸以每分钟米的速度从图书馆沿同一条道路步行回家，小明在图书馆停留了分钟后沿原路按原速返回．设他们出发后经过（分）时，小明与家之间的距离为（米），小明爸爸与家之间的距离为（米），图中折线、线段分别表示、与之间的函数关系的图象．小明从家出发，经过___分钟在返回途中追上爸爸．12、（4分）某一次函数的图象经过点（1，），且函数y的值随自变量x的增大而减小，请写出一个满足上述条件的函数关系式：______________.13、（4分）一次函数y=kx－2的函数值y随自变量x的增大而减小，则k的取值范围是__．三、解答题（本大题共5个小题，共48分）14、（12分）如图，在平面直角坐标系中，直线与轴、轴分别交于两点，抛物线经过两点，与轴交于另一点.（1）求抛物线解析式及点坐标；（2）连接，求的面积；（3）若点为抛物线上一动点，连接，当点运动到某一位置时，面积为的面积的倍，求此时点的坐标.15、（8分）如图，在中，，点D，E分别是边AB，AC的中点，连接DE，DC，过点A作交DE的延长线于点F，连接CF.（1）求证：；（2）求证，四边形BCFD是平行四边形；（3）若，，求四边形ADCF的面积.16、（8分）已知：如图，Rt△ABC中，∠ACB＝900，CD⊥AB，垂足为D，AF平分∠CAB，交CD于点E，交CB于点F.求证：CE＝CF．17、（10分）某工厂制作AB两种型号的环保包装盒．已知用3米同样的材料分别制成A型盒的个数比制成B型盒的个数少1个，且制作一个A型盒比制作一个B型盒要多用20%的材料．求制作每个A，B型盒各用多少材料？18、（10分）运城市某学校去年在某商场购买甲、乙两种不同足球，购买甲种足球共花费2000元，购买乙种足球共花费1400元，购买甲种足球数量是购买乙种足球数量的2倍.且购买一个乙种足球比购买一个甲种足球多花20元.（1）求购买一个甲种足球、一个乙种足球各需多少元；（2）今年为响应“足球进校园”的号召，这所学校决定再次购买甲、乙两种足球共50个.恰逢该商场对两种足球的售价进行调整，甲种足球售价比第一次购买时提高了，乙种足球售价比第一次购买时降低了.如果此次购买甲、乙两种足球的总费用不超过3000元，那么这所学校最多可购买多少个乙种足球？B卷（50分）一、填空题（本大题共5个小题，每小题4分，共20分）19、（4分）“等边对等角”的逆命题是．20、（4分）已知空气的密度是0.001239，用科学记数法表示为________21、（4分）已知5个数的平均数为，则这六个数的平均数为___22、（4分）如图，在四边形ABCD中，∠A+∠B=200°，作∠ADC、∠BCD的平分线交于点O1称为第1次操作，作∠O1DC、∠O1CD的平分线交于点O2称为第2次操作，作∠O2DC、∠O2CD的平分线交于点O3称为第3次操作，…，则第5次操作后∠CO5D的度数是_____．23、（4分）已知的对角线，相交于点，是等边三角形，且，则的长为__________．二、解答题（本大题共3个小题，共30分）24、（8分）如图，一次函数的图象与反比例函数的图象交于点和点．（1）求一次函数和反比例函数的解析式；（2）直接写出不等式的解集．25、（10分）实践活动小组要测量旗杆的高度,现有标杆、皮尺.小明同学站在旗杆一侧,通过观视和其他同学的测量,求出了旗杆的高度，请完成下列问题：(1)小明的站点，旗杆的接地点,标杆的接地点,三点应满足什么关系？(2)在测量过程中,如果标杆的位置确定,小明应该通过移动位置，直到小明的视点与点在同直一线上为止;(3)他们都测得了哪些数据就能计算出旗杆的高度?请你用小写字母表示这些数据(不允许测量多余的数据)；(4)请用(3)中的数据，直接表示出旗杆的高度.26、（12分）从甲地到乙地有两条公路，一条是全长600km的普通公路，另一条是全长480km的高速公路，某客车在高速公路上行驶的平均速度比在普通公路上快45km/h，由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半，求该客车由高速公路从甲地到乙地所需的时间．

参考答案与详细解析一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）1、C【解析】

根据勾股定理可求得直角三角形斜边的长,再根据直角三角形斜边上的中线等于斜边的一半即可求解【详解】∵直角三角形两直角边长为5和12∴斜边=13∴此直角三角形斜边上的中线的长=6.5故答案为:C此题考查直角三角形斜边上的中线和勾股定理，解题关键在于掌握直角三角形斜边上的中线等于斜边的一半2、A【解析】

先求出点A坐标，再结合图象观察出直线直线在直线下方的自变量x的取值范围即可.【详解】把A(a，-2)代入y2=2x，得-2=2a，解得：a=-1，所以点A(-1，-2)，观察图象可知当x>-1时，，故选A.本题考查了一次函数与一元一次不等式，观察函数图象，比较函数图象的高低(即比较函数值的大小)，确定对应的自变量的取值范围．注意数形结合思想的运用．3、A【解析】

根据平行四边形对角线互相平分可知点O是BD中点，继而可判断出EO是BD的中垂线，得出BE=ED，从而可得出△ABE的周长=AB+AD，即可得出答案．【详解】∵四边形ABCD是平行四边形，AC、BD交于点O，∴BO=DO，由∵EO⊥BD，∴EO是线段BD的中垂线，∴BE=ED，故可得△ABE的周长=AB+AD=20cm，故选A．本题考查了平行四边形的性质以及中垂线的判定及性质等，正确得出BE=ED是解题关键．4、B【解析】

先证明DE是中位线，由此得到DE∥AB，再根据角平分线的性质得到DF=BD，由此求出答案．【详解】∵点、分别是、的中点，∴DE是△ABC的中位线，BD=BC=3，∴DE∥AB，∴∠ABF=∠DFB,∵平分，∴∠ABF=∠CBF，∴∠DFB=∠CBF，∴BD=FD,∴DF=3，故选：B．此题考查三角形的中位线定理，等腰三角形的性质，角平分线的性质，熟记定理并运用解题是关键．5、B【解析】

根据正方形的性质找出点A1、A2、A3、A4、A5、A6、A7、A8、A9、A10、…的坐标，根据坐标的变化可找出变化规律“A8n+2（24n+1，0）（n为自然数）”，依此规律即可求出点A2018的坐标（根据点的排布找出第8n+2个点在x轴正半轴，利用排除法亦可确定答案）．【详解】解：∵A1（1，1），A2（2，0），A3（2，﹣2），A4（0，﹣4），A5（﹣4，﹣4），A6（﹣8，0），A7（﹣8，8），A8（0，16），A9（16，16），A10（32，0），…，∴A8n+2（24n+1，0）（n为自然数）．∵2018＝252×8+2，∴点A2018的坐标为（21009，0）．故选：B．本题考查了规律型：点的坐标，根据点的坐标的变化找出变化规律“A8n+2（24n+1，0）（n为自然数）”是解题的关键．6、D【解析】

分两种情况分析：a是斜边或直角边，根据勾股定理可得．【详解】解：当a是斜边时，a=；当a是直角边时，a=所以，a的值是5或故选：D．本题考核知识点：勾股定理，解题关键点：分两种情况分析．7、A【解析】

用待定系数法可求出函数关系式．【详解】y-1与x成正比例，即：y=kx+1，且当x=2时y=7，则得到：k=2，则y与x的函数关系式是：y=2x+1．故选：A．此题考查了待定系数法求一次函数解析式，利用正比例函数的特点以及已知条件求出k的值，写出解析式．8、D【解析】

根据二次根式有意义的条件可得x-3≥0，再解即可．【详解】由题意得：x−3⩾0，解得：x⩾3，故选：D.此题考查二次根式有意义的条件，解题关键在于掌握其定义.二、填空题（本大题共5个小题，每小题4分，共20分）9、B【解析】

根据平均数和方差的变化规律，即可得出答案．【详解】∵数据x1+1，x1+1，，xn+1的平均数为17，∴x1+1，x1+1，，xn+1的平均数为18，∵数据x1+1，x1+1，，xn+1的方差为1，∴数据x1+1，x1+1，，xn+1的方差不变，还是1；故选B．本题考查了方差与平均数，用到的知识点：如果一组数据x1，x1，，xn的平均数为，方差为S1，那么另一组数据ax1+b，ax1+b，，axn+b的平均数为a+b，方差为a1S1．10、17【解析】

根据等腰三角形的可得第三条边为3或7，再根据三角形的三边性质即可得出三边的长度，故可求出三角形的周长.【详解】依题意得第三条边为3或7，又3+3＜7，故第三条边不能为3，故三边长为3,7,7故周长为17.此题主要考查等腰三角形的性质，解题的关键是熟知三角形的构成条件.11、1.【解析】

用路程除以时间就是小亮骑自行车的速度；设小亮从家出发，经过x分钟，在返回途中追上爸爸，再由题意得出等量关系除了小亮在图书馆停留2分钟，即x-2分钟所走的路程减去小亮从家到图书馆相距的2400米，就是小亮在返回途中追上爸爸时，爸爸所走的路程，列出方程即可解答出来【详解】解：小亮骑自行车的速度是2400÷10=240m/min；

先设小亮从家出发，经过x分钟，在返回途中追上爸爸，由题意可得：

（x-2）×240-2400=96x

240x-240×2-2400=96x

144x=2880

x=1．

答：小亮从家出发，经过1分钟，在返回途中追上爸爸．此题考查一次函数的实际运用，根据图象，找出题目蕴含的数量关系，根据速度、时间、路程之间关系解决问题．12、y=-x-1(答案不唯一)．【解析】

根据y随着x的增大而减小推断出k＜1的关系，再利用过点（1，-2）来确定函数的解析式．【详解】解：设一次函数解析式为y=kx+b,∵一次函数y随着x的增大而减小，

∴k＜1．

又∵直线过点（1，-2），

∴解析式可以为：y=-x-1等．

故答案为：y=-x-1(答案不唯一)．此题主要考查了一次函数的性质，得出k的符号进而求出是解题关键．本题是开放题，答案不唯一。13、k＜1【解析】

根据一次函数图象的增减性来确定k的符号即可.【详解】解：∵一次函数y=kx-2的函数值y随自变量x的增大而减小，∴k＜1，故答案为k＜1．本题考查了一次函数图象与系数的关系．在直线y=kx+b（k≠1）中，当k＞1时，y随x的增大而增大；当k＜1时，y随x的增大而减小．三、解答题（本大题共5个小题，共48分）14、（1），；（2）；（3）点的坐标为，，，见解析.【解析】

（1）利用两点是一次函数上的点求出两点，再代入二次函数求解即可.（2）根据，求出，求出△ABC.（3）根据面积为的面积的倍，求出，得出求出此时M的坐标即可.【详解】（1）解：∵直线∴令，则，解得∴令，则，∴将点，代入中得，，解得∴抛物线的解析式为：；令，则，解得∴.（2）解：∵，∴∴（3）∵面积为的面积的倍，∴∵AB=4,∴，∵∴抛物线的顶点坐标为符合条件，当时，，解的，x1=，x2=，∴点的坐标为（3，-4），，.本题考查的是二次函数，熟练掌握二次函数是解题的关键.15、（1），见解析；（2）四边形BCFD是平行四边形，见解析；（3）.【解析】

（1）欲证明DE=EF，只要证明△AEF≌△CED即可；

（2）只要证明BC=DF，BC∥DF即可；

（3）只要证明AC⊥DF，求出DF、AC即可；【详解】（1）证明：∵，∴，∵，，∴，∴．（2）∵，，∴，，∵，∴，∴四边形BCFD是平行四边形．（3）在中，，，∴，，，∴，∵DE∥BC，∴，∴，∴.本题考查平行四边形的判定和性质、三角形的中位线定理．解直角三角形等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．16、见解析.【解析】

根据三角形的内角和定理得出∠CAF+∠CFA=90°，∠FAD+∠AED=90°，根据角平分线和对顶角相等得出∠CEF=∠CFE，根据等腰三角形的判定推出即可。【详解】证明：∵∠ACB=90°，CD⊥AB，

∴∠CDA=90°，

∴∠CAF+∠CFA=90°，∠FAD+∠AED=90°，

∵AF平分∠CAB，

∴∠CAF=∠FAD，

∴∠CFA=∠AED=∠CEF，即∠CEF=∠CFE

∴CE=CF．本题考查了直角三角形性质，等腰三角形的性质和判定，三角形的内角和定理，关键是推出∠CEF=∠CFE．17、制作每个A型盒用0.1米材料，制作每个B型盒用0.5米材料．【解析】

设制作每个B型盒用x米材料，则制作每个A型盒用（1+20%）x米材料，根据数量＝材料总数÷每个环保包装盒所需材料结合用3米同样的材料分别制成A型盒的个数比制成B型盒的个数少1个，即可得出关于x的分式方程，解方程并经检验后即可得出结论．【详解】设制作每个B型盒用x米材料，则制作每个A型盒用（1+20%）x米材料，依题意得：﹣＝1，解得：x＝0.5，经检验，x＝0.5是所列分式方程的解，且符合题意，∴（1+20%）x＝0.1．答：制作每个A型盒用0.1米材料，制作每个B型盒用0.5米材料．本题考查分式方程的应用，正确得出题中等量关系是解题关键．18、（1）购买一个甲种足球需50元，购买一个乙种足球需70元；（2）最多可购买31个乙种足球.【解析】

（1）设购买一个甲种足球需x元，根据：购买足球数＝总费用÷单价，购买甲种足球的数量＝2×购买乙种足球数量，列出方程求解即可；（2）设这所学校再次购买y个乙种足球，根据：购买甲足球费用＋购买乙足球费用≤3000，列出不等式，求解得结论．【详解】（1）解：设购买一个甲种足球需元，则购买一个乙种足球需元，由题意得：，解得：经检验，是原方程的解，答：购买一个甲种足球需50元，购买一个乙种足球需70元.（2）设这所学校再次购买个乙种足球，则购买个甲种足球，由题意得：解得：，答：最多可购买31个乙种足球.本题解题关键：在于弄清已知数与所求量的数量关系，建立联系，特别注意的是分式方程在应用题里面也需要检验.一、填空题（本大题共5个小题，每小题4分，共20分）19、等角对等边【解析】试题分析：交换命题的题设和结论即可得到该命题的逆命题；解：“等边对等角”的逆命题是等角对等边；故答案为等角对等边．【点评】本题考查了命题与定理的知识，解题的关键是分清原命题的题设和结论．20、1.239×10-3.【解析】

绝对值小于1的数也可以利用科学记数法表示，一般形式为a×10-n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．【详解】0.001239=1.239×10-3故答案为：1.239×10-3.本题考查了科学记数法的表示，熟练掌握n的值是解题的关键.21、【解析】

根据前5个数的平均数为m，可得这5个数的总和，加上第6个数0，利用平均数的计算公式计算可得答案.【详解】解：∵∴∴∴这六个数的平均数此题主要考查了算术平均数的含义和求法，要熟练掌握，解答此题的关键是判断出：.22、175°【解析】如图所示，∵∠ADC、∠BCD的平分线交于点O1，∴∠O1DC+∠O1CD=（∠ADC+∠DCB），∵∠O1DC、∠O1CD的平分线交于点O2，∴∠O2DC+∠O2CD=（∠O1DC+∠O1CD）=（∠ADC+∠DCB），同理可得，∠O3DC+∠O3CD=（∠O2DC+∠O2CD）=（∠ADC+∠DCB），由此可得，∠O5DC+∠O5CD=（∠O4DC+∠O4CD）=（∠ADC+∠DCB），∴△CO5D中，∠CO5D=180°﹣（∠O5DC+∠O5CD）=180°﹣（∠ADC+∠DCB），又∵四边形ABCD中，∠DAB+∠ABC=200°，∴∠ADC+∠DCB=160°，∴∠CO5D=180°﹣×160°=180°﹣5°=175°，故答案为175°．23、．【解析】

根据等边三角形的性质得出AD=OA=OD，利用平行四边形的性质和矩形的判定解答即可．【详解】解：∵△AOD是等边三角形，

∴AD=OA=OD=4，

∵四边形ABCD是平行四边形，

∴OA=AC，OD=BD，

∴AC=BD=8，

∴四边形ABCD是矩形，

在Rt△ABD中，，

故答案为：．此题考查平行四边形的性质，关键是根据平行四边形的性质解答即可．二、解答题（本大题共3个小题，共30分）24、（1），；（2）或．【解析】

（1）将点A的坐标代入反比例函数的解析式可求得m的值，从而得到反比例函数的解析式，然后将点B的坐标代入可求得n的值，接下来，利用待定系数法求得直线AB的解析式即可；

（2）不等式的解集为直线y=kx+b位于反比