零阶保持器离散系统的数学描述z变换差分方程脉冲传课件

总结与复习自动控制原理2总结与复习自动控制原理21第六章频率响应综合法系统综合：根据系统已知部分的特性，确定校正方式和校正装置，使系统的整体特性符合要求。

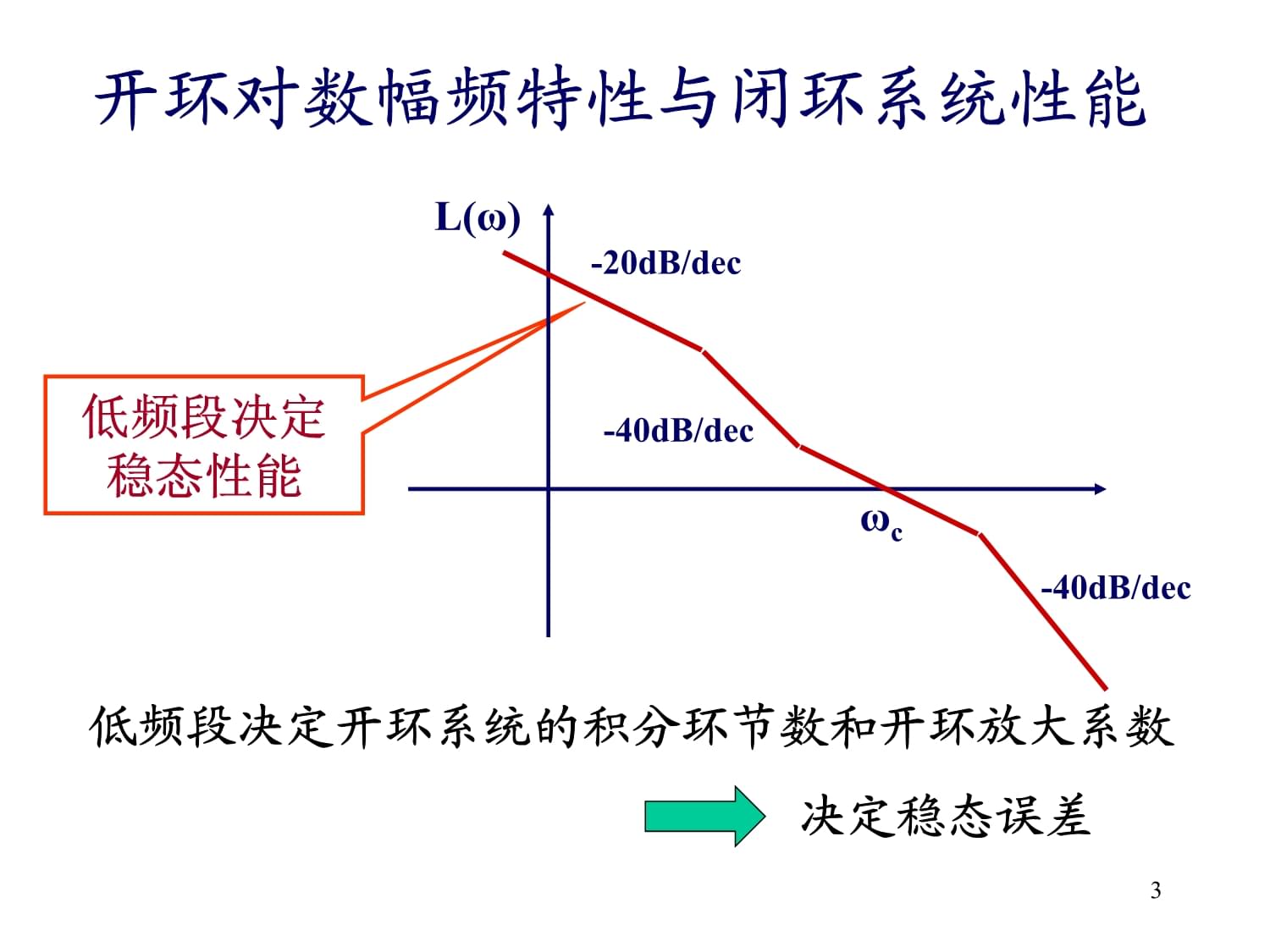
综合的核心是设计校正装置。校正方式：串联（重点）、反馈、前馈、复合。频域综合：设计校正装置，使开环频率特性曲线（主要是幅频特性的Bode图）满足要求。第六章频率响应综合法系统综合：综合的核心是设计校正装置。2低频段决定稳态性能L(ω)-40dB/dec-40dB/decωc-20dB/dec开环对数幅频特性与闭环系统性能低频段决定开环系统的积分环节数和开环放大系数决定稳态误差低频段决定稳态性能L(ω)-40dB/dec-40dB/de3中频段决定暂态性能：保证稳定裕量和恰当的截止频率L(ω)-40dB/dec-40dB/dec-20dB/decω2ω3ωc-20dB/dech中频宽稳定裕量↑平稳性↑；截止频率（幅穿频率）↑快速性↑，但抗高频干扰能力↓最小相位系统较理想的中频段中频段决定暂态性能：保证稳定裕量和恰当的截止频率L(ω)-44高频段决定系统抑制高频噪声的能力高频段高频段衰减越快，抗高频噪声能力越强；但会使稳定裕量和截止频率减小，平稳性和快速性下降。L(ω)-40dB/dec-40dB/dec-20dB/decω2ω3ωch-20dB/dec高频段决定系统抑制高频噪声的能力高频段高频段衰减越快，抗高频5串联校正的两种常用思路根据性能要求确定希望的开环频率特性的Bode图，再由Bode图求开环传递函数，最后得到校正装置的传递函数。限定校正装置为简单结构，通过改变其参数来获得尽可能好的开环频率特性。思路2的常用校正方式：超前校正，迟后校正，迟后超前校正串联校正的两种常用思路根据性能要求确定希望的开环频率特性的B6超前校正：-R(s)Y(s)E(s)迟后校正：迟后超前校正：超前校正：-R(s)Y(s)E(s)迟后校正：迟后超前校正：700°超前校正作用：利用相角超前特性增大相角裕量，利用正斜率幅频特性增大截止频率，从而改善暂态性能。两种校正思路：按相角裕量，或按提升幅值以增大ωc00°超前校正作用：利用相角超前特性增大相角裕量，利用正斜率8校正思路1：0°校正思路1：0°9校正思路2：0°校正思路2：0°100°-90°0迟后校正作用：利用幅值衰减特性，使截止频率下降，从而增大稳定裕量，改善响应的平稳性，但快速性降低。0°-90°0迟后校正作用：利用幅值衰减特性，使截止频率下降11迟后校正的计算校正前迟后校正的计算校正前1200°-90°90°-20dB/dec20dB/dec迟后超前校正作用：利用超前校正增大γ，利用迟后校正的幅值衰减特性使ωc满足要求。00°-90°90°-20dB/dec20dB/dec迟后超13迟后超前校正的设计思路ωL(ω)-20dB/dec-40-60校正前超前校正-20超前校正后-20-40-60ba迟后校正迟后超前校正的设计思路ωL(ω)-20dB/dec-40-614计算步骤计算步骤15零阶保持器离散系统的数学描述z变换差分方程脉冲传课件16状态空间方法（现代控制理论）数学模型——一阶微分方程组分析——时域核心内容——状态变量的可控、可观性设计——状态反馈、极点配置、最优控制状态信息的获取——状态观测器（涉及第二、三、七、八章）状态空间方法（现代控制理论）数学模型——一阶微分方程组（涉17线性系统状态空间表达式的一般形式A、B、C、D为常数阵定常系统A、B、C、D含时变参数时变系统系统u(t)y(t)线性系统状态空间表达式的一般形式A、B、C、D为常数阵18同一系统的状态空间表达式不唯一设系统的两种状态空间表达式分别为系统u(t)y(t)和则状态变量之间存在线性变换关系线性变换的作用：将模型转化为简单表达形式，如对角规范形、约当标准形、可控或可观规范形等若线性变换为非奇异的（P-1存在），则有同一系统的状态空间表达式不唯一设系统的两种状态空间表达式分别19非奇异线性变换的性质（1）线性变换不改变系统的特征值（2）线性变换不改变系统的传递函数（3）线性变换不改变系统的可控、可观性非奇异线性变换的性质（1）线性变换不改变系统的特征值（2）线20两类模型的相互转化由微分方程或传递函数转化为状态空间模型

（不唯一，有多种方法，重点是直接分解法）系统u(t)y(t)G(s)U(s)Y(s)A,B,C,D由状态空间模型转化为传递函数（阵）

（唯一。注意：限于定常系统）两类模型的相互转化由微分方程或传递函数转化为状态空间模型

（21状态空间描述下的运动分析齐次状态方程的解：状态转移矩阵的性质？状态空间描述下的运动分析齐次状态方程的解：状态转移矩阵的性质22非齐次状态方程的解：主要是利用状态转移矩阵求解状态方程非齐次状态方程的解：主要是利用状态转移矩阵求解状态方程23状态转移矩阵的计算：①拉氏变换法②对角标准形法设矩阵A的特征值相异，对角变换为状态转移矩阵的计算：①拉氏变换法②对角标准形法设矩阵A24状态可控性线性定常系统完全可控的充要条件为Qc：可控性判别阵说明：状态可控性线性定常系统完全可控的充要条件为Qc：可控性判别25状态可观测性线性定常系统完全可观测的充要条件为说明：状态可观测性线性定常系统完全可观测的充要条件为说明：26状态空间综合法1.状态反馈加入状态反馈后的系统结构图K-B∫CA状态空间综合法1.状态反馈加入状态反馈后的系统结构图K-B27零阶保持器离散系统的数学描述z变换差分方程脉冲传课件282.状态反馈与闭环极点配置极点配置条件：全部闭环极点的充要条件为：状态完全可控通过状态反馈对于可任意配置2.状态反馈与闭环极点配置极点配置条件：全部闭环极点的充要29全维状态观测器B∫CAB∫A－HCH状态观测器A－HC的特征值为状态观测器的极点全维状态观测器B∫CAB∫A－HCH状态观测器A－HC的特30状态观测器的极点配置状态观测器的闭环极点可任意配置的充要条件为

系统状态完全可观测状态观测器的极点配置状态观测器的闭环极点可任意配置的充要条件31基于状态观测器的状态反馈系统B∫CAB∫A－HCH观测器K-基于状态观测器的状态反馈系统B∫CAB∫A－HCH观测器K-32极点配置的分离性原理状态观测器、状态反馈两部分的极点可以分别独立地进行配置。为使观测器的状态估计值较快地→实际状态，一般取观测器极点的负实部为状态反馈系统极点负实部的2～3倍。注：分离性原理基于精确模型极点配置的分离性原理状态观测器、状态反馈两部分的极点可以分别33闭环传递函数的不变性但闭环传递函数等同于直接状态反馈的情况，即注：闭环传递函数不变只意味着在初始状态为零、没有扰动、且模型准确时，无论是否有观测器，系统的输入输出特性不变；但其他情况下，有无观测器的系统性能是不一样的，且通常都是直接状态反馈系统的性能更好。闭环传递函数的不变性但闭环传递函数等同于直接状态反馈的情况，34第九章离散控制系统信号的采样与保持

采样过程与采样定理，零阶保持器离散系统的数学描述

z变换，差分方程，脉冲传递函数（开环、闭环）离散系统的z域分析法

稳定性，极点分布与暂态性能，稳态误差第九章离散控制系统信号的采样与保持

采样过程与采样35采样信号可看作是经载波信号调制后的结果：一、采样过程t0f(t)t0t0f*(t)1T2T2TT采样器信号的采样与保持采样信号可看作是经载波信号调制后的结果36采样信号的拉氏变换理想单位脉冲序列采样信号为二、采样信号的数学表达式采样信号的拉氏变换理想单位脉冲序列采样信号为二、采样信号的数37采样周期的选取：信号变化越快，采样周期应越小。三、香农（Shannon）采样定理则经采样得到的离散信号可以无失真地恢复为原连续信号的条件是0采样周期的选取：信号变化越快，采样周期应越小。三、香农（Sh38零阶

保持器t0T2T3T4Tt0T2T3T4T四、零阶保持器零阶保持器的传递函数：零阶

保持器t0T2T3T4Tt0T2T3T4T四、零阶保持39Z变换与Z反变换Z变换的常用求法：级数求和法（直接根据定义）部分分式法（对拉氏变换进行分解）Ｚ变换的基本性质：线性定理，延迟定理，超前定理，终值定理，初值定理，位移定理，Z域微分定理等Z反变换：长除法，部分分式法（通常分解F(z)/z）Z变换与Z反变换Z变换的常用求法：级数求和法（直接根据定义）40脉冲传递函数u(t)TG

(s)u*(t)Ty*(t)y(t)U(z)G

(z)Y(z)脉冲传递函数u(t)TG(s)u*(t)Ty*(t)y(t41开环脉冲传递函数

（注意有无采样开关隔开）u(t)TG1(s)u*(t)Tv*(t)G2(s)Ty*(t)u(t)TG1(s)u*(t)G2(s)Ty*(t)开环脉冲传递函数

（注意有无采样开关隔开）u(t)TG1(s42有零阶保持器的开环脉冲传递函数u(t)TGh(s)u*(t)G0(s)Ty*(t)零阶保持器有零阶保持器的开环脉冲传递函数u(t)TGh(s)u*(t)43闭环脉冲传递函数TG(s)H(s)－闭环脉冲传递函数TG(s)H(s)－44D*(s)TG(s)TH(s)－D*(s)TG(s)TH(s)－45脉冲传递函数与差分方程U(z)G

(z)Y(z)利用超前定理利用延迟定理脉冲传递函数与差分方程U(z)G(z)Y(z)利用超前定理46离散系统的稳定性R(z)Y(z)Z平面ImRe01-1稳定条件（开、闭环）：即系统的极点全部位于Z平面的单位圆内。低阶系统可直接求系统的极点，高阶系统则可利用双线性变换（不止一种形式）在W平面应用劳斯判据。离散系统的稳定性R(z)Y(z)Z平面ImRe01-1稳定47离散系统极点分布与暂态性能0jZ平面的极点1R(z)Y(z)0j期望的极点分布区域1期望区域离散系统极点分布与暂态性能0jZ平面的极点1R(z)Y(z)48离散系统的稳态误差D(z)G(z)-跟踪稳态误差为零的条件为闭环系统稳定开环传函Gk(z)包含与参考输入R(z)相同的不稳定极点

（内模原理）可用终值定理求离散系统的稳态误差D(z)G(z)-跟踪稳态误差为零49求稳态误差的分式分解法可用于任意输入，但主要用于正弦类输入D(z)G(z)-E2(z)的极点只有三种情况：①单位圆外（发散），②单位圆上的1（恒值或发散），③单位圆上1以外的位置（等幅振荡或发散，分解法主要用于这种情况）。求稳态误差的分式分解法可用于任意输入，但主要用于正弦类输入D50第十章非线性控制系统非线性系统的特点典型非线性特性及其特征（死区、饱和、间隙、继电特性）二阶线性系统的相轨迹（与极点的关系）相轨迹的绘制（解析法，等倾线法）由相轨迹图求时间及时间响应（积分法，增量法）非线性控制系统的相平面分析第十章非线性控制系统非线性系统的特点