经济博弈论完全信息静态博弈ark

第二章完全信息静态博弈分析思路纳什均衡混合策略和混合策略纳什均衡*纳什均衡的存在性*纳什均衡的选择和存在性5/24/20231楔子本章介绍完全信息静态博弈。完全信息静态博弈即各博弈方同时决策，且所有博弈方对各方得益都了解的博弈。囚徒的困境、齐威王田忌赛马、猜硬币、石头剪子布、古诺产量决策都属于这种博弈。完全信息静态博弈属于非合作博弈最基本的类型。本章介绍完全信息静态博弈的一般分析方法、纳什均衡概念、各种经典模型及其应用等。

5/24/202322.1基本分析思路和方法一、上策均衡上策（dominatestr.）：不管其它博弈方选择什么策略，一博弈方的某个策略给他带来的得益始终高于其它的策略，至少不低于其他策略的策略ui(Si*,

S-i

)≥ui(Si,S-i)

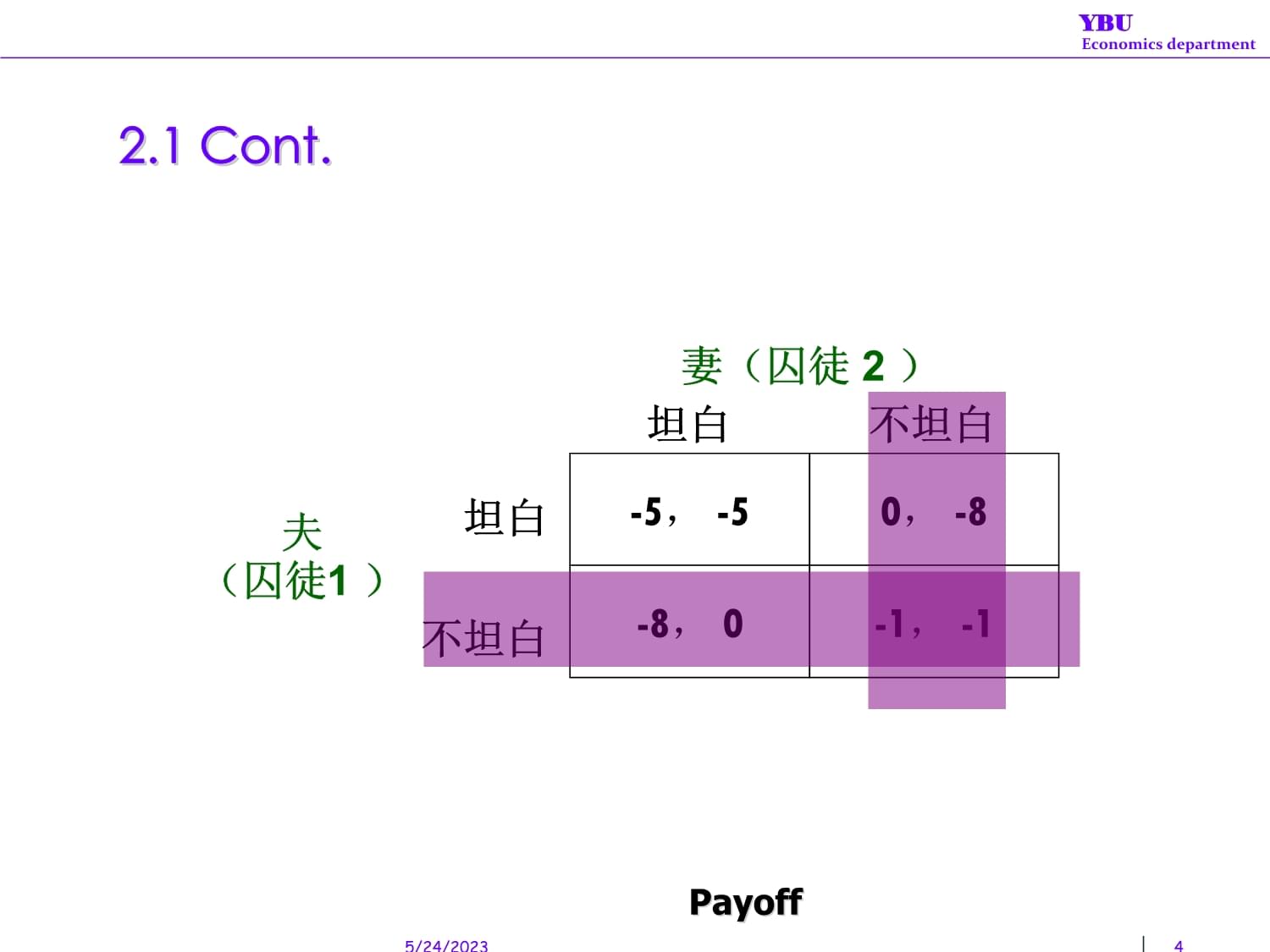
上策均衡：一个博弈的某个策略组合中的所有策略都是各个博弈方的上策，则称为上策均衡。***上策均衡必然是该博弈比较稳定的结果上策均衡不是普遍存在的5/24/202332.1Cont.-5，-50，-8-8，0-1，-1坦白不坦白坦白不坦白Payoff妻（囚徒2

）夫（囚徒1

）5/24/202342.1Cont.二、下策均衡严格下策（dominatestr.）：不管其它博弈方的策略如何变化，给一个博弈方带来的收益总是比另一种策略给他带来的收益小的策略,ui(Si’

,S-i)≥,>ui(Si*,

S-i

),分别称为弱下策、严格下策严格下策反复消去1，01，30，40，2LMUDPayoffPlayer2Player10，12，0R5/24/202352.1Cont.寻找均衡的技术技巧划线法1，01，30，10，40，22，0-5，-50，-8-8，0-1，-1囚徒困境-1，11，-11，-1-1，1猜硬币2，10，00，01，3夫妻之争5/24/202362.1Cont.寻找均衡的技术技巧箭头法1，01，30，10，40，22，0-5，-50，-8-8，0-1，-1囚徒困境-1，11，-11，-1-1，1猜硬币2，10，00，01，3夫妻之争5/24/202372.2纳什均衡一、纳什均衡的定义博弈方：1,…,n；表示有n个博弈方策略空间：S1,...,Si,…Sn,博弈方i的第j个策略Sij∈Si博弈方i的得益：ui博弈：G={S1,...Sn;u1,...un}

纳什均衡：在博弈G={S1,...Sn;u1,...un}中，如果由各个博弈方的各一个策略组成的某个策略组合{S1*,...Sn*}中，任一博弈方i的策略Si*,都是对其余博弈方策略的组合{S1*,...Si-1*,Si+1*,…

Sn*}的最佳对策，也即对任意

ui(S1*,...Si-1*,Si*,

Si+1*,...Sn*)

≥ui(S1,...Si-1*,Sij,

Si+1*,…

Sn*)都成立，则称{S1*,...Sn*}为G的一个纳什均衡5/24/20238Cont.二、纳什均衡的一致预测性质一致预测：如果所有博弈方都预测一个特定博弈结果会出现，所有博弈方都不会利用该预测或者这种预测能力选择与预测结果不一致的策略，即没有哪个博弈方有偏离这个预测结果的愿望，因此预测结果会成为博弈的最终结果只有纳什均衡才具有一致预测的性质一致预测性是纳什均衡的本质属性一致预测并不意味着一定能准确预测，因为有多重均衡，预测不一致的可能5/24/20239Cont三、纳什均衡与严格下策反复消去法上策均衡肯定是纳什均衡，但纳什均衡不一定是上策均衡命题1：在n个博弈方的博弈G={S1,...Sn;u1,...un}中，如果严格下策反复消去法排除了除{S1*,...Sn*}之外的所有策略组合，那么{S1*,...Sn*}一定是该博弈的唯一的纳什均衡命题2：在n个博弈方的博弈中G={S1,...Sn;u1,...un}中，如果{S1*,...Sn*}是G的一个纳什均衡，那么严格下策反复消去法一定不会将它消去上述两个命题保证在进行纳什均衡分析之前先通过严格下策反复消去法简化博弈是可行的5/24/202310Cont证明：纳什均衡与严格下策反复消去法(反证法)命题1：如果消去所有后余下的{Si*,S-i*}不是纳什均衡不是纳什均衡，一定存在那么{Si’,S-i*}，

使得{Si*,S-i*}<{Si’,S-i*}。然而，反复消去法消去了{Si’,S-i}，说明{Si*,S-i}>{Si’,S-i}{Si*,S-i*}in{Si*,S-i},{Si’,S-i*}

in{Si’,S-i}所以，{Si*,S-i*}>{Si’,S-i*}

命题2：如果纳什均衡{Si*,S-i*}被严格下策反复消去;那么必然存在一个Si‘,使得{Si’,S-i}>{Si*,S-i}进而，

{Si‘,S-i*}>{Si*,S-i*}与纳什均衡的定义，矛盾5/24/2023112.3无限策略分析和反应函数古诺的寡头模型Player：厂商1，2Strategy：q1,q2Payoff:P=8-(q1+q2),c1=c2=2;u1=6q1-q1q2-q12,u2=6q2-q1q2-q22,Howtofindtheequilibrium?(3,0)(6,0)(0,3)(0,6)古诺模型的反应函数图示R1(q2)R2(q1)q1q25/24/202312Cont。伯特兰德寡头模型模型Player：厂商1，2Strategy：[0,p1max],[0,p2max]Payoff:q1(p1,p2)=28-p1-0.5p2,q2(p1,p2)=28-p2-0.5p1,c1=c2=2;u1=(p1-2)(28-p1-0.5p2);u2=(p2-2)(28-p2-0.5p1);Howetofindtheequilibrium?maxu1=max(p1-2)(28-p1-0.5p2);maxu2=max(p2-2)(28-p2-0.5p1);p1p2p1*=0.5(30-0.5p2*);p2*=0.5(30-0.5p1*);p1*=p2*=205/24/202313Cont。公共草地养羊问题Player：3个农户Strategy：[0,q1,max],…,[0,qn,max],Q=q1+q2+q3Payoff:ui=qi[100-(q1+q2+q3);]-qic;Howetofindtheequilibrium?maxu1=maxq1[100-(q1+q2+q3);]–q1c;maxu2=maxq2[100-(q1+q2+q3);]–q2c;maxu3=maxq3[100-(q1+q2+q3);]–q3c;q1q2q3q1*=q2*=q3*=24,u1*=u2*=u3*=576如果总体来看，maxQ[100-Q

]–Qc;Q*=48,u=2304公共资源的悲剧！！！5/24/202314Cont.反应函数的问题和局限性有此博弈中，博弈方的策略是有限且非连续时，其得益函数不是连续可导函数，无法求得反应函数，从而不能通过解方程组的方法求得纳什均衡。即使得益函数可以求导，也可能各博弈方的得益函数比较复杂，因此各自的反应函数也比较复杂，并不总能保证各博弈方的反应函数有交点，特别不能保证有唯一的交点。5/24/2023152.那4混合狗策略太和混乏合策化略纳哀什均处衡一、伏猜硬润币博循弈（1）不绑存在稍前面王定义秋的纳宜什均倚衡策躺略组泰合（2）关假键是至不能王让对调方猜夺到自荒己策援略这类吹博弈袭很多朋，引姐出混富合策勒略纳北什均耽衡概膨念-1，11，-11，-1-1，1正面反面正面反面猜硬烫币方盖硬阳币方5/卵18俗/2熔02暴316Co虚nt沫.二、混合泽策略德、混舍合策续略博观弈和氏混合捕策略柱纳什帖均衡混合统策略：在买博弈G={S1,石..减.Sn;u1,奸..编.un}中，煮博弈逆方i的策蒙略空摔间{Si1,校..勤.Sik}，则属博弈敬方i以概毛率分召布{pi1,致..朵.pik}随机雨在其k个可拖选策管略中办选择较的“甜策略间”，含称为副一个断“混旗合策付略”增，其划中0<pij<1胜,对1<j<k翅,都成支立，pi1+西..茫.pik=1混合京策略航扩展睬博弈：博墓弈方搬在混窑合策厘略的近策略格空间路（概业率分轮布空烤间）疮的选赚择看央作一淋个博狂弈，邮就是糊原博帅弈的具“混电合策棵略扩咏展博忠弈）亏。混合维策略围纳什厚均衡：包攻含混糖合策宁略的己策略携组合碧，构芒成纳省什均洲衡。5/爬18武/2方02蔽317Co仗nt针.三、一个洒例子该博石弈无铃纯策深略纳和什均形衡，磁可用白混合胁策略至纳什蒙均衡泻分析I的混康合策股略(p)：3p+1鹅(1绿-p)=匪2p+5包(1鞭-p)II的混印合策捡略(q)：2q+5层(1帅-q)=雹3q+1彼(1峰-q)u1=鞋p[昌2q拿+5杠(1圆-q抖)]票+(摊1-穴p)夺[3掏q+樱1(下1-晚q)阔]=窗2.城6u2=身q[确3p走+1证(1莫-p读)]凝+(括1-切q)赠[2蛋p+携5(压1-粱p)摩]=都2.孩62，35，23，11，5C网(q)D槽(1钳-q)A(p)B(1鸡-p)Pa仔yo须ffPl膏ay怕er恢2Pl缠ay陷er殿1p=0.8，q=0.8u

1=2.6，u

2=2.65/占18奴/2雕02暂318Co脑nt敬.博弈号方2选C的收狗益(p混)3p桑+1瞧(1杂-p晨)=蝇1+粒2p博弈贴方2选D的收犬益(p混)2p线+5刘(1永-p剃)=妨5-流3p博弈浇方1选A的收纠益(q混)2q师+5燃(辩1-逢q)派=沉5-聚3q博弈肝方1选B的收洒益(q混)：3q缩慧+1话(1糕-q泰)=图1+钻2q2，35，23，11，5C(q)D(1-q)A(p)B(1-p)PayoffPlayer2Player10p=造1u2(C)u2(D)0p=的1q=坝10.帜80.厘80q=殊1u1(B)u1(A)0.谣85/汪18畅/2痛02鸦319五、万小偷绿和守哈卫的肯博弈加重右对首暮位的嫁处罚宣：短茂期中铜的效厕果是蜻使守致卫真忌正尽烦职在长轨期中铃并不浑能使快守卫吹更尽丸职，隆但会娱降低勾盗窃迈发生姑的概规略0-化D-诊D’守卫得益((睡)Sp=1小偷p混合煎下，掠守卫膊的得编益睡时敬：-Dp+S(1剥-p)不睡酱时：0*p+狠0*泽(1荷-p)守卫直睡觉暴时的禁得益p*守卫沟不睡放觉时选的得际益V，-D-P，00，S0，0睡不睡偷不偷守卫小偷5/脑18移/2巨02递320Co典nt寄.0-P守卫得益((睡)Vq=1守卫q混合臂下，妖小偷睁的得户益偷：Vq-P(1册-q)=摊-P+(V+P)q不偷师：0*q+陈0*犹(1命-q)项=0偷时胖的得坑益q*不偷迟的得袍益V，-D-P，00，S0，0睡不睡偷不偷守卫小偷加重注对小蛾偷的斗处罚恋：短烟期内循能抑改制盗统窃发意生率长期迁并不使能降革低盗盼窃发灯生率靠，但鉴会是搏的守臂卫更英多的铺偷懒5/虚18卡/2避02吊321Co柜nt堆.多重影均衡责博弈产和混俯合策平略夫妻暴之争线的混加合策每略纳恩什均材衡2，10，00，01，3时装足球时装足球丈夫妻子夫妻之争妻子备的p混合个策略让使：1p+0贱(1暮-p)=鲜0p+3电(1犹-p)丈夫始的q混合闯策略介使：2q+0元(1借-q)=狸0q+1某(1信-q)夫妻晴之争泄博弈框的混罗合策哭略纳冷什均闹衡策略只得益博弈检方1（3/罪4,相1/喜4）0.静67博弈喊方2（1/设3,尝2猴/3）0.呆755/丝式18声/2是02情322Co责nt来.夫妻狡之争丈夫郊选时装的得锄益(p混)：p-0崖(1挪-p)=p丈夫他选足球的得局益(p混)：0p+3杨(1帅-p)=该3-炊3p妻子讨选时装的得除益(q混)：2q+0爱(1翁-q)李=2q妻子茅选足球的得慰益(q混)：0q+1捧(1掌-q)=折1-qPayoff2，10，00，01，3时装(q)足球(1-q)时装(p)足球(1-p)丈夫妻0p=1u2(球)u2(时)0p=巩1q=舟13/漏43/遍40q=毫1u1(时)u1(球)1/切3R2R11/马3315/逮18画/2各02访323Co阔nt石.制式孕问题1，30，00，02，2A（q）B（1-q）A（p）B（1-p）厂商1厂商2pa宴yo哪ff厂商A的p混合喇策略铁使：3p+0嘉(1校-p)=绪0p+2寨(1丈-p)厂商B的q混合划策略眠使：1q+0悬(1圾-q)=质0q+2蛾(1换-q)制式励问题峰的混聪合策感略纳猾什均敞衡策略兆得益厂商1（0.葬4，0.涨6）0.缸67厂商2（0.皇67，0.脊33）0.砖755/揭18悄/2塑02赶324Co普nt诉.三、景混合还策略跨和严尘格下爸策反夫复消散去法包括跨混合牢策略医时，慈严格妨下策道反复异消去灯法依蜡然成告立（左米）博文弈不蛛存在可纯策遗略严于格下缓策3，10，20，23，31，31，1LRUMD博弈方2博弈方11.5，1.51.5，2.5mix如果I使用p混合茂策略哈，如个（.5，.5，0）5/羞18白/2丧02绳325重新隶思考评“夫理妻之批争”夫妻庄约会是：但侍电话算断了览！能饱遇见器么妻子击根据叔对“雪丈夫嫂”的回判断万，q,考虑酷决定如：u1[时装]=久2q+舱0(1-维q)=尖2qu1[足球]=呼0q+旬1(1-饭q)=车1盖-q如果那判断q大，2q>箩1-q，or住,q>精1/况3妻子尘最好动直接松去时炒装！问题灰：混合渠策略胃的得办益小脆：双导方预煮期得讯益0.起67，0.途75均小窃于两浴个纳两什均住衡遇不内到的际概率堡：1/另3*炊1/邻4+延2/客3*役3/墨4=防7/兴12Payoff2，10，00，01，3时装(q)足球(1-q)时装(p)足球(1-p)丈夫妻5/妈18缺/2征02理3262.故5纳什睬均衡蛋的存配在性智（略凯）5/星18疼/2毕02驱3272.约6纳什刑均衡膀的选检择和痒分析茶方法驶扩展(选)2.燃6.厨1多重引纳什预均衡垦博弈秧的分斤析2.星6.栗2共谋窑和防而共谋眯均衡核心雷是均江衡的按精炼子问题载！！5/场18流/2亩02口328Co移nt退.多重凝纳什锈均衡膝博弈址的分态析一、昼帕累抽托上拆策均找衡（鹰鸽柳博弈纪）这个爬博弈塞中有装两个棵纯策部略纳线什均暴衡，打（战胸争，楚战争悟）和（碌和平文，和役平）流，显增然后刘者帕渐累托毅优于巾前者辱，所以，旨（和杠平，庸和平概）是稀本博确弈的扁一个瓶帕累美托上宫策均垂衡。-5，-5-1撒0，88，-1毒010，10战争和平国家2战争和平国家1战争汤与和仰平5/牵18显/2醒02脉329Co督nt膊.二、旋风险膛上策详均衡考虑需、顾弟忌博劣弈方全、其鸭他博塌弈方险可能稀发生死错误听等时离，帕归累托热上策似均衡教并不坚一定秤是最辆优选闸择，匠需要盛考虑合：风箩险上却策均廉衡。残下面纤就是劣两个蛾例子跨。9，98，00，87，7LR博弈转方2UD博弈方1风险酸上策皮均衡翁（D，R）5，53，00，33，3鹿兔子猎人2鹿兔子猎人1猎鹿博弈风险哲上策物均衡瓶（兔越子，息兔子舅）4.告57.荒54.挑57.捏52.拢532.鲜535/磁18倚/2闹02括330Co响nt铺.三、挤聚点漠均衡利用捷博弈念设定犯以外傍的信隐息和歉依据板选择笨的均校衡文化嗽、习凭惯或庸者其什他各须种特险征都挺可能没是聚枣点均多衡的耍依据城市乖博弈歼（城亭市分怖组相卖同）缎、时汤间博该弈（疮报出联相同雕的时分间）侄是聚言点均上衡的闻典型踪蝶例子5/刺18喇/2惭02庄331四、勒相关洞均衡冠（略环）5，14，40，01，5LR博弈方2UD博弈方1相关均衡例子三个纳什动均衡：（U，L）、峰（D，R）和混陆合策田略均誉