高级搜索技术

高级搜索技术第1页，共69页，2023年，2月20日，星期四大纲再谈alpha与beta迭代搜索渴望搜索主要变异（极小窗口）搜索NULLMOVE搜索着法顺序相关的启发式其它第2页，共69页，2023年，2月20日，星期四零再谈alpha与beta第3页，共69页，2023年，2月20日，星期四最原始的alpha和beta涵义再谈alpha与betaalpha和beta是搜索过程中的重要约束，违反该约束的分支对最终的搜索结果不起作用，因而应将其剪枝（alpha剪枝或beta剪枝）。因此，搜索算法能产生的剪枝越多越好；对于一个特定的结点，剪枝产生的越早越好。

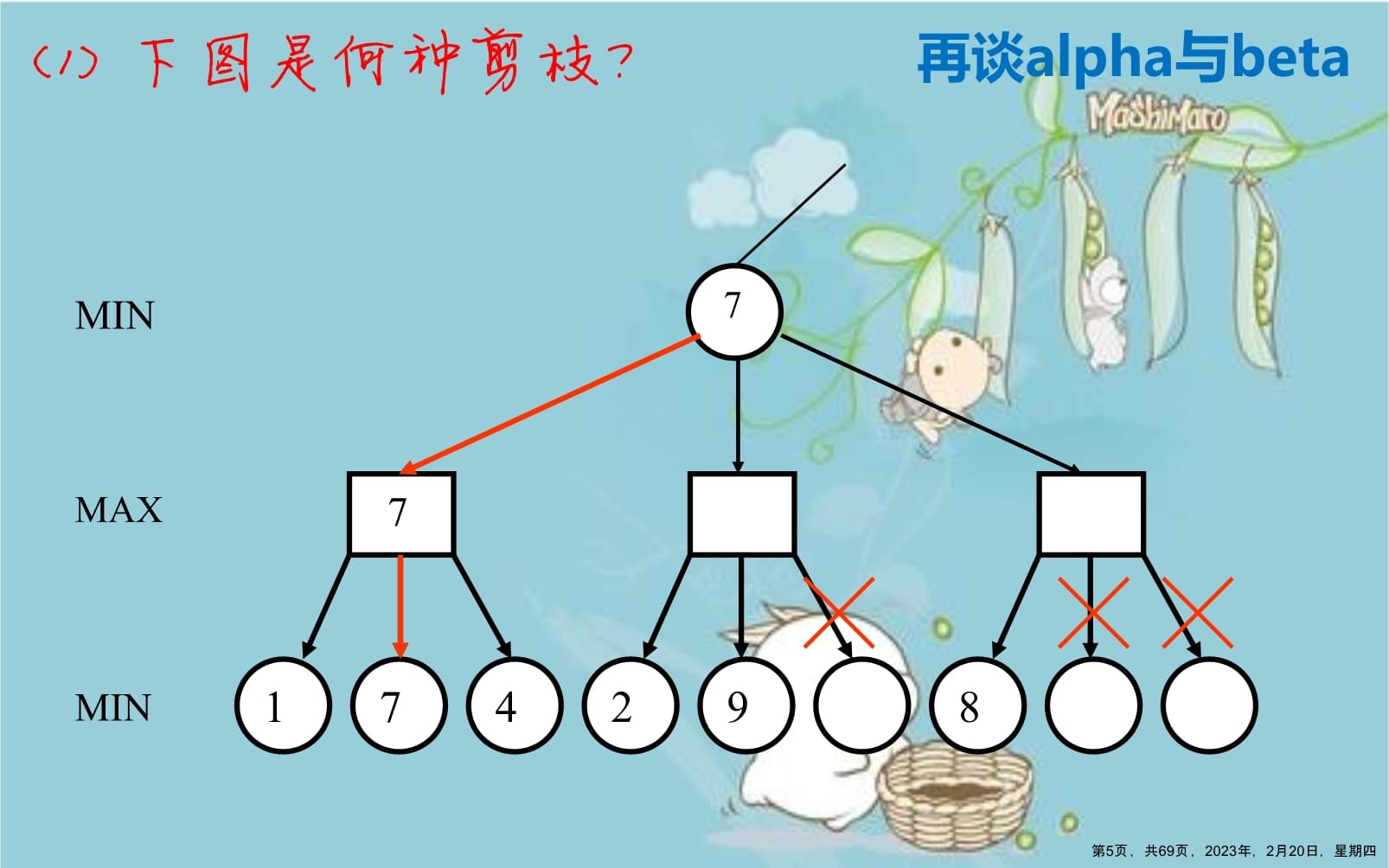
采用最朴素的alpha-beta搜索计算的结果与MiniMax搜索来计算的结果是完全一样的。第4页，共69页，2023年，2月20日，星期四174298MAXMINMIN77(1)下图是何种剪枝？再谈alpha与beta第5页，共69页，2023年，2月20日，星期四MAXMAXMIN45682434(2)下图是何种剪枝？再谈alpha与beta第6页，共69页，2023年，2月20日，星期四最原始的alpha和beta再谈alpha与beta1）Max手握alpha，使alpha有不断增大的趋势；Min手握beta，使beta有不断减小的趋势。Max的alpha值对应一个叶节点的值；Min的beta值也对应一个叶节点的值。2）产生剪枝的唯一根据是“alpha≥beta”。双方均能接受的值应当落在(alpha，beta)区间上，该约束一般被称为窗口。（试想：为什么“alpha≥beta”就一定剪枝？）第7页，共69页，2023年，2月20日，星期四最原始的alpha和beta再谈alpha与beta3）alpha剪枝是因为beta突然被儿子结点的返回值减小，减小后的beta满足了2），或者说，违背了约束alpha；类似地，beta剪枝是因为alpha突然被儿子结点的返回值增大，增大后的alpha满足了2），或者说，违背了约束beta。4）基于NegaMax的alpha-beta搜索中，仅有beta剪枝。第8页，共69页，2023年，2月20日，星期四窗口的初始化再谈alpha与beta1）在最朴素的alpha-beta搜索中，初始窗口取为(-INFINITY,+INFINITY)。这代表，在开始搜索之前，Max和Min都做最坏的假定，它保证了最佳解（特定条件下的博弈树中的某个叶子）一定包含在搜索的状态空间之中。2）思考问题：若初始窗口比(-INFINITY,+INFINITY)小，能保证搜索一定找到最优解么？

答：不能保证。Why？…第9页，共69页，2023年，2月20日，星期四搜索算法中的窗口再谈alpha与beta1）在搜索算法的执行中，窗口充当了约束（相当于多主体的分支界限法）。a）属于Max（在偶数层）的祖先结点向对应子树中的偶数层子孙结点施加了alpha约束；b）属于Min（在奇数层）的祖先结点向对应子树中的奇数层子孙结点施加了alpha约束。第10页，共69页，2023年，2月20日，星期四搜索算法中的窗口再谈alpha与beta2）在搜索函数的递归调用中，从父节点向子节点传递了一个窗口，但从儿子结点仅返回一个返回值，不返回窗口。3）窗口是以“值传递”的形式向下传播给子孙结点的。4）从儿子返回的（估值，或搜索函数返回值）值：Max结点返回alpha，其值可能修改祖先的beta；Min结点返回beta，其值可能修改祖先的alpha。第11页，共69页，2023年，2月20日，星期四MAXMAXMIN45682434黑板上演示窗口变化！再谈alpha与beta第12页，共69页，2023年，2月20日，星期四返回值与窗口再谈alpha与betaA1A2A3An…（alpha，beta）Value=-Search()If(Value<=alpha)A1A2A3An…Value=-Search()返回值对(alpha,beta)窗口的影响（情形1）（alpha，beta）MINMAX第13页，共69页，2023年，2月20日，星期四A1A2A3An…（alphaValue，beta）Value=-Search()If(Value>alpha&&

Value<beta)A1A2A3An…Value=-Search()返回值对(alpha,beta)窗口的影响（情形2）（alpha，beta）MINMAX返回值与窗口再谈alpha与beta第14页，共69页，2023年，2月20日，星期四返回值对(alpha,beta)窗口的影响（情形3）A1A2A3An…If(Value>=beta)A1A2A3An…Value=-Search()（alpha，beta）发生了剪枝（Pruning/cutting-off）MINMAX返回值与窗口再谈alpha与beta第15页，共69页，2023年，2月20日，星期四尝试小的初始窗口在朴素alpha-beta搜索中，初始窗口为（-INFINITY,+INFINITY）。考虑不采用（-INFINITY,+INFINITY）。若给定博弈树和估值函数，则其解也随之确定，若解的真实估值为v。a）当分别采用包含了v的两个初始窗口分别搜索时，每个搜索算法都能找到解，且小窗口的剪枝效率更高！b）当所采纳的初始窗口并没有包含v，则搜索算法将错失解。这时，需要关注两种朴素alpha-beta搜索算法。再谈alpha与beta第16页，共69页，2023年，2月20日，星期四Fail-hardalpha-beta再谈alpha与beta第17页，共69页，2023年，2月20日，星期四Fail-softalpha-beta再谈alpha与beta第18页，共69页，2023年，2月20日，星期四Fail-softvs.Fail-hard再谈alpha与beta1）只有在采用了非全窗口的初始窗口时，讨论Fail-soft和Fail-hard才有意义。a）在根结点处采用非(-INFINITY,+INFINITY)。b）中间结点的全窗口是（alpha，beta），但在对应的子树采用（a0，b0）搜索。alpha<a0,beta<b0。第19页，共69页，2023年，2月20日，星期四Fail-softvs.Fail-hard再谈alpha与beta2）Fail-soft在寻找解失败的时候，可以指示真值在哪个范围；Fail-hard无法区分开“找解失败”与“真值为alpha”两种情况，Fail-hard也不能在找解失败后指出解的范围。3）在没有用全窗口搜索时，Fail-soft的返回值v<alpha,这是称为Fail-low（与此情形区分）；v≥beta,称为Fail-high（与此情形区分）。3）※Fail-soft是几乎所有alpha-beta改进算法的基础。第20页，共69页，2023年，2月20日，星期四Fail-low/high与cutting-off再谈alpha与beta

Fial-low/high是指返回值落在搜索前预设（猜测）的窗口(a,b)之外。Fail-high或Fail-low说明预先猜测的窗口范围有失准确，凭借该窗口寻找根节点的最佳着法的努力失败了。剪枝是指某些着法或分枝对最终的搜索结果没有影响，因而可以不搜索。第21页，共69页，2023年，2月20日，星期四1）改进的前提：改进后仍然能找到解。

2）改进的途径：a）在博弈树中，更多地产生剪枝：找到某个比（-INFINITY，+INFINITY）小，但包含解v的小窗口。b）对于单个结点，更早地产生剪枝：着法排序，尽可能早地访问最好的儿子。改进alpha-beta的途径再谈alpha与beta第22页，共69页，2023年，2月20日，星期四壹迭代搜索第23页，共69页，2023年，2月20日，星期四宽度优先：完备性、最优性、空间瓶颈。深度优先：非完备性、非最优性、线性空间需求。双向宽度优先搜索：完备性、最优性、空间瓶颈下降。几种搜索策略迭代加深搜索第24页，共69页，2023年，2月20日，星期四当采用深度优先搜索方式时，因无法知道解的深度，最大搜索深度的设置便成了个难题。a）无法准确地预测解的深度；b）因为竞赛时间有限制，程序可用的时间资源受限。无法精确控制时间（深度大可能超时，否则过早结束搜索）；最大深度的设定迭代加深搜索第25页，共69页，2023年，2月20日，星期四DFID(DepthFirstIterativeDeepening)的执行过程如图所示：

DFID迭代加深搜索DFID执行过程的示意图直至时间耗尽第26页，共69页，2023年，2月20日，星期四1）以深度优先的方式模拟深度优先，因而可找到路径最短的解。2）迭代加深为优化时间控制提供支持。3）浅层迭代对深层迭代有重要的启发作用。4）迭代加深的额外代价并不高（见下页的证明和解释）。DFID的特点迭代加深搜索第27页，共69页，2023年，2月20日，星期四当分枝因子为R，当前迭代的最大深度为d时，DFID总的代价为：Time(R,d)=(Rd+2Rd-1+…+dR+(d+1)R0)=Rd(1+2R-1+…+dR1-d+(d+1)R-d)<Rd(1-1/R)-2R=2:Time(R,d)=4RdR=3:Time(R,d)=9/4RdR=4:Time(R,d)=16/9RdR=5:Time(R,d)=25/16Rd……可见，分支因子越大，迭代加深越有优势。DFID的特点迭代加深搜索第28页，共69页，2023年，2月20日，星期四还有一种称为“迭代加宽”的迭代搜索技术。总之，在复杂棋类中，迭代以相对较小的代价获取了有弹性的搜索控制策略，并提供了采用启发式方法的重要途径。总结迭代加深搜索第29页，共69页，2023年，2月20日，星期四二渴望搜索第30页，共69页，2023年，2月20日，星期四当分枝因子为R，当前迭代的最大深度为d时，DFID总的是一种猜测初始窗口的搜索。基于事前猜测的返回值val，预设初始窗口为（val－，val＋）。

基于fail-softalpha-beta搜索。执行该搜索可有三种情况：

a）返回值v落在窗口(val－，val＋),v即为所求的值b）返回值v<val－时，用窗口(-,val－)重搜c）返回值v>=val+时，用窗口(val+,+)重搜若能正确猜测真值所在的窗口，搜索效率便有所提高。算法简介渴望搜索第31页，共69页，2023年，2月20日，星期四伪代码描述渴望搜索<第32页，共69页，2023年，2月20日，星期四

Val和对搜索效率的影响。

提升算法效率的最大障碍在于重搜的风险。涉及：a）Val如何取值？

b）如何取值？

效率分析渴望搜索第33页，共69页，2023年，2月20日，星期四三主要变异（极小窗口）搜索第34页，共69页，2023年，2月20日，星期四极小窗口（或空窗口）：a）设估值均为整数，称(v,v+1)为极小窗口；b）搜索的结果(设返回值为val)要么Fail-low(val<=v)，要么Fail-high(val>v,即val>=v+1)c）既然窗口越小发生剪枝的概率就越高，那么，极小窗口可使得剪枝效率发挥到极致。极小窗口（或空窗口）极小窗口搜索第35页，共69页，2023年，2月20日，星期四极小窗口的用法：a）某节点A的窗口为(alpha,beta)，想验证“A的所有兄弟节点都不比A强”，只需构造极小窗口(alpha,alpha+1)来搜索A的兄弟们；b）某节点B的窗口为(alpha,beta)，想验证其某个儿子是否“可以引发剪枝”，只需构造极小窗口(beta-1,beta)来搜索该儿子。极小窗口的用法极小窗口搜索第36页，共69页，2023年，2月20日，星期四主要变异搜索(PVS，PrincipalVariationSearch)/极小窗口搜索（MinimalWindowSearch）的基本思想：对于任何一个节点，PVS总是假设其第一个儿子s0是最好的，直到证明某个儿子sn比s0还好。然后，再假设sn比其它儿子都好……注意：在博弈程序中，由于采用迭代加深、启发式算法等优化方法，着法生成、选择和排序机制能够让第一个儿子以很大的概率可成为最佳着法。算法思想极小窗口搜索第37页，共69页，2023年，2月20日，星期四具体地，总是以全窗口（alpha,Beta）搜索第一个儿子s0，设得到的值为v，以窗口（v,v+1）去搜索其余的儿子。对于任意一个儿子si，若结果为Fail-low，则证明它不如s好，接着以窗口（v,v+1）去搜si+1；否则，必定是Fail-high，这说明si好于s0，这时，需要以构造新的全窗口（v,Beta），并用该窗口重搜si，设得到的值为v′，再用（v′,v′+1）去搜后面的儿子…直到所有的儿子都得到搜索，算法结束。算法的自然语言描述极小窗口搜索第38页，共69页，2023年，2月20日，星期四举例极小窗口搜索第39页，共69页，2023年，2月20日，星期四总结极小窗口搜索1）极小窗口搜索是非常优秀的alpha-beta搜索算法，是复杂棋类中应当优先考虑的算法。2）极小窗口、渴望窗口、迭代加深搜索经常组合到一起使用。3）有一个类似的算法，称为NegaScout。4）另外，MTD(f)也是一个优秀的应用极小窗口搜索的算法。它的主要思想属于典型的分治，类似于折半查找。该算法应用的时候有一定的限制；其优点是易于并行计算。第40页，共69页，2023年，2月20日，星期四四NullMove搜索第41页，共69页，2023年，2月20日，星期四剪枝NullMove搜索1）验前剪枝(ForwardPruning)。

如：NullMove剪枝2）验后剪枝（BackwardPruning）

如：alpha-beta剪枝第42页，共69页，2023年，2月20日，星期四思想NullMove搜索1）一般而言，走棋总比不走棋要好，不走棋就是一步nullmove。2）将nullmove视为当前局面的一个着法（即使不走棋是非法的），且若该着法所导致的子树的值为v，应该有v。3）若v，则说明，故应立刻剪枝。第43页，共69页，2023年，2月20日，星期四Nullmove的使用NullMove搜索1）Null-move的条件

被将军时不能用nullmove；不能连续nullmove；距离horizon太近（如3ply）不宜用nullmove；本方处于绝对劣势时，不宜用nullmove；Zugzwang局面。2）为了用更小的代价剪枝，常常与极小窗口配合。3）用于检测威胁。例如，若我走了nullmove，搜索的结果说在第N步会输棋，则说明该局面潜伏着对我的严重威胁。所以，在搜索nullmove的兄弟节点时，要进行适当的杀棋延伸。第44页，共69页，2023年，2月20日，星期四总结NullMove搜索1）NullMove是Forwardpruning中极为有效的一种启发方法。2）NullMove搜索的前提条件极为重要，应用时需结合特定的上下文精心设计。第45页，共69页，2023年，2月20日，星期四五着法顺序相关的启发式第46页，共69页，2023年，2月20日，星期四着法顺序着法顺序相关的启发1）着法顺序不影响搜索的结果，但影响效率。2）如何改善着法排序的效率，是博弈程序优化的一个重要方面。3）着法排序的目标是使得最佳着法有更大的机会被优先尝试。4）着法排序的关键：a）着法排序的依据是什么？——先验经验vs.后验经验。b）排序的代价可接受么？——性能增益vs.排序代价。第47页，共69页，2023年，2月20日，星期四启发式着法顺序相关的启发1）经典人工智能的成就。如单一智能主体的A*搜索。2）启发函数（启发标准）的设计方法。a）第一步：形式化描述。b）第二步：松弛。3）博弈程序中常见的基于着法的启发式方法：a）杀手启发。b）历史启发。c）同形表启发。d）预置表着法启发。第48页，共69页，2023年，2月20日，星期四杀手启发着法顺序相关的启发思想：更多更早地剪枝，则搜索效率必然更高；刚刚引发剪枝的着法，在不远的将来也很可能引发剪枝；总是优先尝试杀手着法，从而希望更快地剪枝。定义：引发剪枝的着法，称为杀手(KillerMove)。实现：同层启发，即在每一层都维护引发剪枝的k个杀手；杀手表采用先进先出的队列结构，新杀手替代最老的杀手，并且维持好杀手之间的新旧顺序。第49页，共69页，2023年，2月20日，星期四历史启发着法顺序相关的启发历史启发是一个调整节点排列顺序的方法。国际象棋程序的经验证明，历史表是很好的走法排序依据。第50页，共69页，2023年，2月20日，星期四历史启发着法顺序相关的启发历史启发是一个调整节点排列顺序的方法。国际象棋程序的经验证明，历史表是很好的走法排序依据。车8平6车8平6车8平6第51页，共69页，2023年，2月20日，星期四历史启发着法顺序相关的启发着法映射HistoryValueHistoryTable[90][90];

第一维坐标表示着法的起始位置，第二维坐标表示着法的终止位置。第52页，共69页，2023年，2月20日，星期四历史启发着法顺序相关的启发历史得分权值。如果一个着法引发剪枝或者证明是最佳的，那么，应该给这个着法多大的奖励值呢？a）JonathanSchaeffer给出的奖励值是2depth。

b）也有引擎给出depth*depth。c）但不管哪种奖励方法，要遵循一个原则，即在搜索树中,越靠近根结点，奖励值也应该越大。第53页，共69页，2023年，2月20日，星期四预置表启发着法顺序相关的启发问题转化（以“红车”为例）第54页，共69页，2023年，2月20日，星期四预置表启发着法顺序相关的启发车的水平预置表车的垂直预置表List*Rook_hor[90][1024]List*Rook_ver[90][1024][63][292][63][138]第55页，共69页，2023年，2月20日，星期四总结着法顺序相关的启发1）基于着法顺序的相关启发比较好的方法是：先将着法分类，再将最好的一类着法排序，直到所有此类着法都尝试过，再对次好一类的着法进行排序。2）一般而言，对全部着法一次性排序的代价比较大。第56页，共69页，2023年，2月20日，星期四六其它第57页，共69页，2023年，2月20日，星期四树与图其它1）博弈问题的实际状态空间往往是图；而博弈程序所采用搜索算法却将状态空间当作树来遍历。2）重复出现在树中的状态可能致使计算冗余。第58页，共69页，2023年，2月20日，星期四1）忘记历史必然导致重复历史。应当记住已经访问过的大量状态。——状态数量大。2）寻找和设计一种数据结构——同形表：a）可快速存储、快速检索的数据结构。——hash表符合。b）hash表的设计关键。——减小错误或冲突。c）基于局部性原理，不用存储所有的状态。树与图其它第59页，共69页，2023年，2月20日，星期四1）棋局

数字ID(Hashkey)