材料力学例题

材料力学例题第1页/共128页0=CM=0AMABC①②1.75m2m2mP=25kNP=25kN1.75m2m2mABCO①②Dα1.75m2m2mABCO①②45°P=25kNN1’N2’EαN1’N2’P=25kN1.75m2m2mABCO①②45°Example:

如图的结构中，两杆的许用应力为160MPa。①

号杆由14号工字钢制成，而②号杆为圆形截面杆，校核

①

号杆的安全性，设计

②号杆的直径。第2页/共128页①

号杆的横截面积查表得21mm2152=A①

号杆中应力

①

号杆安全。在②号杆中，取d=30mmP=25kN1.75m2m2mABCO①②N1’P=25kN1.75m2m2mABCO①②N2’P=25kN1.75m2m2mABCO①②第3页/共128页bθlLAExample:

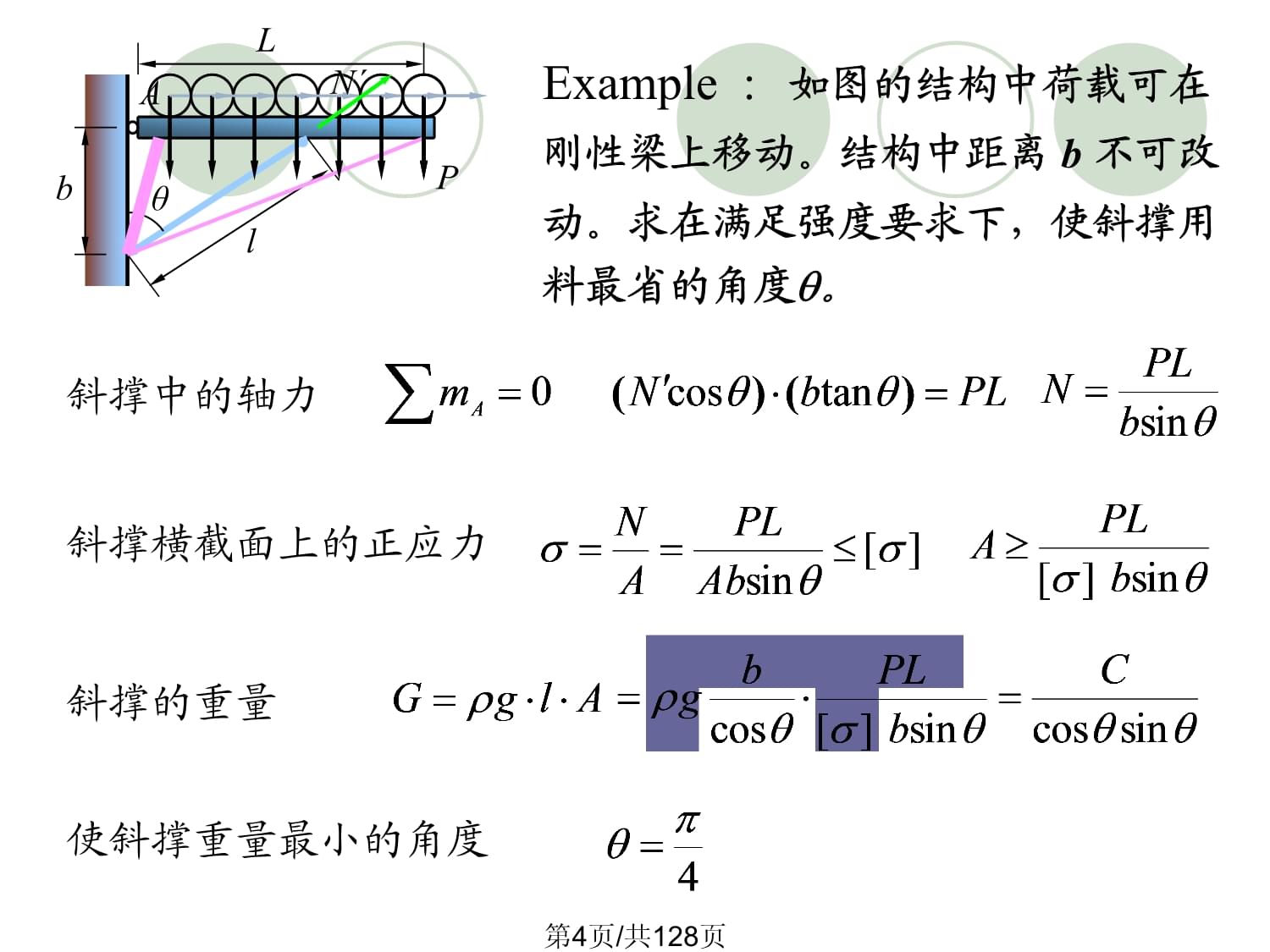
如图的结构中荷载可在刚性梁上移动。结构中距离

b不可改动。求在满足强度要求下，使斜撑用料最省的角度。斜撑中的轴力斜撑横截面上的正应力斜撑的重量使斜撑重量最小的角度PN´第4页/共128页Example:确定图示变截面柱体在强度充分发挥的情况下其横截面面积沿柱体轴线的变化规律,已知:P,,.xA(x)xlP解:xA(x)PN(x)W(1)求内力第5页/共128页(2)求应力(3)强度充分发挥时应有:等强度第6页/共128页xA(x)PN(x)W等强度柱体第7页/共128页Example:

在如图的结构中已知弹性模量E，求变截面杆的伸长量。建立如图的坐标系横截面高度横截面面积杆的伸长量h2h1bLFh2h1bLFxy第8页/共128页Example:

Determinetheaxialinternalforcesanddeformationofthebarshownfollows.Solve:(1)InternalforcesofthebarN(x)faLdf----frictionalforcesperunit

areaFxEA第9页/共128页N(x)FInthepartoutsideofthetube

LxNFa(2)Axialdeformationofthebar第10页/共128页A4.3

桁架结点位移计算PA45°aEAEAPA’A’ABCKS

在小变形情况下，可以用切线代替圆弧。第11页/共128页先求

CD杆内力由强度要求确定面积故取t=15mm由刚度要求确定面积Example:

如图的结构中，若CD杆总伸长不得超过0.65mm，试确定t。故应取tb=3t

[σ]=70MPaE=70GPaP=6kN0.6m0.8m0.1mABCD第12页/共128页平衡条件物理条件几何条件αE1A1E1A1PLE2A2N1N1N2αL

l1

l2(Equilibriumofforces)(Physicalequations)(Harminiousequations)第13页/共128页P力使BC段产生的变形量恰好为δ

时，平衡条件物理条件协调条件如果求解轴力构成超静定问题。如果

AB段无轴力产生。故有EAPL/2L/2δABCNBCEAPL/2L/2δABCNABNBCEAPL/2L/2δABCExample:

如图，弹性杆与刚性壁间有间隙

δ

，求

AB段的轴力。第14页/共128页Example:Determinethereactionofthecolumnatfixedendthatshwoninfollowsfigure.Thedensityofthematerialsis.TheYang’smodulusisEwhentensionandisE’whencompression.LSolve:(1)DeterminetheinternalforcesaTensioncompressionb第15页/共128页aTensioncompressionb压力拉力第16页/共128页(2)DeterminethereactionatthefixdendaTensioncompressionb压缩量拉伸量第17页/共128页协调方程第18页/共128页L第19页/共128页扭转第20页/共128页Solve:Example:Asolidshaftandahollowshaftaremadeofthesamematerialandareofthesameweightandlength.Ifthemaximumshearingstressisthesameineachshaft,theratiooftorqueswillbe:----istheratioofinternalradiusandexternalradiusofhollowshaft第21页/共128页第22页/共128页第23页/共128页㊀例如图的轴的许用切应力为60MPa，校核强度。若将实心圆轴改为内外径之比为0.7的空心圆轴，在强度相等的条件下，求两者的重量比。轴安全m1=1kNmm2

=3kNmD=60Tx1kNm2kNm第24页/共128页强度相等时两种轴

Wp

相等实心轴空心轴两者重量比取D1

为66mm例如图的轴的许用切应力为60MPa，校核强度。若将实心圆轴改为内外径之比为0.7的空心圆轴，在强度相等的条件下，求两者的重量比。第25页/共128页Example:Ashaftshownfollows,Determine:(1)theinternalforces.(2)maximumshearingstress.(3)Angleoftwistatarbitrarypoint.(4)Maximumangleoftwist.daa2aDCBAxSolve:(1)Internalforces第26页/共128页(2)Themaximumshearingstress

在

BC段轴的外缘(3)Angleoftwistatarbitrarypoint

第27页/共128页AB段:DCBAxBC段:第28页/共128页CD段:xaa2a(4)Maximumangleoftwist

第29页/共128页例

若[τ]=70MPa，求许用转矩。若端面

AB的相对转角与端面

BC相对转角相等，求

L1

。故许用扭矩

[T]=1.15kN·m故

L1

=298mmD=50L2L=510d2=38d1=25L1ABCB第30页/共128页记例图中铜套与钢轴紧密结合。若Gc和Gs已知，求铜套与钢轴中的最大切应力。mD

dSC平衡条件物理条件协调条件第31页/共128页Example:DeterminethereactionsoftheshaftatfixedendAandB.ABL/2L/2qdGSolve:一次超静定问题(1)InternalforcesABqC第32页/共128页(2)Harmoniousequation(3)ReactionatfixedendsABqC第33页/共128页弯曲第34页/共128页a/

2a/

2q㊀xQ3qa/8qa/83a/

89qa/12823qa/

8qa/

8xM例画出梁的剪力弯矩图。第35页/共128页Qxq2aa

qa2

㊀3a/

23qa/2-qa/2

qa2

9qa2/8qa/23qa/

2xM例画出梁的剪力弯矩图。第36页/共128页㊀xQ㊀aaqqa2qa/4-3qa/4-qa/42qa/32

23qa/42a/4qa/43qa/4Mx3分钟练习题:

画出梁的剪力弯矩图。第37页/共128页㊀㊀qaqa-qa/22q2qaaaxQMx例画出梁的剪力弯矩图。q2qaaa载荷对称梁Laodingssymetricalbeam剪力图反对称弯矩图对称第38页/共128页㊀xQqa2/8㊀aaqqqa/2-qa/2qa/2-qa2/8qa/2qa/2Mx例画出梁的剪力弯矩图。载荷反对称梁Loadingsanti-symetricalbeam剪力图对称弯矩图反对称第39页/共128页-㊀qaqaaaqa2/

2例画出梁的剪力弯矩图。2qaqa-qaxQxM-qa2/

2-qa2第40页/共128页㊀3kN/

m2m1m2kNm例画出梁的剪力弯矩图。3.25kN5.75kNxQ3.25kN-2.75kN3kNMx1.083m1.76kNm0.5kNm2kNm第41页/共128页㊀xM㊀Qxqaaqa

/2qa

/

2qa/2qa

/

2-qa/2qa2/2-qa/22qa/82先考虑右半部的平衡再考虑左半部的平衡qa

/2例画出带中间铰的梁的剪力弯矩图。第42页/共128页

两手握住直径2mm的钢丝两端使之微弯成圆弧形.如果圆弧的半径等于某个数值R,当两手不在用力时,钢丝不能恢复为直线形.已知材料的弹性模量为200GPa,屈服极限为320MPa,求R=?.

3分钟练习题第43页/共128页2m4mq=10kN/mP=10kN15kNExample:在如图的结构中，求最大拉应力和最大压应力。在B截面Qx15kN25kN10kN1.5m35kNIz

=

8.84106

mm4y1

=

45y2

=

90xM11.25kNm20kNmBA在A截面

最大拉应力在B

截面下边缘，数值为114.5MPa。最大压应力在A

截面下边缘，数值为203.6MPa。第44页/共128页两梁牢固粘合时两梁间无摩擦时，横截面上的弯矩由两梁均分。两种情况下弯矩相同PLhhb故Example:如图的梁由两根梁叠合而成，求两梁牢固粘合，或两梁光滑接触这两种情况下最大正应力之比。第45页/共128页Example:长度为

L的悬臂梁的横截面是边长为

a的正三角形。单位长度的重量为

q。仅由于自重，梁产生弯曲。该梁应如何放置，才能使梁中横截面上的最大正应力为最小？这个应力大小是多少？qLxCyCa

等边三角形对过形心的任一轴均为形心惯性主轴。xCyCa如图位置的ymax为最小。第46页/共128页5分钟练习题已知:求:abh解:梁为纯弯曲梁,有:因AB为水平线段,则只是简单拉伸,有:第47页/共128页

AB为均匀变形(与x

坐标无关),则有:第48页/共128页例试计算如图悬臂梁中最大正应力与最大切应力之比。

最大正应力产生在左端截面中上下两点

最大切应力产生在左端截面中性轴上两者之比lqd第49页/共128页2bbMx5kNm6.25kNm例已知如图梁的

[σ]为105MPa，试确定尺寸

b。故取b=45mm先确定危险截面：1m3m1mq=10kN/m第50页/共128页Example:

当

P至少为多大时，才可能使梁的根部与圆柱表面产生贴合？当

P

足够大，使梁己经与圆柱面贴合，试根据

P

决定贴合的长度。

至少应使梁根部挠曲线的曲率半径与R相同，才可能产生贴合。REIPLEIPLxCR第51页/共128页Example:Abeamisshownasfollows,determinetheslopeattheendAandthedeflectionatthemiddlepointC.Solve:(1)DeterminethereactionatfixedpinandtheaxialforceofthebarR=N=qL/2(2)DeterminethefunctionofbengingmomentinthebeamRM(x)Q(x)LxyL/2EAqABCEIRN第52页/共128页(3)Determinetheequationofdeflectioncurve(4)DeterminetheunknownconstantsCandDy(0)=0

boundaryconditions:D=0第53页/共128页Sothefunctionofslopeanddeflectionwillbe:(5)DeterminetheslopeatendAanddeflectionatmiddlepointC()()第54页/共128页Example:Asteplayercantileverbeamisshowninfollowsfiguer,determinethedeflectionattheendBandtheslopeatpointC.ABCyxL/2L/22EIEIFSolve:(1)Determinethefunctionsofbendingmoment(2)Determinethefunctionsofslopeanddeflectionofthebeam第55页/共128页(3)DeterminetheconstantsBoundaryconditions:Continuousconditions:第56页/共128页(4)DeterminethedeflectionattheendBandtheslopeatpointC.()()x第57页/共128页梁的转角和挠度与载荷及抗弯刚度之间的关系:转角集中力F均布载荷q挠度第58页/共128页Example:DeterminethedeflectionatpointDofthebeamshownfollows.qaDABCa/2a/2Solve:

Becausethethebeamisanti-symmetrical,wecanget:SothepartACofthebeamjustlikeasimplesupportedbeam.qDACa/2a/2()第59页/共128页Example:DeterminethedeflectionatthemiddlepointCofthebeamshownfollows.Solve:Theoriginalbeamcanbesuperpositionwithtwobeamsshownfollows.+BFABCFABCL/2L/2kAABCB’第60页/共128页Then:FABCL/2L/2kAFABCABCB’第61页/共128页LxyL/2EAqABCEIExample:ABL/2L/2+RN()Solve:q第62页/共128页Example:Solve:CRC+qCqCRqABCDL/2L/2aEI()()第63页/共128页aa/4EIAa/4Example:DeterminethedeflectionatthemiddlepointAofthebeamshownfollows.Solve:aa/4EIAa/4aa/4EIAa/4aa/4EIAa/4++第64页/共128页aa/4EIAa/4aa/4EIAa/4aa/4EIAa/4=第65页/共128页aa/4EIAa/4aa/4EIAa/4=第66页/共128页例求图示自由端的挠度。l/

2l/

2EIq0Al/

2l/

2θy

2y

3Bl/

2l/

2q0v

1lq0载荷的分解和重组

第67页/共128页例求图示自由端的挠度。l/

2l/

2EIq0Av1

1v2

2逐段刚化求解第68页/共128页例求图示自由端的挠度。l/

2l/

2EIq0Aq

0v3v1

1v2

2逐段刚化求解第69页/共128页例如图，无限长的梁放置在刚性平台上，梁单位长度重量为q，C处有作用力P=qa，求C处的挠度。aBCP

梁的变形如图。设平台上梁抬起的长度为

L，aCPAL

2分钟小练习:

梁抬起的长度

L?第70页/共128页例如图，无限长的梁放置在刚性平台上，梁单位长度重量为q，C处有作用力P=qa，求C处的挠度。qPL+aA

梁的力学模型可简化为左方固定端铰处弯矩为零的悬臂梁。aBCP

梁的变形如图。设平台上梁抬起的长度为

L，aCPAL第71页/共128页例

求

C点竖向位移

v。PLaABCPTTTTTφv2PPPPv1PPPPPv3第72页/共128页PLBAExample:DeterminethemaxiumlaodingwhenthemaxiumdeflectionofthebeamisnotoverL/300.PLBAPLBASolve:(1)Determinethereactions第73页/共128页(2)DeterminethemaxiumlaodingPLBAAccordingtothestiffnesscriteriawecanget:第74页/共128页qLB3qL/

8qL2/

85qL/

8qB例画出如图结构的剪力弯矩图。xQ3qL/

85qL/

8xMqL2/

89qL2/

128第75页/共128页例

画出如图结构的剪力弯矩图。左梁右梁协调条件故有RRQxqL/87qL/8xM3qL2/8qL2/8qL2/128LLqEI2EI7qL/83qL2

/8qL/8qL2

/8第76页/共128页aaEIEIEAaqACB例求图示A处的支反力,BC为刚性杆.协调条件B

处挠度C

处挠度EIqCREIABRACBvCvBAFmCBvBvC

设BC杆对简支梁的支撑力为R，

第77页/共128页A处支反力支反力偶矩问题:如果BC杆为变形杆，其抗拉刚度为EA,则会有什么样的结果?AFmCBvBvC第78页/共128页Example

：PP1P2MMTheconditionatthemiddlepointofthebeamis:L/

2L/

2PEICP1L/

2MCL/

2P2MC第79页/共128页最大挠度在悬臂梁的自由端处.P1L/

2MC第80页/共128页Example:Determinethereactionsatthefixedendsofthebeamshownfollows.ABCmLEISolve:Thebeamisaanti-symmetricalbeam

MmMRRACL/2MRBRML/2C第81页/共128页Theconditionsatthemiddleofthebeamare:ACL/2MR第82页/共128页FABCExample:Determinetheforceactedonthelowerbeem.Solve:BC’R(1)If(2)IfThisisastaticallyindeterminateproblemACRF第83页/共128页ACRFBC’R第84页/共128页组合变形第85页/共128页例求图中标明方向的切应力

τ。建立如图的坐标系斜截面法线方向应力状态分析1555τ455π/6xyπ/

31555τ

/

3455π

/6551545第86页/共128页例求如图应力状态的主应力和主方向。应力状态分析2010xy24.14.122.5°112.5°x´y´第87页/共128页例

某点应力状态是如图两种应力状态的合成。求该点的主应力。第二单元左侧面法向与x轴成15。第二单元上侧面法向与x轴成75。切向应力分量在这一方位上，第一个应力状态的法向应力分量151275°15xy在这一方位上，第一个应力状态的法向应力15xy15xy7.515xy7.51315xy7.51315xy7.5137.515xy7.5137.5第88页/共128页建立新坐标系，第一个应力状态在此坐标系中成为第二个应力状态在此坐标系中为两种应力状态的合成15xy7.5137.5151275°xy137.57.5y’x’第89页/共128页主应力:15xy7.5137.5151275°xy137.57.5y’x’0第90页/共128页例图示简支梁横截面为高度是

h、宽度是

b的矩形，已知材料的弹性模量E，泊松比。欲在轴线

K点处测出该点的最大拉应变，应变片应沿什么方向粘贴？应变片的理论读数是多少？

由于K点处于中性层上，因此该点处横截面上只有切应力而无正应力，故该点处于纯剪状态。K点所在横截面剪力：切应力：a2aFK第91页/共128页a2aFK

该点主应力沿45方向，应变片应沿这一方向粘贴。1345°主应力：主方向应变：第92页/共128页例如图单向拉伸杆中，已知E、v和A，若测得相互垂直方向上的线应变和，求P。由广义虎克定律第93页/共128页Example:AbarwasactedbyanaxialforcePshownfollows,knownEandvofthematerial,determinethetensionoflineAB.

PABSolve:bhCrosssectionWhereiswrong?第94页/共128页Example:AbarwasactedbyanaxialforcePshownfollows,knownEandvofthematerial,determinethetensionoflineAB.

PABSolve:bhCrosssection

SupposeCisanabtrarypointonthelineAB,itsstateofstresscanbeshowninthefollowsfigure.Acoordingtotheformulaof,wecanget:CxySimpletension第95页/共128页AcoorgingtothegeneralizedHook’slaw,followsresultcanbeattained.BecauseCisanabtrarypointonthelineAB,sothenormalstrainalongthelineABisuniform.Acoorgingtothedifinitionofnormalstrainwecanget:第96页/共128页ThetensionoflineABis:第97页/共128页Example:PointKwasonthesurfaceofashaftshowninfollowsfigure,knownE,vand,determinetheexternalmomentm.Thediameteroftheshaftisd.mmKSolve:

ThestatofstressatpointKispureshearing.xy第98页/共128页xyAcoordingtotheformulaof,wecanget:

AcoorgingtothegeneralizedHook’slaw,followsresultcanbeattained.第99页/共128页例图示一均质、等厚矩形板，承受一对集中载荷

P

，材料服从胡克定律，弹性模量

E与泊松比

μ均为已知。设板具有单位厚度，试求板的面积

A的改变量

ΔA

。aFFb以轴向为x方向，则有：面积改变量：第100页/共128页h=600b=800y=

40x=

80例对如图均匀变形的板，求：①厚度的改变量；②板面积的改变量；③体积的改变量。板中各方向上的应变第101页/共128页h=600b=800y=

40x=

80厚度的改变量板面积的改变量体积的改变量第102页/共128页例已知锅炉内径

D=1m，锅炉内部的蒸汽压强

p=3.6MPa，材料的许用应力

[σ]=160MPa，试用第四强度理论设计锅炉圆筒部份的壁厚

δ

。取δ=10mm径向轴向周向σ1σ2σ1δDp第103页/共128页例易拉罐的半径与厚度之比为200:1，材料的弹性模量为E=70GPa，ν=0.33，沿轴向的应变片在拉开罐时读数变化了170με，罐内的初始压力为多大？σaσc第104页/共128页δDp求:

薄壁圆筒表面上与轴线成45°方向上的应变片的读数.例已知:第105页/共128页Example:Determinethemaximumnormalstressofthebarshownfollows.h/2h/2bSolve:PPPPMABN=PM=Ph/4Thisproblemisacombineddeformationoftensionandbending.第106页/共128页h/2h/2bPPMABThedangeriouspointisB.Sowecanget:第107页/共128页

如图的集中荷载

P可在立柱端面中线上移动，要使立柱横截面上不产生拉应力，偏心量

e允许的最大值为多少？Example:Pehb第108页/共128页例如图的空心塔体由密度为

ρ

的材料制成。塔体侧面承受均布压力

q。为使塔体中横截面上不产生拉应力，塔上的重物P至少应为多大？最有可能产生拉应力的点在底部左侧点。该点压缩正应力最大弯曲正应力HPqρgAHDd第109页/共128页要不产生拉应力，应有HPqρgAHDd例如图的空心塔体由密度为

ρ

的材料制成。塔体侧面承受均布压力

q。为使塔体中横截面上不产生拉应力，塔上的重物P至少应为多大？第110页/共128页PM=PebP

ae630例如图偏心受拉杆件上侧和下侧分别测出应变，试求偏心距

e。GPa200=E10356×=-be101006×=-ae结构的偏心受拉构成拉弯组合第111页/共128页例

如图偏心受拉杆件上侧和下侧分别测出应变，试求偏心距

e。630GPa200=E10356×=-be101006×=-aebP

aePM=Pe第112页/共128页xyzqLLABdAB段承受弯扭组合变形最大弯矩扭矩故轴径d

应满足Example

:DeterminethediameterofbarABusingthefourthcriterion.Knowntheallowedstressofthematerial.第113页/共128页

结构中的弯矩如图，危险点在A点。A点应力故取h=90mm例

图示结构中，若材料

[σ+]为

80MPa，试确定横截面高度

h。Pz

=

2kNxyz600800Py

=

4kNAb=60h2.8kNm2.4kNmxyz第114页/共128页平移P1

到B，A截面承受弯扭组合荷载：平移P2

到B，A截面承受拉弯组合荷载：P1

=2kNP2

=3kNL=400mma=300mmd=50mm危险点应力状态扭转切应力xyzP2P1LaABdσNσMτP2xyzLABdP2

aP1xyzLaABdP1aP2P1xyzLaABdP2P1例

求图示结构

A截面危险点的第三强度相当