三角形的内切圆课件

三角形的内切圆1、确定一个圆的位置与大小的条件是什么？①.圆心与半径2、下图中△ABC与圆O的关系？△ABC是圆O的内接三角形；圆O是△ABC的外接圆圆心O点叫△ABC的外心知识回顾或②.不在同一直线上的三点ABCO

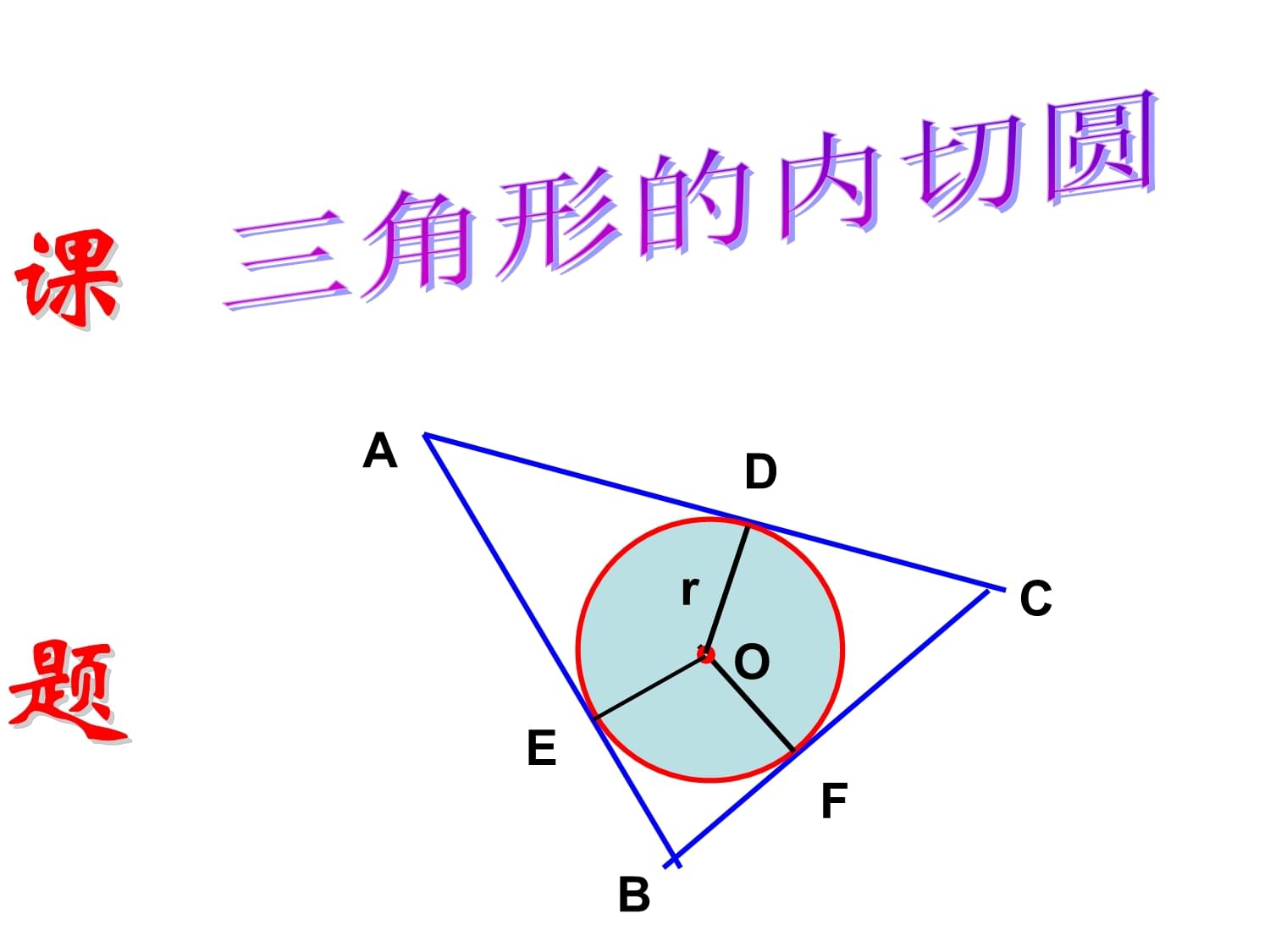
小明在一家木料厂上班，工作之余想对厂里的三角形废料进行加工：裁下一块圆形用料，且使圆的面积最大。下图是他的几种设计，请同学们帮他确定一下。思考ABC三角形的内切圆CBADFEOr课题思考下列问题：1．如图，若⊙O与∠ABC的两边相切，那么圆心O的位置有什么特点？圆心0在∠ABC的平分线上。

2．如图2，如果⊙O与△ABC的内角∠ABC的两边相切，且与内角∠ACB的两边也相切，那么此⊙O的圆心在什么位置？圆心0在∠ABC与∠ACB的两个角的角平分线的交点上。OMABCNO图2ABC合作探究：三角形内切圆的作法3．如何确定一个与三角形

三边都相切的圆的圆心位置

与半径的长？

4．你能作出几个与一个三角形的三边都相切的圆？内切圆圆心能否在三角形外部?

作出三个内角的平分线，三条内角平分线相交于一点，这点就是符合条件的圆心，过圆心作一边的垂线，垂线段的长是符合条件的半径。

IFCABED圆心都在三角形内部,因为三角形的三条内角平分线在三角形内部,且相交只有一个交点。

练习分别作出锐角三角形、直角三角形、钝角三角形的内切圆，并说明三角形的内心是否都在三角形内部．作法：ABC1、作∠B、∠C的平分线BM和CN，交点为I。

I2．过点I作ID⊥BC，垂足为D。3．以I为圆心，ID为半径作⊙I.⊙I就是所求的圆。

MND试一试,你能画出一个三角形的内切圆吗?每个学习小组请交流你们的画图方法1、定义：和三角形各边都相切的圆叫做三角形的内切圆，内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形。识记2、性质:内心到三角形三边的距离相等；内心与顶点连线平分内角。O图2ABC名称确定方法图形性质外心：三角形外接圆的圆心内心：三角形内切圆的圆心三角形三边中垂线的交点1.OA=OB=OC2.外心不一定在三角形的内部．三角形三条角平分线的交点1.到三边的距离相等；2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB3.内心在三角形内部．oABCOABC

例1.如图，△ABC中，O是内心，∠A的平分线和△ABC的外接圆相交于点D.求证：DO＝DB证明：连接BO，∵AD是∠BAC的平分线

∴

∠1=∠2，同理∠3=∠4，而∠BOD=∠1+∠3，

∠OBD=∠4+∠5，又∵∠2=∠5，∴∠BOD=∠OBD.∴DO=DB.例２、如图，已知⊙O是△ABC的内切圆，切点分别点D、E、F，设△ABC周长为Ｌ。求证：ＡＥ＋ＢＣ＝ＬOABCＦＥ想一想：常用辅助线及切线的性质DABCOcDEr如：直角三角形的两直角边分别是5cm，12cm则其内切圆的半径为______。知识的应用：如图，直角三角形的两直角边分别是a，b,斜边为c则其内切圆的半径ｒ为:（以含ａ、ｂ、ｃ的代数式表示ｒ）2cmr=a+b-c2

变式训练：Rt△ABC中,∠C=90º，AB等于5cm，内切圆半径为1cm，求这个三角形的周长？如图，设△ABC的边BC=a，CA=b,AB=c,s=(a+b+c),内切圆和各边分别相切于D,E,F

求证：AE=AF=s-a

BF=BD=s-b

CD=CE=s-cCBAEDFIr知识的应用圆内接平行四边形是矩形圆外切平行四边形是_______FACBD·O·