已阅读5页，还剩21页未读， 继续免费阅读
版权说明：本文档由用户提供并上传，收益归属内容提供方，若内容存在侵权，请进行举报或认领
文档简介
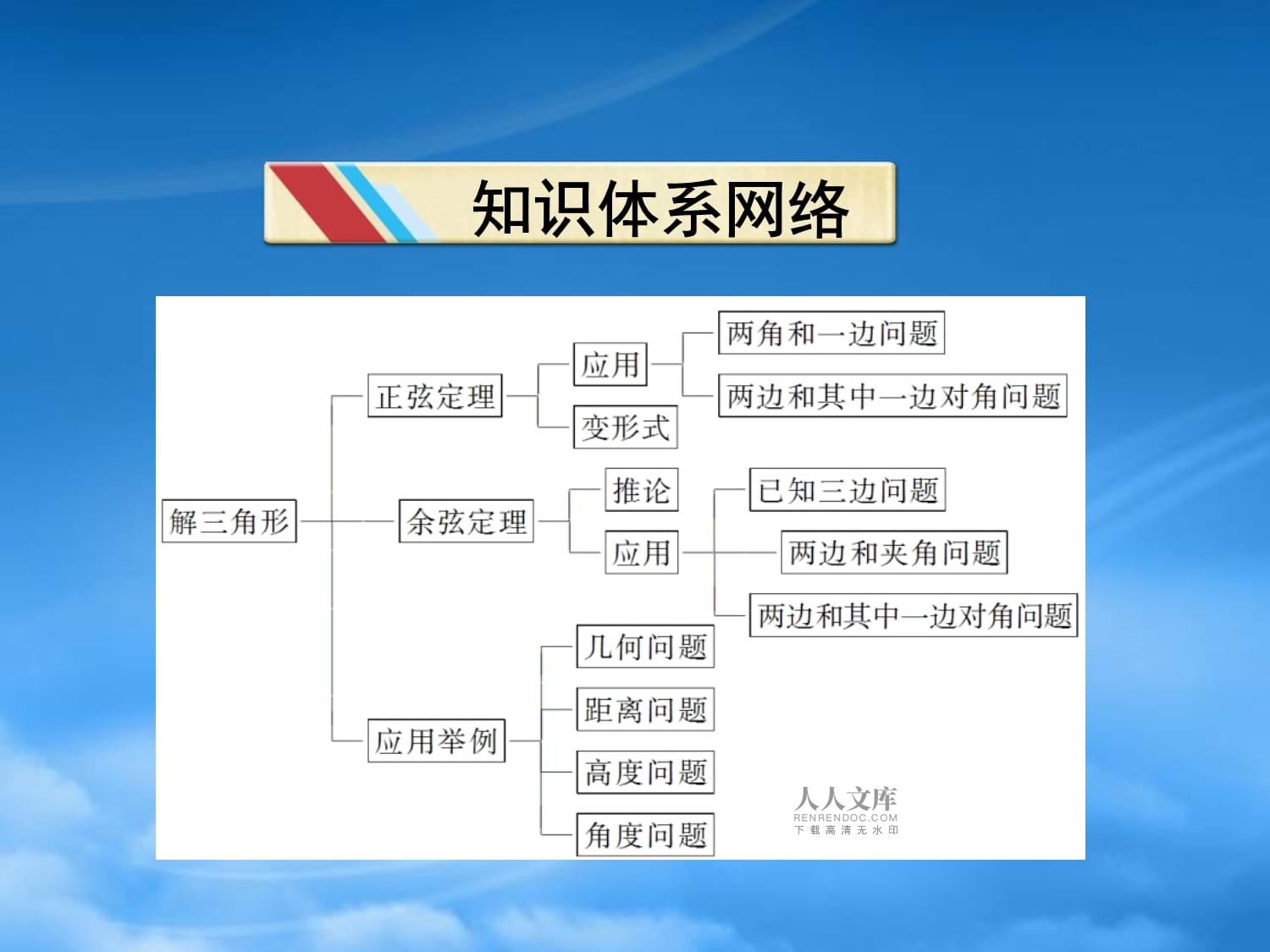
本章优化总结知识体系网络专题探究精讲专题一直接利用正余弦定理求解三角形值得注意的是已知三角形的任意两边与其中一边的对角，运用正弦定理解三角形时，解不确定，可结合三角形中大边对大角的性质去判断解的个数．余弦定理有两方面的应用：一是已知三角形的两边和它们的夹角，求第三边和其他两角；二是已知三角形的三边，求三个角．在初中已经学过的勾股定理，它是余弦定理的特例，而余弦定理又可看做是勾股定理的推广，应用中要注意，定理的变式要能够灵活应用．例1【分析】已知两边及其中一边的对角，用正、余弦定理均能解题．专题二三角形形状的判定例2【分析】转化为角或边之间的关系，进而判断．专题三正、余弦定理的综合应用例3【分析】由已知知条件件直接接应用用余弦弦定理理与正正弦定定理．．专题四解三角形在实际问题中的应用某人在在塔的的正东东沿着着南偏偏西60°°的方向向前进进40米以后后，望望见塔塔在东东北方方向，，若沿沿途测测得塔塔的最最大仰仰角为为30°°，求塔塔高．．【分析】构造出出三角角形，，用正正、余余弦定
温馨提示
- 1. 本站所有资源如无特殊说明，都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
- 2. 本站的文档不包含任何第三方提供的附件图纸等，如果需要附件，请联系上传者。文件的所有权益归上传用户所有。
- 3. 本站RAR压缩包中若带图纸，网页内容里面会有图纸预览，若没有图纸预览就没有图纸。
- 4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
- 5. 人人文库网仅提供信息存储空间，仅对用户上传内容的表现方式做保护处理，对用户上传分享的文档内容本身不做任何修改或编辑，并不能对任何下载内容负责。
- 6. 下载文件中如有侵权或不适当内容，请与我们联系，我们立即纠正。
- 7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。
最新文档
- 2024年c1驾照几2024年可以考客运资格证
- 2024年黔东南道路运输客运从业资格证模拟考试
- 2024年巢湖小型客运从业资格证考试题答案
- 2024年河北客运资格证考试题
- 2024年青海客运证模拟考试题库答案
- 2024年阜新考客运资格证试题题库软件
- 2024年辽宁客运驾驶从业资格考试题库及答案
- 2024年贵州客运从业资格证下载什么软件
- 项目管理（第四版）教案 专业优化年“改革深化年”活动的通知附件
- 市政工程设备租赁合同范本
- 汽车低压电线束技术条件
- 水稻常见病虫害ppt
- 学生会考核表(共3页)
- 小蛋壳历险记.ppt
- 六年级家长会家长代表演讲稿-PPT
- 学校校报校刊卷首语(创刊词)
- 《电容的连接》ppt课件
- 采集运维专业问答题(修订)20140627
- 毕业生就业推荐表填写说明-北京化工大学理学院.doc
- 一例重症肺炎的个案护理.doc
- 玻璃幕墙计算书
评论
0/150
提交评论