微分中值定理及其应用课件

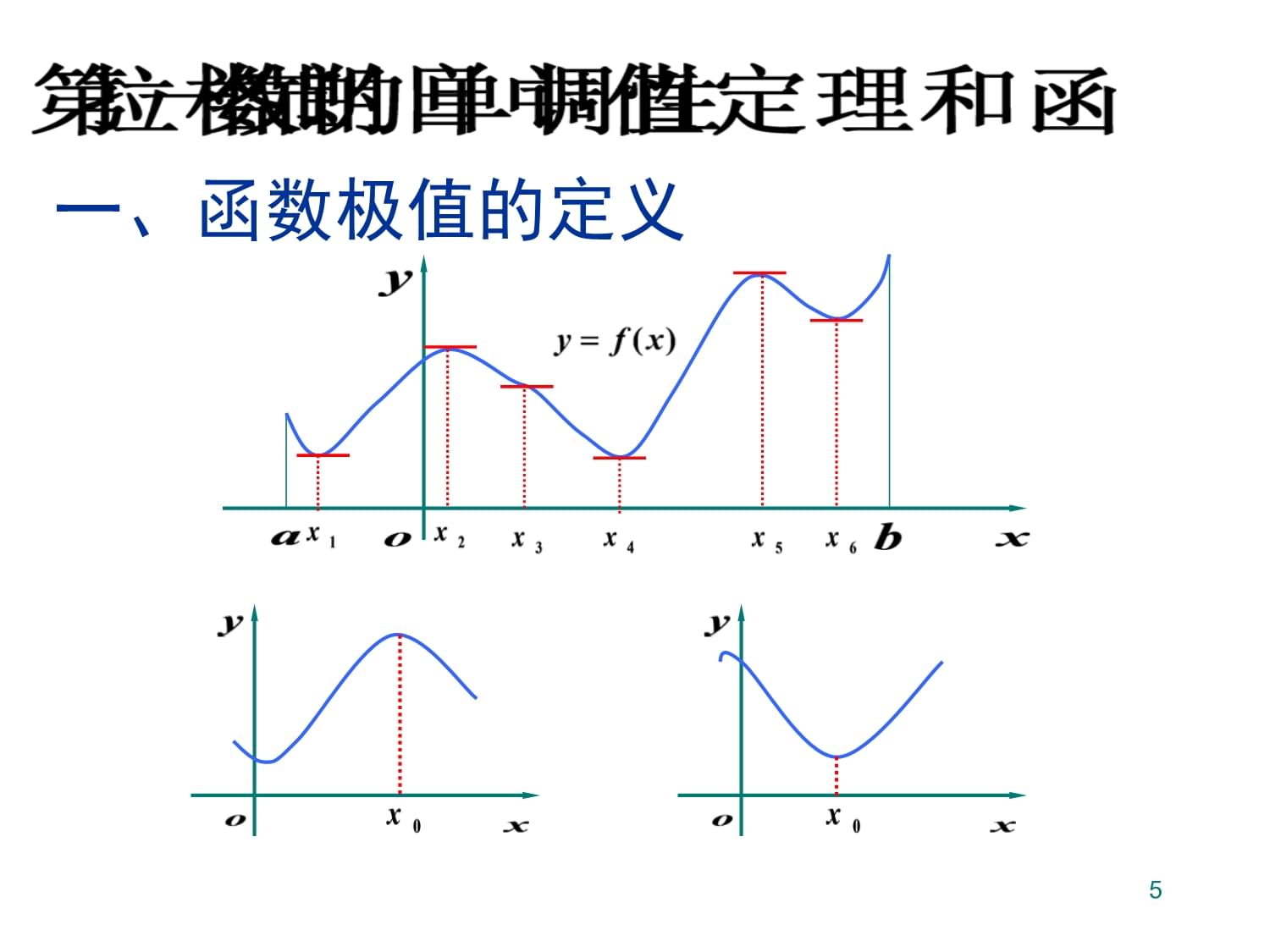
第六章微分中值定理及其应用一、罗尔(Rolle)定理二、拉格朗日(Lagrange)中值定理三、柯西(Cauchy)中值定理第六章微分中值定理及其应用一、罗尔(Rolle)定理1一、内容简介以罗尔定理，拉格朗日中值定理和柯西中值定理组成的一组中值定理是一整个微分学的理论基础，尤其是拉格朗日中值定理．它们建立了函数值与导数值之间的定量联系，因而可用中值定理通过导数去研究函数的性态；中值定理的主要作用在于理论分析和证明；同时由柯西中值定理还可导出一个求极限的洛必达法则．中值定理的应用主要是以中值定理为基础，应用导数判断函数上升、下降、取极值、凹形、凸形和拐点等项的重要性态。从而能把握住函数图象的各种几何特征．此外，极值问题有重要的实际应用．一、内容简介以罗尔定理，拉格朗日中值定理和柯西中值定理组成的2二、学习要求（1）理解和记忆罗尔定理、拉格朗日中值定理和柯西中值定理的条件和结论；（2）能正确运用洛必达法则求型、型等未定式的极限；（3）了解这三个中值定理在函数性态的研究当中所起的作用；（4）熟练地运用导数判定函数的增、减性和确定单调区间；（5）熟练地运用导数判定函数的凹、凸性和确定凹、凸区间；（6）用导数求出拐点；（7）熟练地用导数找到驻点及函数的极值；（8）能利用导数绘制函数图象；（9）能利用导数解决某些求最大、最小值的实际问题．二、学习要求（1）理解和记忆罗尔定理、拉格朗日中值定理和柯西3三、学习的重点与难点重点：拉格朗日中值定理、罗必达法则、函数性态（升降、极值、凹、凸、拐点）的判定，极值的实际应用问题。难点：运用中值定理的证明题，极值的应用题．三、学习的重点与难点重点：拉格朗日中值定理、罗必达法则、函数4一、函数极值的定义一、函数极值的定义5定义函数的极大值与极小值统称为极值,使函数取得极值的点称为极值点.定义函数的极大值与极小值统称为极值,使函数取得极值的点称为极6定理1(必要条件)定义注意:例如,这个结论又称为Fermat定理定理1(必要条件)定义注意:例如,这个结论又称为Fermat7MadebyHuilaiLi中值定理的演示T与l平行这样的x可能有好多MadebyHuilaiLi中值定理的演示T与l8●●这说明：在极大值或极小值点处,函数的导数为0.

几何意义是：在极值点处的切线平行于AB的连线或x轴.中值定理的演示典型情形的证明思想●结论:Rolle定理●●这说明：在极大值或极小值点处,函数的导数为0.9二、罗尔(Rolle)定理例如,二、罗尔(Rolle)定理例如,10注意:若罗尔定理的三个条件中有一个不满足,其结论可能不成立.例如,又例如,注意:若罗尔定理的三个条件中有一个不满足,其结论可能不成立.11点击图片任意处播放\暂停物理解释:变速直线运动在折返点处,瞬时速度等于零.几何解释:点击图片任意处播放\暂停物理解释:变速直线运动在折返点处,瞬微分中值定理及其应用课件13二、拉格朗日(Lagrange)中值定理二、拉格朗日(Lagrange)中值定理14MadebyHuilaiLiT与l平行中值定理的演示更广泛情形的证明思想:同一点MadebyHuilaiLiT与l平行中值定理的15作辅助函数拉格朗日中值公式注意:拉氏公式精确地表达了函数在一个区间上的增量与函数在这区间内某点处的导数之间的关系.作辅助函数拉格朗日中值公式注意:拉氏公式精确地表达了函数在一16拉格朗日中值定理又称有限增量定理.拉格朗日中值公式又称有限增量公式.微分中值定理拉格朗日中值定理又称有限增量定理.拉格朗日中值公式又称有限增17几何解释:几何解释:18微分中值定理及其应用课件19例1证例1证20例2证由上式得例2证由上式得21微分中值定理及其应用课件22导数介值定理又称达布（Darboux）定理导数介值定理又称达布（Darboux）定理23单调性的判别法定理单调性的判别法定理24微分中值定理及其应用课件25微分中值定理及其应用课件26定义:若函数在其定义域的某个区间内是单调的，则该区间称为函数的单调区间.导数等于零的点和不可导点，可能是单调区间的分界点．单调区间求法方法:定义:若函数在其定义域的某个区间内是单调的，则该区间称为函数27例4解单调区间为例4解单调区间为28例5解单调区间为例5解单调区间为29例6证注意:区间内个别点导数为零,不影响区间的单调性.例如,例6证注意:区间内个别点导数为零,不影响区间的单调性.例如,30第六章微分中值定理及其应用一、罗尔(Rolle)定理二、拉格朗日(Lagrange)中值定理三、柯西(Cauchy)中值定理第六章微分中值定理及其应用一、罗尔(Rolle)定理31一、内容简介以罗尔定理，拉格朗日中值定理和柯西中值定理组成的一组中值定理是一整个微分学的理论基础，尤其是拉格朗日中值定理．它们建立了函数值与导数值之间的定量联系，因而可用中值定理通过导数去研究函数的性态；中值定理的主要作用在于理论分析和证明；同时由柯西中值定理还可导出一个求极限的洛必达法则．中值定理的应用主要是以中值定理为基础，应用导数判断函数上升、下降、取极值、凹形、凸形和拐点等项的重要性态。从而能把握住函数图象的各种几何特征．此外，极值问题有重要的实际应用．一、内容简介以罗尔定理，拉格朗日中值定理和柯西中值定理组成的32二、学习要求（1）理解和记忆罗尔定理、拉格朗日中值定理和柯西中值定理的条件和结论；（2）能正确运用洛必达法则求型、型等未定式的极限；（3）了解这三个中值定理在函数性态的研究当中所起的作用；（4）熟练地运用导数判定函数的增、减性和确定单调区间；（5）熟练地运用导数判定函数的凹、凸性和确定凹、凸区间；（6）用导数求出拐点；（7）熟练地用导数找到驻点及函数的极值；（8）能利用导数绘制函数图象；（9）能利用导数解决某些求最大、最小值的实际问题．二、学习要求（1）理解和记忆罗尔定理、拉格朗日中值定理和柯西33三、学习的重点与难点重点：拉格朗日中值定理、罗必达法则、函数性态（升降、极值、凹、凸、拐点）的判定，极值的实际应用问题。难点：运用中值定理的证明题，极值的应用题．三、学习的重点与难点重点：拉格朗日中值定理、罗必达法则、函数34一、函数极值的定义一、函数极值的定义35定义函数的极大值与极小值统称为极值,使函数取得极值的点称为极值点.定义函数的极大值与极小值统称为极值,使函数取得极值的点称为极36定理1(必要条件)定义注意:例如,这个结论又称为Fermat定理定理1(必要条件)定义注意:例如,这个结论又称为Fermat37MadebyHuilaiLi中值定理的演示T与l平行这样的x可能有好多MadebyHuilaiLi中值定理的演示T与l38●●这说明：在极大值或极小值点处,函数的导数为0.

几何意义是：在极值点处的切线平行于AB的连线或x轴.中值定理的演示典型情形的证明思想●结论:Rolle定理●●这说明：在极大值或极小值点处,函数的导数为0.39二、罗尔(Rolle)定理例如,二、罗尔(Rolle)定理例如,40注意:若罗尔定理的三个条件中有一个不满足,其结论可能不成立.例如,又例如,注意:若罗尔定理的三个条件中有一个不满足,其结论可能不成立.41点击图片任意处播放\暂停物理解释:变速直线运动在折返点处,瞬时速度等于零.几何解释:点击图片任意处播放\暂停物理解释:变速直线运动在折返点处,瞬微分中值定理及其应用课件43二、拉格朗日(Lagrange)中值定理二、拉格朗日(Lagrange)中值定理44MadebyHuilaiLiT与l平行中值定理的演示更广泛情形的证明思想:同一点MadebyHuilaiLiT与l平行中值定理的45作辅助函数拉格朗日中值公式注意:拉氏公式精确地表达了函数在一个区间上的增量与函数在这区间内某点处的导数之间的关系.作辅助函数拉格朗日中值公式注意:拉氏公式精确地表达了函数在一46拉格朗日中值定理又称有限增量定理.拉格朗日中值公式又称有限增量公式.微分中值定理拉格朗日中值定理又称有限增量定理.拉格朗日中值公式又称有限增47几何解释:几何解释:48微分中值定理及其应用课件49例1证例1证50例2证由上式得例2证由上式得51微分中值定理及其应用课件52导数介值定理又称达布（Darboux）定理导数介值定理又称达布（Darboux）定理53单调性的判别法定理单调性的判别法定理54微分中值定理及其应用课件55微分中值定理及其应用课件56定义:若函数在其定义域的某个区间内是单调的