2020年北京初三数学第8课：全等三角形和相似三角形的再认识课件

全等三角形和相似三角形的再认识2020年海淀区空中课堂初三年级数学学科第8课全等三角形和相似三角形的再认识2020年海淀区空中课堂初三年观察这两组三角形，从图中看到了什么？想到了什么？全等三角形相似三角形观察这两组三角形，从图中看到了什么？想到了什么？全等三角形相

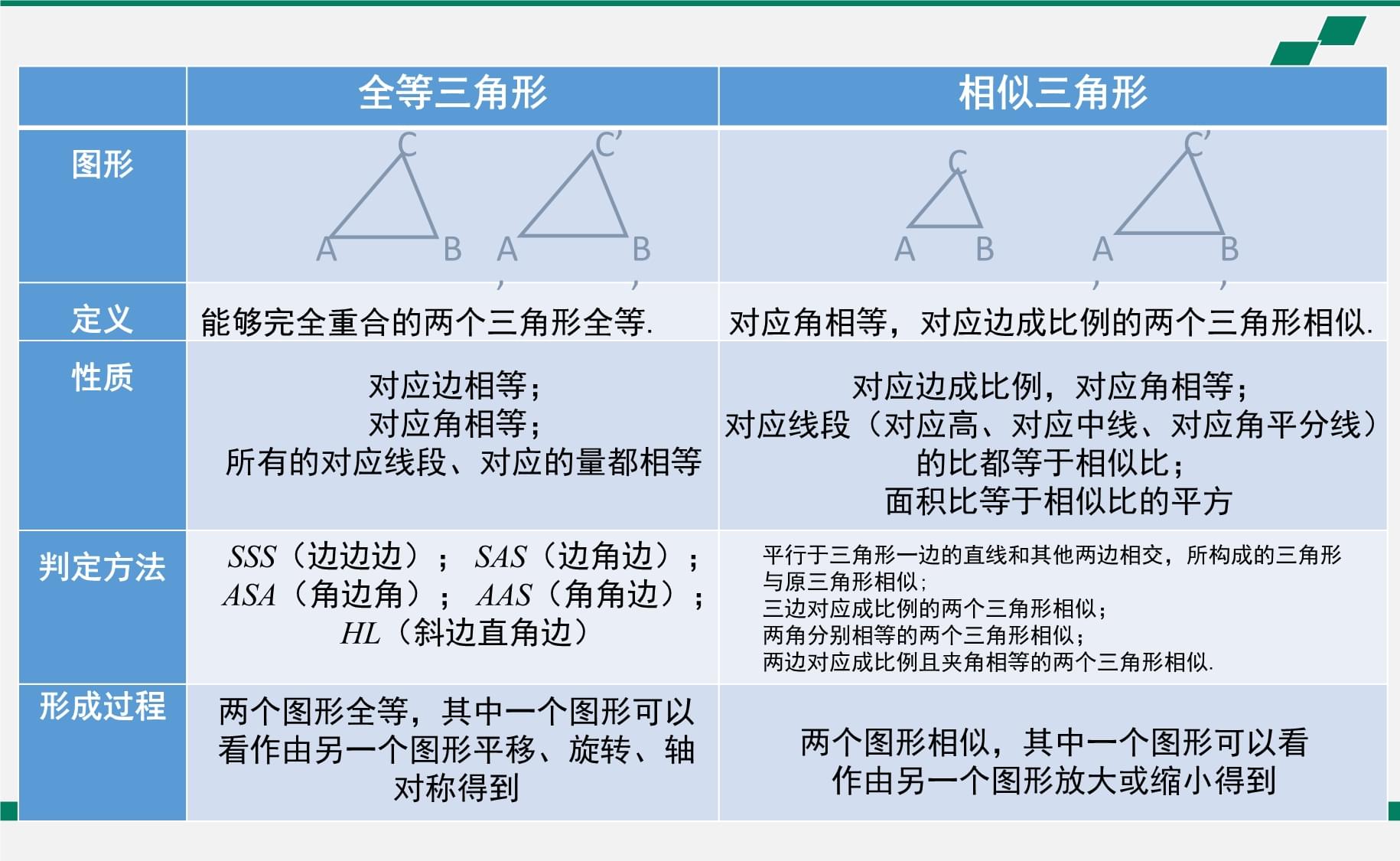
全等三角形相似三角形图形定义性质判定方法形成过程CABC’A’B’C’A’B’CAB能够完全重合的两个三角形全等.对应边相等；对应角相等；所有的对应线段、对应的量都相等SSS（边边边）；SAS（边角边）；ASA（角边角）；AAS（角角边）；HL（斜边直角边）两个图形全等，其中一个图形可以看作由另一个图形平移、旋转、轴对称得到对应角相等，对应边成比例的两个三角形相似.对应边成比例，对应角相等；对应线段（对应高、对应中线、对应角平分线）的比都等于相似比；面积比等于相似比的平方平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似;三边对应成比例的两个三角形相似；两角分别相等的两个三角形相似；两边对应成比例且夹角相等的两个三角形相似.两个图形相似，其中一个图形可以看作由另一个图形放大或缩小得到

全等三角形相似三角形图形定义性质判定方法形成过程CABC’从全等到相似——放大/缩小的数量关系与位置关系

特殊一般从全等到相似——放大/缩小的数量关系与位置关系

特殊一般例：如图，在锐角△ABC中，D是边AB的中点,

（1）过点D作直线，是否能得到全等三角形？请你写出作图方法，

并说出判定两三角形全等的依据.例：如图，在锐角△ABC中，D是边AB的中点,

（1）过点D例：如图，在锐角△ABC中，D是边AB的中点,（1）过点D作直线，是否能得到全等三角形？请你写出作图方法，

并说出判定两三角形全等的依据.解：①过点D作BC的平行线DE，再过点D作AC的平行线DF.例：如图，在锐角△ABC中，D是边AB的中点,解：例：如图，在锐角△ABC中，D是边AB的中点,（1）过点D作直线，是否能得到全等三角形？请你写出作图方法，

并说出判定两三角形全等的依据.解：①过点D作BC的平行线DE，再过点D作AC的平行线DF.△ADE≌△DBF.（ASA）例：如图，在锐角△ABC中，D是边AB的中点,解：△ADE≌例：如图，在锐角△ABC中，D是边AB的中点,（1）过点D作直线，是否能得到全等三角形？请你写出作图方法，

并说出判定两三角形全等的依据.解：①过点D作BC的平行线DE，再过点D作AC的平行线DF.△ADE≌△DBF.（ASA）②连接DC.例：如图，在锐角△ABC中，D是边AB的中点,解：△ADE≌例：如图，在锐角△ABC中，D是边AB的中点,（1）过点D作直线，是否能得到全等三角形？请你写出作图方法，

并说出判定两三角形全等的依据.解：①过点D作BC的平行线DE，再过点D作AC的平行线DF.△ADE≌△DBF.（ASA）②连接DC.△DEC≌△CFD.（ASA）例：如图，在锐角△ABC中，D是边AB的中点,解：△ADE≌例：如图，在锐角△ABC中，D是边AB的中点,（2）过点D作一条直线，是否能得到相似三角形？请你写出作图方法，并说出判定两三角形相似的依据.解：①过点D作BC的平行线DE；△ADE∽△ABC.

过点D作AC的平行线DF；△BDF∽△BAC.例：如图，在锐角△ABC中，D是边AB的中点,（2）过点D作例：如图，在锐角△ABC中，D是边AB的中点,（2）过点D作一条直线，是否能得到相似三角形？请你写出作图方法，并说出判定两三角形相似的依据.解：②作∠AE′D=∠B；△AE’D∽△ABC.△BDF’∽△BAC.作∠BDF′=∠C；例：如图，在锐角△ABC中，D是边AB的中点,（2）过点D作归纳：1、以上共有四对三角形相似，可以归为两类：一类为“正A”型；另一类为“斜A”型.“正A”型“斜A”型归纳：“正A”型“斜A”型归纳：2、判定两个三角形全等和相似的常规思路:判定两个三角形全等的常规思路判定两个三角形相似的常规思路1、若有两组角对应相等时，则需设法再找：①夹边对应相等(ASA)②其中任一组角的对边对应相等(AAS)2、若有两组边对应相等时，则需设法再找：①夹角对应相等(SAS)②第三边也对应相等(SSS)3、若有一边、一角对应相等时，

则需设法再找：4、在Rt△中,若有一组直角边对应相等时，则需设法再找：①夹等角的另一边也对应相等(SAS)②另一角也对应相等(AAS或ASA)①斜边对应相等(HL)②另一组直角边也对应相等(SAS)1、若有平行截线时：则用预备定理2、若有一组角对应相等时，则需设法再找：①另一组角也对应相等

②夹等角两边对应成比例3、若有两组边对应成比例时，则需设法再找：①夹角对应相等②第三边也对应成比例4、若有等腰关系时,则需设法再找：①顶角对应相等②其中一组底角对应相等③底和腰对应成比例归纳：判定两个三角形全等的常规思路判定两个三角形相似的常规思例：如图，在锐角△ABC中，D是边AB的中点,思考：若△ABC为等腰三角形（非等边），连接DC，是否有三角形相似？若没有，添加一个什么条件就存在三角形相似？例：如图，在锐角△ABC中，D是边AB的中点,思考：若△AB例：如图，在锐角△ABC中，D是边AB的中点,（3）若△ABC为等腰三角形（非等边），连接DC，是否有三角形相似？若没有，添加一个什么条件就存在三角形相似？分析：若△ABC为等腰三角形（非等边）时，（1）AB=AC（2）AB=BC（3）AC=BC例：如图，在锐角△ABC中，D是边AB的中点,（3）若△AB例：如图，在锐角△ABC中，D是边AB的中点,（3）若△ABC为等腰三角形（非等边），连接DC，是否有三角形相似？若没有，添加一个什么条件就存在三角形相似？分析：（1）当AB=AC时，①△ADC与△ABC：图中有△ADC、△BCD、△ABC共3个三角形∠A是公共角只需再寻找一组等角例：如图，在锐角△ABC中，D是边AB的中点,（3）若△AB例：如图，在锐角△ABC中，D是边AB的中点,（3）若△ABC为等腰三角形（非等边），连接DC，是否有三角形相似？若没有，添加一个什么条件就存在三角形相似？分析：（1）当AB=AC时，①△ADC与△ABC：图中有△ADC、△BCD、△ABC共3个三角形∠A是公共角若∠ADC=∠B只需再寻找一组等角例：如图，在锐角△ABC中，D是边AB的中点,（3）若△AB例：如图，在锐角△ABC中，D是边AB的中点,（3）若△ABC为等腰三角形（非等边），连接DC，是否有三角形相似？若没有，添加一个什么条件就存在三角形相似？分析：（1）当AB=AC时，①△ADC与△ABC：图中有△ADC、△BCD、△ABC共3个三角形∠A是公共角若∠ADC=∠B若∠ADC=∠ACB与外角性质矛盾！只需再寻找一组等角例：如图，在锐角△ABC中，D是边AB的中点,（3）若△AB例：如图，在锐角△ABC中，D是边AB的中点,（3）若△ABC为等腰三角形（非等边），连接DC，是否有三角形相似？若没有，添加一个什么条件就存在三角形相似？分析：（1）当AB=AC时，①△ADC与△ABC：图中有△ADC、△BCD、△ABC共3个三角形∠A是公共角若∠ADC=∠B若∠ADC=∠ACB与外角性质矛盾！且∠ACB=∠B只需再寻找一组等角∠ADC=∠B与外角性质矛盾！不相似！例：如图，在锐角△ABC中，D是边AB的中点,（3）若△AB例：如图，在锐角△ABC中，D是边AB的中点,（3）若△ABC为等腰三角形（非等边），连接DC，是否有三角形相似？若没有，添加一个什么条件就存在三角形相似？分析：（1）当AB=AC时，②△ADC与△BCD：不相似！如果△ADC与△BCD相似：例：如图，在锐角△ABC中，D是边AB的中点,（3）若△AB例：如图，在锐角△ABC中，D是边AB的中点,（3）若△ABC为等腰三角形（非等边），连接DC，是否有三角形相似？若没有，添加一个什么条件就存在三角形相似？分析：（1）当AB=AC时，②△ADC与△BCD若∠ADC=∠BDC如果△ADC与△BCD相似：若∠ADC=∠B若∠ADC=∠DCB与已知非等边矛盾！与外角性质矛盾！与外角性质矛盾！不相似！例：如图，在锐角△ABC中，D是边AB的中点,（3）若△AB例：如图，在锐角△ABC中，D是边AB的中点,（3）若△ABC为等腰三角形（非等边），连接DC，是否有三角形相似？若没有，添加一个什么条件就存在三角形相似？分析：（1）当AB=AC时，③△BCD与△BAC∠B是公共角从角的角度添加：从边的角度添加：∠BCD=∠A.∠BDC=∠ACB；∠BDC=∠B；“斜A”BC=CD；；；.相似！例：如图，在锐角△ABC中，D是边AB的中点,（3）若△AB例：如图，在锐角△ABC中，D是边AB的中点,（3）若△ABC为等腰三角形（非等边），连接DC，是否有三角形相似？若没有，添加一个什么条件就存在三角形相似？（1）当AB=AC时，①△ADC不可能与△ABC相似；②△ADC不可能与△BCD相似；③△BCD∽△BAC可以相似：（添加∠BDC=∠ACB或

∠BCD=∠A或BC=CD或

或等.）解：例：如图，在锐角△ABC中，D是边AB的中点,（3）若△AB例：如图，在锐角△ABC中，D是边AB的中点,（3）若△ABC为等腰三角形（非等边），连接DC，是否有三角形相似？若没有，添加一个什么条件就存在三角形相似？（2）当AB=BC时，分析：（1）分析：与（1）类似，因为这两种情况AB都是腰，点D都是腰AB的中点！例：如图，在锐角△ABC中，D是边AB的中点,（3）若△AB例：如图，在锐角△ABC中，D是边AB的中点,（3）若△ABC为等腰三角形（非等边），连接DC，是否有三角形相似？若没有，添加一个什么条件就存在三角形相似？（2）当AB=BC时，①△BCD不可能与△ABC相似；②△ADC不可能与△BCD相似；③△ACD∽△ABC：（添加∠ACD=∠B或∠ADC=∠ACB

或DC=AC或等.）解：与（1）类似例：如图，在锐角△ABC中，D是边AB的中点,（3）若△AB例：如图，在锐角△ABC中，D是边AB的中点,（3）若△ABC为等腰三角形（非等边），连接DC，是否有三角形相似？若没有，添加一个什么条件就存在三角形相似？（3）当AC=BC时，解：此时△ACD≌△BCD（SSS）所以△ACD∽△BCD.若添加一个条件∠ACB=90°:∠A=∠B=45°则△ACD∽△BCD∽△ABC.例：如图，在锐角△ABC中，D是边AB的中点,（3）若△AB回顾：判定两个三角形全等的常规思路判定两个三角形相似的常规思路1、若有两组角对应相等时，则需设法再找：①夹边对应相等(ASA)②其中任一角的对边对应相等(AAS)2、若有两组边对应相等时，则需设法再找：①夹角对应相等(SAS)②第三边也对应相等(SSS)3、若有一边、一角对应相等时，

则需设法再找：4、在Rt△中,若有一组直角边对应相等时，则需设法再找：①夹等角的另一边也对应相等(SAS)②另一个角也对应相等(AAS或ASA)①斜边对应相等(HL)②另一组直角边也对应相等(SAS)1、若有平行截线时：则用预备定理2、若有一组角对应相等时，则需设法再找：①另一组角也对应相等

②夹等角两边对应成比例3、若有两组边对应成比例时，则需设法再找：①夹角对应相等②第三边也对应成比例4、若有等腰关系时,则需设法再找：①顶角对应相等②其中一组底角对应相等③底和腰对应成比例先挖掘题目已知的边、角关系再根据判定方法找寻条件回顾：判定两个三角形全等的常规思路判定两个三角形相似的常规思从全等到相似从全等到相似从全等到相似从全等到相似从全等到相似从全等到相似从全等到相似从全等到相似从相似到全等从相似到全等全等图形和相似图形可以互相转化.全等图形和相似图形可以互相转化.作业：已知：在△ABE和△BCF中，若BA=BE，BC=BF，且∠ABE=∠FBC=α，取AF、CE的中点M、N，连接BM、BN、MN，

求证：BM=BN，∠MBN=α作业：已知：在△ABE和△BCF中，若BA=BE，BC=BF2.如图，在△ABC中，AD⊥BC于点D，BE⊥AC于点E，AD与BE交于点H，连接DE，找出此图中所有的相似三角形，并证明.

作业：2.如图，在△ABC中，AD⊥BC于点D，BE⊥AC于点E3.阅读理解：如图1，在直角梯形ABCD中，AB∥CD，∠B＝90°，点P在BC边上，当∠APD＝90°时，易证△ABP∽△PCD，从而得到BP•PC＝AB•CD，解答下列问题．（1）模型探究：如图2，在四边形ABCD中，点P在BC边上，当∠B＝∠C＝∠APD时，结论BP•PC＝AB•CD仍成立吗？试说明理由；（2）拓展应用：如图3，M为AB的中点，AE与BD交于点C，∠DME＝∠A＝∠B＝45°且DM交AC于F，ME交BC于G．AB＝

，AF＝3，求FG的长．作业：3.阅读理解：如图1，在直角梯形ABCD中，AB∥CD，∠B全等三角形和相似三角形的再认识2020年海淀区空中课堂初三年级数学学科第8课全等三角形和相似三角形的再认识2020年海淀区空中课堂初三年观察这两组三角形，从图中看到了什么？想到了什么？全等三角形相似三角形观察这两组三角形，从图中看到了什么？想到了什么？全等三角形相

全等三角形相似三角形图形定义性质判定方法形成过程CABC’A’B’C’A’B’CAB能够完全重合的两个三角形全等.对应边相等；对应角相等；所有的对应线段、对应的量都相等SSS（边边边）；SAS（边角边）；ASA（角边角）；AAS（角角边）；HL（斜边直角边）两个图形全等，其中一个图形可以看作由另一个图形平移、旋转、轴对称得到对应角相等，对应边成比例的两个三角形相似.对应边成比例，对应角相等；对应线段（对应高、对应中线、对应角平分线）的比都等于相似比；面积比等于相似比的平方平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似;三边对应成比例的两个三角形相似；两角分别相等的两个三角形相似；两边对应成比例且夹角相等的两个三角形相似.两个图形相似，其中一个图形可以看作由另一个图形放大或缩小得到

全等三角形相似三角形图形定义性质判定方法形成过程CABC’从全等到相似——放大/缩小的数量关系与位置关系

特殊一般从全等到相似——放大/缩小的数量关系与位置关系

特殊一般例：如图，在锐角△ABC中，D是边AB的中点,

（1）过点D作直线，是否能得到全等三角形？请你写出作图方法，

并说出判定两三角形全等的依据.例：如图，在锐角△ABC中，D是边AB的中点,

（1）过点D例：如图，在锐角△ABC中，D是边AB的中点,（1）过点D作直线，是否能得到全等三角形？请你写出作图方法，

并说出判定两三角形全等的依据.解：①过点D作BC的平行线DE，再过点D作AC的平行线DF.例：如图，在锐角△ABC中，D是边AB的中点,解：例：如图，在锐角△ABC中，D是边AB的中点,（1）过点D作直线，是否能得到全等三角形？请你写出作图方法，

并说出判定两三角形全等的依据.解：①过点D作BC的平行线DE，再过点D作AC的平行线DF.△ADE≌△DBF.（ASA）例：如图，在锐角△ABC中，D是边AB的中点,解：△ADE≌例：如图，在锐角△ABC中，D是边AB的中点,（1）过点D作直线，是否能得到全等三角形？请你写出作图方法，

并说出判定两三角形全等的依据.解：①过点D作BC的平行线DE，再过点D作AC的平行线DF.△ADE≌△DBF.（ASA）②连接DC.例：如图，在锐角△ABC中，D是边AB的中点,解：△ADE≌例：如图，在锐角△ABC中，D是边AB的中点,（1）过点D作直线，是否能得到全等三角形？请你写出作图方法，

并说出判定两三角形全等的依据.解：①过点D作BC的平行线DE，再过点D作AC的平行线DF.△ADE≌△DBF.（ASA）②连接DC.△DEC≌△CFD.（ASA）例：如图，在锐角△ABC中，D是边AB的中点,解：△ADE≌例：如图，在锐角△ABC中，D是边AB的中点,（2）过点D作一条直线，是否能得到相似三角形？请你写出作图方法，并说出判定两三角形相似的依据.解：①过点D作BC的平行线DE；△ADE∽△ABC.

过点D作AC的平行线DF；△BDF∽△BAC.例：如图，在锐角△ABC中，D是边AB的中点,（2）过点D作例：如图，在锐角△ABC中，D是边AB的中点,（2）过点D作一条直线，是否能得到相似三角形？请你写出作图方法，并说出判定两三角形相似的依据.解：②作∠AE′D=∠B；△AE’D∽△ABC.△BDF’∽△BAC.作∠BDF′=∠C；例：如图，在锐角△ABC中，D是边AB的中点,（2）过点D作归纳：1、以上共有四对三角形相似，可以归为两类：一类为“正A”型；另一类为“斜A”型.“正A”型“斜A”型归纳：“正A”型“斜A”型归纳：2、判定两个三角形全等和相似的常规思路:判定两个三角形全等的常规思路判定两个三角形相似的常规思路1、若有两组角对应相等时，则需设法再找：①夹边对应相等(ASA)②其中任一组角的对边对应相等(AAS)2、若有两组边对应相等时，则需设法再找：①夹角对应相等(SAS)②第三边也对应相等(SSS)3、若有一边、一角对应相等时，

则需设法再找：4、在Rt△中,若有一组直角边对应相等时，则需设法再找：①夹等角的另一边也对应相等(SAS)②另一角也对应相等(AAS或ASA)①斜边对应相等(HL)②另一组直角边也对应相等(SAS)1、若有平行截线时：则用预备定理2、若有一组角对应相等时，则需设法再找：①另一组角也对应相等

②夹等角两边对应成比例3、若有两组边对应成比例时，则需设法再找：①夹角对应相等②第三边也对应成比例4、若有等腰关系时,则需设法再找：①顶角对应相等②其中一组底角对应相等③底和腰对应成比例归纳：判定两个三角形全等的常规思路判定两个三角形相似的常规思例：如图，在锐角△ABC中，D是边AB的中点,思考：若△ABC为等腰三角形（非等边），连接DC，是否有三角形相似？若没有，添加一个什么条件就存在三角形相似？例：如图，在锐角△ABC中，D是边AB的中点,思考：若△AB例：如图，在锐角△ABC中，D是边AB的中点,（3）若△ABC为等腰三角形（非等边），连接DC，是否有三角形相似？若没有，添加一个什么条件就存在三角形相似？分析：若△ABC为等腰三角形（非等边）时，（1）AB=AC（2）AB=BC（3）AC=BC例：如图，在锐角△ABC中，D是边AB的中点,（3）若△AB例：如图，在锐角△ABC中，D是边AB的中点,（3）若△ABC为等腰三角形（非等边），连接DC，是否有三角形相似？若没有，添加一个什么条件就存在三角形相似？分析：（1）当AB=AC时，①△ADC与△ABC：图中有△ADC、△BCD、△ABC共3个三角形∠A是公共角只需再寻找一组等角例：如图，在锐角△ABC中，D是边AB的中点,（3）若△AB例：如图，在锐角△ABC中，D是边AB的中点,（3）若△ABC为等腰三角形（非等边），连接DC，是否有三角形相似？若没有，添加一个什么条件就存在三角形相似？分析：（1）当AB=AC时，①△ADC与△ABC：图中有△ADC、△BCD、△ABC共3个三角形∠A是公共角若∠ADC=∠B只需再寻找一组等角例：如图，在锐角△ABC中，D是边AB的中点,（3）若△AB例：如图，在锐角△ABC中，D是边AB的中点,（3）若△ABC为等腰三角形（非等边），连接DC，是否有三角形相似？若没有，添加一个什么条件就存在三角形相似？分析：（1）当AB=AC时，①△ADC与△ABC：图中有△ADC、△BCD、△ABC共3个三角形∠A是公共角若∠ADC=∠B若∠ADC=∠ACB与外角性质矛盾！只需再寻找一组等角例：如图，在锐角△ABC中，D是边AB的中点,（3）若△AB例：如图，在锐角△ABC中，D是边AB的中点,（3）若△ABC为等腰三角形（非等边），连接DC，是否有三角形相似？若没有，添加一个什么条件就存在三角形相似？分析：（1）当AB=AC时，①△ADC与△ABC：图中有△ADC、△BCD、△ABC共3个三角形∠A是公共角若∠ADC=∠B若∠ADC=∠ACB与外角性质矛盾！且∠ACB=∠B只需再寻找一组等角∠ADC=∠B与外角性质矛盾！不相似！例：如图，在锐角△ABC中，D是边AB的中点,（3）若△AB例：如图，在锐角△ABC中，D是边AB的中点,（3）若△ABC为等腰三角形（非等边），连接DC，是否有三角形相似？若没有，添加一个什么条件就存在三角形相似？分析：（1）当AB=AC时，②△ADC与△BCD：不相似！如果△ADC与△BCD相似：例：如图，在锐角△ABC中，D是边AB的中点,（3）若△AB例：如图，在锐角△ABC中，D是边AB的中点,（3）若△ABC为等腰三角形（非等边），连接DC，是否有三角形相似？若没有，添加一个什么条件就存在三角形相似？分析：（1）当AB=AC时，②△ADC与△BCD若∠ADC=∠BDC如果△ADC与△BCD相似：若∠ADC=∠B若∠ADC=∠DCB与已知非等边矛盾！与外角性质矛盾！与外角性质矛盾！不相似！例：如图，在锐角△ABC中，D是边AB的中点,（3）若△AB例：如图，在锐角△ABC中，D是边AB的中点,（3）若△ABC为等腰三角形（非等边），连接DC，是否有三角形相似？若没有，添加一个什么条件就存在三角形相似？分析：（1）当AB=AC时，③△BCD与△BAC∠B是公共角从角的角度添加：从边的角度添加：∠BCD=∠A.∠BDC=∠ACB；∠BDC=∠B；“斜A”BC=CD；；；.相似！例：如图，在锐角△ABC中，D是边AB的中点,（3）若△AB例：如图，在锐角△ABC中，D是边AB的中点,（3）若△ABC为等腰三角形（非等边），连接DC，是否有三角形相似？若没有，添加一个什么条件就存在三角形相似？（1）当AB=AC时，①△ADC不可能与△ABC相似；②△ADC不可能与△BCD相似；③△BCD∽△BAC可以相似：（添加∠BDC=∠ACB或

∠BCD=∠A或BC=CD或

或等.）解：例：如图，在锐角△ABC中，D是边AB的中点,（3）若△AB例：如图，在锐角△ABC中，D是边AB的中点,（3）若△ABC为等腰三角形（非等边），连接DC，是否有三角形相似？若没有，添加一个什么条件就存在三角形相似？（2）当AB=BC时，分析：（1）分析：与（1）类似，因为这两种情况AB都是腰，点D都是腰AB的中点！例：如图，在锐角△ABC中，D是边AB的中点,（3）若△AB例：如图，在锐角△ABC中，D是边AB的中点,（3）若△ABC为等腰三角形（非等边），连接DC，是否有三角形相似？若没有，添加一个什么条件就存在三角形相似？（2）当AB=BC时，①△BCD不可能与△ABC相似；②△ADC不可能与△BCD相似；③△ACD∽△ABC：（添加∠ACD=∠B或∠ADC=∠ACB

或DC=AC或等.）解：与（1）类似例：如图，在锐角△ABC中，D是边AB的中点,（3）若△AB例：如图，在锐角△ABC中，D是边AB的中点,（3）若△ABC为等腰三角形（非等边），连接DC，是否有三角形相似？若没有，添加一个什么条件就存在三角形相似？（3）当AC=BC时，解：此时△ACD≌△BCD（SSS）所以△ACD∽△BCD.若