《离散系统仿真基础》课件

3.离散系统仿真基础

离散事件动态系统(DEDS:DiscreteEventDynamicSystem)是指受事件驱动、系统状态跳跃式变化、系统状态迁移发生在一串离散时间点上的动态系统。整理课件3.离散系统仿真基础 离散事件动态系统(DEDS:Di1

3.1术语介绍系统——按照某些规律结合起来的，互相作 用、相互依存的所有元素的集合。实体——是对实际系统构成仿真模型所必须 的、不可略去的各种系统（元素）的抽象。（实体）属性——能描述该实体状态的一些量。它们可以是时间的函数，也可以不随时 间变化。系统状态——系统中全部实体的属性在某时刻t 所取量值的集合S(t)定义为“系统状态”。整理课件

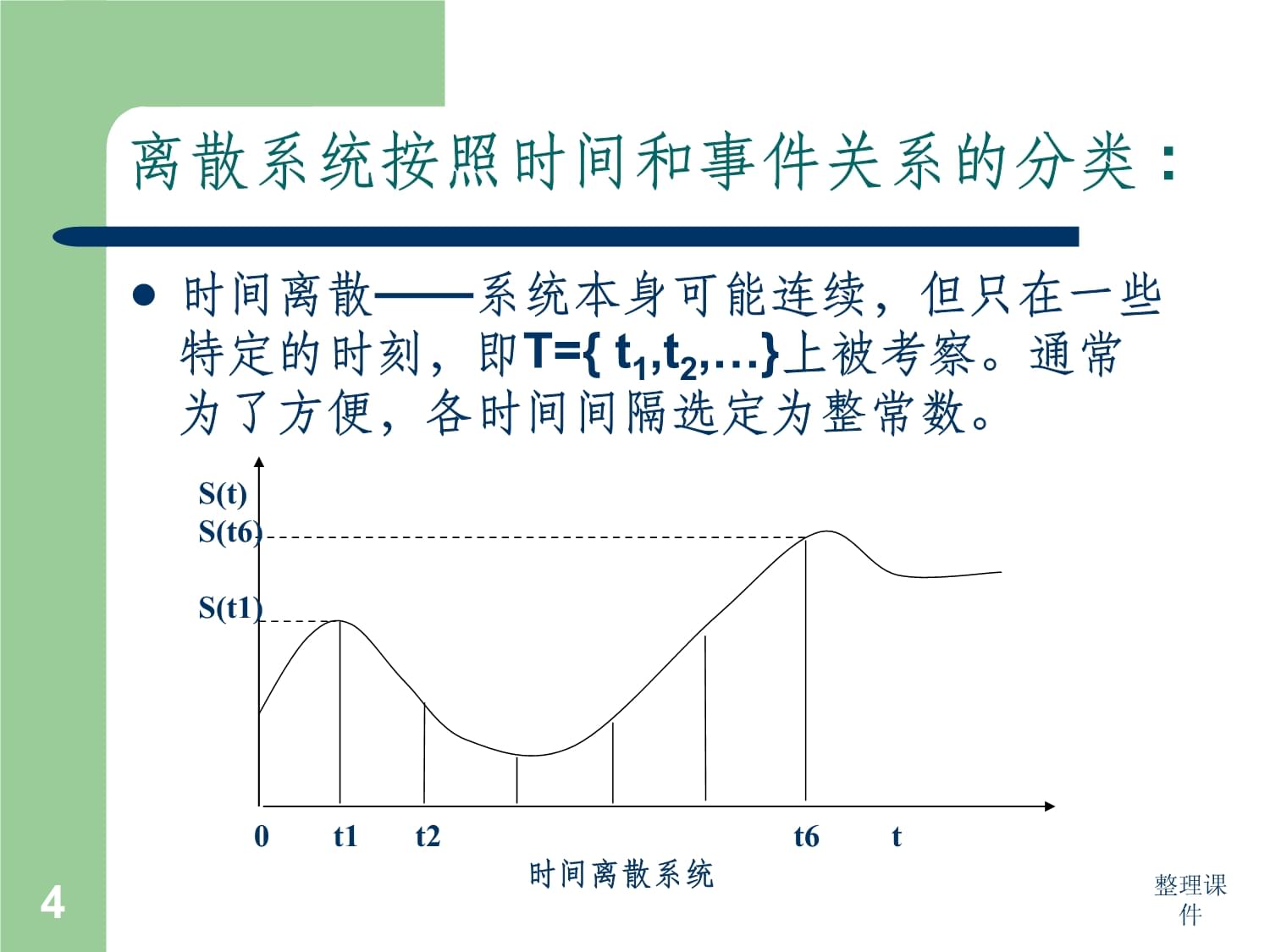
3.1术语介绍系统——按照某些规律结合起来的，互相作 2事件——当t在T上按某种序列{t1,t2,…}取值的过程中，系统状态发生了变化，就定义系统发生了某一“事件”。并把此时的ti值定义为“事件时刻”。活动——任何引起系统状态改变的过程称为“活动”。因此“活动”的结果使系统发生“事件”。而两个相邻“事件时刻”，可以看成是某一“活动”的过程。整理课件事件——当t在T上按某种序列{t1,t2,…}取值的过程中，3离散系统按照时间和事件关系的分类:时间离散——系统本身可能连续，但只在一些特定的时刻，即T={t1,t2,…}上被考察。通常为了方便，各时间间隔选定为整常数。S(t)S(t6)S(t1)0t1t2 t6t时间离散系统整理课件离散系统按照时间和事件关系的分类:时间离散——系统本身可能4时间连续而有离散事件——这时，系统状态的变化，即事件时刻是不连续的，跳跃式的。S(t)1（亮）0t1t2t3 t4t5t6t人工控制的红绿灯系统整理课件时间连续而有离散事件——这时，系统状态的变化，即事件时刻是不5离散系统例子系统实体属性事件急诊室护士，病床，医生，病人病情类型，护士和医生的服务速度，病人的发病类型和发病率病人到达，离院，护士检查结束，病人就诊银行出纳员，计算机，顾客帐户号，支票号，信用卡号，出纳员的服务速度，顾客到达率，存/取/其它操作出纳员服务，计算机查询，顾客到达，离去整理课件离散系统例子系统实体属性事件急诊室护士，病床，医生，病情类型6不同实体可以分成两类：静态实体——这类实体在系统中往往处于被动地位。它们为动态实体提供服务。因而起设备作用。描述这类实体的最常见的属性有：忙、闲、数量、地点、速度、设备号、服务时间等。动态实体——这类实体在系统中总是要求得到某些设备的服务。在系统的运行中，它们不断得以某种到达率“生成”。当从某一设备得到服务后，又流向其他设备以求服务。整理课件不同实体可以分成两类：静态实体——这类实体在系统中往往处于被7系统环境——能对系统产生影响的，属于系统 以外的元素集合。仿真目的——指仿真者希望通过仿真所获取系 统的哪些性能，信息。仿真模型——由系统数学模型根据仿真工具（语言）的特点，进行必要的结构变换，建立的合适算法。 对同一系统，仿真的目的不同，所建的模型也将不同。整理课件系统环境——能对系统产生影响的，属于系统 以外的元素集合。整83.2排队系统

在日常生活中，人们常常会见到各种各样的服务系统。例如：到食堂去买饭，炊事员和买饭人员构成一个服务系统；在公共汽车服务系统，由汽车、乘客和车站组成。服务系统的主要特征是出现排队。因此也称其为“排队系统”。整理课件3.2排队系统 在日常生活中，人们常常会见到各种各样的服9用于研究排队系统的理论基础是“排队论”

排队论最早由A.K.Erlang于1918年提出,在管理通讯和各类服务系统中有着广泛的应用,但是采用排队论方法来为DEDS建模服务却是近二十年来的事。以排队论为基础的网络模型是离散事件系统仿真中最常用的模型。整理课件用于研究排队系统的理论基础是“排队论” 排队论最早由A.10随机排队系统的三个组成部分：到达模式——指含个类型的动态实体按怎样的规律到达。服务机构——指同一时刻有多少服务设备可以接纳动态实体；对它们的服务需要多少时间。排队规则——到达的动态实体将按怎样的次序接受服务。整理课件随机排队系统的三个组成部分：到达模式——指含个类型的动态实11离散仿真要解决的基本问题

如何通过已知的到达模式和服务时间的概率分布，研究排队系统的队列长度和服务设备“忙”或“闲”的程度，就是离散仿真要解决的基本问题。

整理课件离散仿真要解决的基本问题 如何通过已知的到达模式和服务时间12几种常见的排队系统的结构：动态实体服务设备动态实体到达 离去 一线一服务设备排队系统结构动态实体服务设备1服务设备n动态实体到达 离去 ： ：

一线并联服务设备排队系统结构整理课件几种常见的排队系统的结构：动态实体服务设备动态实体到达 133.3到达模式确定型到达模式——顾客有规则地按照一定的间隔时间到达。泊松到达模式——满足4个条件平稳性：在[a,a+t]时间内有k个顾客到来的概率与a无关，只与t,k有关。记此概率为：Vk(t)——在t时间间隔内到达k个顾客的概率。(P(k,λt))无后效性：不相交区间内到达的顾客数是相互独立的。[t1,t2]到达数与[t0,t1]的到达数无关。普通性：令ψ(t)表示在长度为t的区间内至少到达两个顾客的概率，则ψ(t)=0当t->0；有限性：在任意有限时间区间内到达有限个顾客的概率之和为1。 整理课件3.3到达模式确定型到达模式——顾客有规则地按照一定的间隔14

其中λ>0为常数。令第i个顾客到达的时刻为τi(I=1,2,…)，τ1=0，且ti=τi-τi-1（i=1,2,…），则顾客相继到达的间隔t是相互独立相同分布的。其到达间隔的分布为指数分布。整理课件整理课件15指数分布：

泊松分布到达模式实际上是指：到达间隔时间为指数分布的到达模式。整理课件指数分布：整理课件16平均到达间隔时间Ta——在考虑模型的总时间 T中，共到达了n个“顾客”的情况下的比值 T/n。平均到达率λ——单位时间内到达的“顾客” 数。λ=1/Ta。到达间隔的分布函数A0(t)——到达间隔时间大 于t的概率。

整理课件平均到达间隔时间Ta——在考虑模型的总时间 T中，共到达了n17A0(t)1F(t)

A0(t)0 t整理课件整理课件183.2.2服务时间定长分布——这是最简单的情况。对每个动态实体的服务时间都是常数a，其分布函数为：指数分布——当服务时间完全是随机的情况，可以用指数分布来表示。其分布函数：整理课件3.2.2服务时间定长分布——这是最简单的情况。对每个动态19正态分布——在服务时间近似于常数的情况下，因多种随机因素的影响，使服务时间围绕这些常数值随机波动的情况。其中：σ>0，a——均值。F(x)记为：N(a,σ2)。当a=0，σ=1时，N(0,1)称为“标准正态分布”。整理课件正态分布——在服务时间近似于常数的情况下，因多种随机因素的影203.4排队规则和队列的度量排队规则——动态实体应依一定的次序和规则接受服务。损失制——动态实体到达时，如所有的服务设备均被占，则该实体就自动消失，永不再来。等待制——动态实体到达时，如所有的服务设备均被占，则它们就排成队伍，等待服务。服务次序可以采用下列各种规则：先到先服务先到后服务随机服务优先权服务整理课件3.4排队规则和队列的度量排队规则——动态实体应依一定的次21排队规则

在优先权服务时，必须考虑当一个比现在正接受服务的实体具有更高优先权级别的动态实体到达之后，系统将会做出怎样的处理：优先权仅决定动态实体的排队先后。立即停止当前服务，为新到的高优先权的实体服务。

整理课件排队规则 在优先权服务时，必须考虑当一个比现在正接受服务22排队规则3.混合制——队长有限制等待时间有限制逗留时间整理课件排队规则3.混合制——整理课件23队列的度量

设Ta为动态实体的平均到达间隔时间，λ=1/Ta为平均到达速度 Ts是设备的平均服务时间，μ=1/Ts是平均服务速度。定义：业务量强度——在已知平均到达速度λ和平均 服务速度μ，业务量强度： u=λ/μ=Ts/Ta设备利用率——得到服务的动态实体的到达速 率λ’与服务速度之比： ρ=λ’/μ整理课件队列的度量 设Ta为动态实体的平均到达间隔时间，λ=1/24对队列进行度量通常考察两个量：队列长度排队时间整理课件对队列进行度量通常考察两个量：队列长度整理课件253.5设备利用率和服务质量

对系统做假设：动态实体数量是无限的，其到达速率不受排队长度的影响，并且所到达的实体不会中途离去；到达模式为泊松分布，服务设备利用率ρ<1时，服务系统的动态实体平均数(L)为:服务时间为常数分布 L=ρ(2-ρ)/(2(1-ρ))服务时间为指数分布 L=ρ/(1-ρ)队列平均长度： Lw=1-ρ整理课件3.5设备利用率和服务质量 对系统做假设：动态实体数量26通过改变ρ来控制系统性能的方法：改变动态实体的到达速度改变服务设备的服务速度改变服务设备的数量整理课件通过改变ρ来控制系统性能的方法：改变动态实体的到达速度整理27系统的服务质量的衡量标准：能够立即得到服务的动态实体占到达实体总数的百分比。等待时间小于等于一个给定值T的动态实体占到达实体总数的百分比。用Pw(t)表示等待时间大于一时间长度(t)的概率。对泊松到达，指数服务的单服务设备系统有：

其中：t——指定的时间长度，ρ——设备利用率，μ平均服务速度。整理课件系统的服务质量的衡量标准：能够立即得到服务的动态实体占到达28例：对某个系统，平均服务时间为10秒，规定服务质量：在4个请求中至少有一个请求应立即给予响应而且等待时间超过30秒的请求不应超过请求总数的20%。分析：对第一个要求

Pw(0)=0.75=>ρ≤0.75 对第二个要求 如平均服务时间为10秒=>μ=1/10=0.1

整理课件例：对某个系统，平均服务时间为10秒，规定服务质量：整理课件29Pw(t)

1.00.8

ρ=0.80.6

ρ=0.60.4

ρ=0.40.2

ρ=0.2

0123456μt整理课件整理课件30

t=30秒=>μt=3。查曲线得Pw(3)≤0.2=>ρ≤0.6 如果用更小的利用率ρ，则会得到更低的概率。所以要求ρ≤0.6。综合两个要求，可取ρ≤0.6。为了使ρ=0.6就要求顾客的平均到达时间Ta=Ts/ρ=10/0.6=16.7（秒）。同样：对给定了到达间隔时间Ta时，也可求得Ts以达到满意的服务质量。

整理课件 t=30秒=>μt=3。查曲线得Pw(3)≤0.313.6排队系统建模（1）以排队论方法为基础的仿真模型设计技术主要适用于带时标的随机DEDS系统。 对排队系统来说，它只有两个基本的操作：“入队”和“离队”操作。排队模型的确切形式取决于服务设备的数量和排队线的数量。整理课件3.6排队系统建模（1）以排队论方法为基础的仿真模型设计技32开始对到达的动态实体做相关记录服务设备忙将实体挂在排队线上排队线长度加1设置服务设备为“忙”状态确定（此次）服务时间调度服务完成事件结束

Y N （时间）

入队操作

整理课件开始对到达的动态实体做相关记录服务设备忙将实体挂排队线长度加33设置服务设备为“空”状态排队线“空”按排队规则从队列中选出一个实体记录，让设备为它服务；累计等待时间确定（此次）服务时间；队列统计记录，队长度减1调度服务完成事件结束开始

Y N

离队操作整理课件设置服务设备为“空”状态排队线“空”按排队规则从队列中选出一34(2)Petri网络模型

Petri网模型最早在1962年CarlAdamPetri的博士论文中提出来，主要特性是具有较强的对并行、不确定性、异步和分布的描述能力和分析能力。 Petri网是一个模型化的工具，它是设想来用于模型化某一类问题：即有同时平行事件的离散事件的系统的问题。Petri网模型化了系统，特别是系统的两个方面（事件和条件）及它们之间的关系。整理课件(2)Petri网络模型整理课件35整理课件整理课件36整理课件整理课件37(3)有限状态自动机模型

离散事件系统自动机及形式语言理论最早是由P.J.Ramadge和W.M.Wonbarn等人八十年代中期提出的,现已成为DEDS研究的重要方法之一。 有限状态自动机模型描述方法主要适用于逻辑定性模型和无时标确定性模型的建模。建立有限状态自动机模型的关键是,基于适当的仿真策略选用相应状态集合,建立正确的转移关系函数和输出关系函数。整理课件(3)有限状态自动机模型整理课件384.离散事件仿真策略与结构模型

仿真过程的运行调度控制（特别是在用高级语言编程时），是通过所谓的“仿真策略”来实现的。 例：对一个含有一些出纳员，一些顾客和对应每个出纳员的银行（多）排队线的系统。 设：出纳员数量 5服务速度N(3,1) 顾客 到达 [0.2,0.8] 统计 队列长度（平均，最大，最小，方差） 出纳员利用率（平均，最大，最小，方差） 顾客在银行的时间（平均，最大，最小，方差）

整理课件4.离散事件仿真策略与结构模型 仿真过程的运行调度控制（39可以画出仿真程序的结构框图如下：预定仿真时间TIME=0预定第一个顾客到达时间开始TIME<仿真预定时间有顾客到达选择排队线将顾客插入排队线*调度下一个顾客的到达时间输出统计结果结束在这一段时间内有事务处理完（出纳空）顾客离去选择排队线上的顾客给予服务*调度为该顾客服务的完成时间TIME=TIME+1N

YN 到达事件 Y

N

Y整理课件可以画出仿真程序的结构框图如下：预定仿真时间开始TIME<仿40

这是种“面向时间”的时钟(TIME)处理。通过多次运行程序（试验）统计得到结果。程序每做一次循环，就增加一个时间单位。此时不论系统是否有时间发生，程序总是要查询系统状态，如发现没有时间发生就跳过该事件的处理程序。 这种方法的特点是：能和连续模型（进行时间离散）混合仿真。当事件子程序均能在一个时间单位内处理完成，则TIME的+1操作可以在机器硬件时钟的控制下执行，即仿真程序可以实时的（与机器时钟同步）运行。 缺点是：计算机做了很多不必要的空操作。因为在两个相邻事件时刻之间，系统没有活动需要计算机处理。目前很少使用此方法。 人们在研究了各种（离散）仿真调度方法的基础上，总结出三种通用的仿真策略，即：事件预定，活动扫描和进程互配。整理课件 这是种“面向时间”的时钟(TIME)处理。通过多次运行程414.1面向事件结构模型

面向事件结构模型是按事件独立预定策略组建成的。对上述的银行系统为例，其仿真程序结构框图：

整理课件4.1面向事件结构模型 面向事件结构模型是按事件独立预42TIME<仿真时间开始调度第一次到达事件从事件表中选出最先要执行的事件作为当前事件将时间TIME拨到当前事件的发生时刻按当前事件类型分支选择排队线将顾客插入该排队线调度下一次到达事件的产生时刻顾客离去选排队线上某顾客接受服务或“空闲”出纳员调度本次服务完成（时间）输出统计结果结束

产生第一个顾客到达，填入事件表

N Y到达事件 …… 事务完成整理课件TIME<仿真时间开始调度第一次到达事件从事件表中选出最先要43事件表结构：序号事件发生时间事件类型实体号:i100到达10i+1111接受服务8:k’201离去8k210到达11k+1整理课件事件表结构：序号事件发生时间事件类型实体号:i100到达1044面向事件结构模型

在这里，仿真时钟TIME是根据当前事件的发生时刻进行离散变化的。 “事件预定策略”强调：预定全部事件。事件将按显式调度。“事件功能”由事件程序实现。事件的调度是通过把事件按“事件标志”放在事件表中的方法来达到的。整理课件面向事件结构模型 在这里，仿真时钟TIME是根据当前事件的454.2活动扫描结构模型

当事件的发生不仅与时间有关，而且与其它条件也有关，即：只有在满足某些条件时发生。在这种情况下，由于活动持续时间的不确定性，无法预定活动的开始或终止时间。所以不易采用面向事件的结构模型。而活动扫描结构模型就是针对具有这种特点的系统的。整理课件4.2活动扫描结构模型 当事件的发生不仅与时间有关，而46活动扫描结构模型

活动扫描结构要求对事件隐式调度。在这里，状态的转换被表示成一组称之为“活动”的函数。 每次转换，由一个活动条件和一个动作组成。在每个（由预定事件生成时刻确定的）时间上，按某种（总体状态的）顺序扫描这些条件，如果出现一个条件是真，则立即执行与它联系的“动作”段；继续扫描，测试和执行，直到满足条件的活动都进行完。这是再按下一预定事件生成时刻向前推进模型的时钟。整理课件活动扫描结构模型 活动扫描结构要求对事件隐式调度。在这里，47活动扫描结构模型

按某种（总体状态）顺序扫描这些任务（包括检测小于当前时间应发生，但因条件未满足而延时发生的“以前”事件）。 在使用活动扫描策略时，需要借助事件预定策略进行时间（钟）管理。 事件预定策略不但要按预定事件的生成时刻向前推进仿真时钟，而且还按预定生成时刻激发事件（条件将在处理中测试）

整理课件活动扫描结构模型 按某种（总体状态）顺序扫描这些任务（包括48活动扫描表结构：序号事件发生时间事件类型实体号条件函数:i100到达10Ti+1111接受服务8F:k’201离去8Fk210到达11Tk+1整理课件活动扫描表结构：序号事件发生时间事件类型实体号条件函数:i1494.3进程互配模型结构

进程是一系列互相排斥的活动互配（在一个进程中，一次只能激活一个活动，进程中的活动间的连接关系：一个活动的结束，可以使该进程中的另一个活动的开始。不同的进程间会有重叠。（一个进程的活动需要取决于另一个进程中的活动的结束）。进程互配方法强调了这些进程之间的相互关系。整理课件4.3进程互配模型结构 进程是一系列互相排斥的活动互配50进程到达等待离去 事件：

顾客4 排队 服务 离去 等待 顾客3 排队 服务 到达 顾客2 服务 活动：

排队顾客1 服务 空闲 出纳2 空闲

空闲 忙 空闲 出纳1

E1E2E3E4E5E7E9E10时间（t） E6E8进程运行时间示意图整理课件进程整理课件51进程互配模型结构

面向进程的结构适用于处理结构的仿真模型。它的设计特点是：为每一个实体（如银行系统的顾客/出纳员）建立一个进程（一个运行程序），该进程的可能的活动将反映一个（动态）实体的建立开始到结束为止所经历的一条路径。由于顾客的到达、出纳员对事务处理的时间随机性，就会出现有多个进程并存于仿真程序中运行。（在E5，E6时刻有4个顾客的进程并存于系统） 在银行系统中，要建立的进程有两类：一类是动态实体——顾客，另一类是起设备作用的实体——出纳员。整理课件进程互配模型结构 面向进程的结构适用于处理结构的仿真模型。52顾客进程建立顾客对象确定下一个顾客的建立（到达）时间调度下一个顾客的活动（建立新顾客进程）出纳员“空闲”置出纳员“忙”确定服务时间调度服务完成（统计？）等待（中断进程）置出纳员“空闲”撤消（顾客）记录进程结束置“等待”标志（顾客）排队等待（中断进程）出纳员进程置出纳员“空闲”排队线空置出纳员为“空闲”从排队线上取出第一个顾客置出纳员为“忙”

初始化 初始化 Y NN Y排队 服务

死循环

挂起（中断进程，由进程调度启动）排队等待 服务等待 离去整理课件顾客进程建立顾客对象确定下一个顾客的建立（到达）时间调度下一53面向进程的结构，除了含有上述的进程部分之外，还有主程序及供主程序及各进程调用的标准子程序。总体结构如下：实体进程1实体进程2实体进程n公用子程序统计定时主程序初始化及说明启动全部（静态）实体进程启动一个或多个动态实体进程等待仿真的结束时间整理输出统计报告整理课件面向进程的结构，除了含有上述的进程部分之外，还有主程543.离散系统仿真基础

离散事件动态系统(DEDS:DiscreteEventDynamicSystem)是指受事件驱动、系统状态跳跃式变化、系统状态迁移发生在一串离散时间点上的动态系统。整理课件3.离散系统仿真基础 离散事件动态系统(DEDS:Di55

3.1术语介绍系统——按照某些规律结合起来的，互相作 用、相互依存的所有元素的集合。实体——是对实际系统构成仿真模型所必须 的、不可略去的各种系统（元素）的抽象。（实体）属性——能描述该实体状态的一些量。它们可以是时间的函数，也可以不随时 间变化。系统状态——系统中全部实体的属性在某时刻t 所取量值的集合S(t)定义为“系统状态”。整理课件

3.1术语介绍系统——按照某些规律结合起来的，互相作 56事件——当t在T上按某种序列{t1,t2,…}取值的过程中，系统状态发生了变化，就定义系统发生了某一“事件”。并把此时的ti值定义为“事件时刻”。活动——任何引起系统状态改变的过程称为“活动”。因此“活动”的结果使系统发生“事件”。而两个相邻“事件时刻”，可以看成是某一“活动”的过程。整理课件事件——当t在T上按某种序列{t1,t2,…}取值的过程中，57离散系统按照时间和事件关系的分类:时间离散——系统本身可能连续，但只在一些特定的时刻，即T={t1,t2,…}上被考察。通常为了方便，各时间间隔选定为整常数。S(t)S(t6)S(t1)0t1t2 t6t时间离散系统整理课件离散系统按照时间和事件关系的分类:时间离散——系统本身可能58时间连续而有离散事件——这时，系统状态的变化，即事件时刻是不连续的，跳跃式的。S(t)1（亮）0t1t2t3 t4t5t6t人工控制的红绿灯系统整理课件时间连续而有离散事件——这时，系统状态的变化，即事件时刻是不59离散系统例子系统实体属性事件急诊室护士，病床，医生，病人病情类型，护士和医生的服务速度，病人的发病类型和发病率病人到达，离院，护士检查结束，病人就诊银行出纳员，计算机，顾客帐户号，支票号，信用卡号，出纳员的服务速度，顾客到达率，存/取/其它操作出纳员服务，计算机查询，顾客到达，离去整理课件离散系统例子系统实体属性事件急诊室护士，病床，医生，病情类型60不同实体可以分成两类：静态实体——这类实体在系统中往往处于被动地位。它们为动态实体提供服务。因而起设备作用。描述这类实体的最常见的属性有：忙、闲、数量、地点、速度、设备号、服务时间等。动态实体——这类实体在系统中总是要求得到某些设备的服务。在系统的运行中，它们不断得以某种到达率“生成”。当从某一设备得到服务后，又流向其他设备以求服务。整理课件不同实体可以分成两类：静态实体——这类实体在系统中往往处于被61系统环境——能对系统产生影响的，属于系统 以外的元素集合。仿真目的——指仿真者希望通过仿真所获取系 统的哪些性能，信息。仿真模型——由系统数学模型根据仿真工具（语言）的特点，进行必要的结构变换，建立的合适算法。 对同一系统，仿真的目的不同，所建的模型也将不同。整理课件系统环境——能对系统产生影响的，属于系统 以外的元素集合。整623.2排队系统

在日常生活中，人们常常会见到各种各样的服务系统。例如：到食堂去买饭，炊事员和买饭人员构成一个服务系统；在公共汽车服务系统，由汽车、乘客和车站组成。服务系统的主要特征是出现排队。因此也称其为“排队系统”。整理课件3.2排队系统 在日常生活中，人们常常会见到各种各样的服63用于研究排队系统的理论基础是“排队论”

排队论最早由A.K.Erlang于1918年提出,在管理通讯和各类服务系统中有着广泛的应用,但是采用排队论方法来为DEDS建模服务却是近二十年来的事。以排队论为基础的网络模型是离散事件系统仿真中最常用的模型。整理课件用于研究排队系统的理论基础是“排队论” 排队论最早由A.64随机排队系统的三个组成部分：到达模式——指含个类型的动态实体按怎样的规律到达。服务机构——指同一时刻有多少服务设备可以接纳动态实体；对它们的服务需要多少时间。排队规则——到达的动态实体将按怎样的次序接受服务。整理课件随机排队系统的三个组成部分：到达模式——指含个类型的动态实65离散仿真要解决的基本问题

如何通过已知的到达模式和服务时间的概率分布，研究排队系统的队列长度和服务设备“忙”或“闲”的程度，就是离散仿真要解决的基本问题。

整理课件离散仿真要解决的基本问题 如何通过已知的到达模式和服务时间66几种常见的排队系统的结构：动态实体服务设备动态实体到达 离去 一线一服务设备排队系统结构动态实体服务设备1服务设备n动态实体到达 离去 ： ：

一线并联服务设备排队系统结构整理课件几种常见的排队系统的结构：动态实体服务设备动态实体到达 673.3到达模式确定型到达模式——顾客有规则地按照一定的间隔时间到达。泊松到达模式——满足4个条件平稳性：在[a,a+t]时间内有k个顾客到来的概率与a无关，只与t,k有关。记此概率为：Vk(t)——在t时间间隔内到达k个顾客的概率。(P(k,λt))无后效性：不相交区间内到达的顾客数是相互独立的。[t1,t2]到达数与[t0,t1]的到达数无关。普通性：令ψ(t)表示在长度为t的区间内至少到达两个顾客的概率，则ψ(t)=0当t->0；有限性：在任意有限时间区间内到达有限个顾客的概率之和为1。 整理课件3.3到达模式确定型到达模式——顾客有规则地按照一定的间隔68

其中λ>0为常数。令第i个顾客到达的时刻为τi(I=1,2,…)，τ1=0，且ti=τi-τi-1（i=1,2,…），则顾客相继到达的间隔t是相互独立相同分布的。其到达间隔的分布为指数分布。整理课件整理课件69指数分布：

泊松分布到达模式实际上是指：到达间隔时间为指数分布的到达模式。整理课件指数分布：整理课件70平均到达间隔时间Ta——在考虑模型的总时间 T中，共到达了n个“顾客”的情况下的比值 T/n。平均到达率λ——单位时间内到达的“顾客” 数。λ=1/Ta。到达间隔的分布函数A0(t)——到达间隔时间大 于t的概率。

整理课件平均到达间隔时间Ta——在考虑模型的总时间 T中，共到达了n71A0(t)1F(t)

A0(t)0 t整理课件整理课件723.2.2服务时间定长分布——这是最简单的情况。对每个动态实体的服务时间都是常数a，其分布函数为：指数分布——当服务时间完全是随机的情况，可以用指数分布来表示。其分布函数：整理课件3.2.2服务时间定长分布——这是最简单的情况。对每个动态73正态分布——在服务时间近似于常数的情况下，因多种随机因素的影响，使服务时间围绕这些常数值随机波动的情况。其中：σ>0，a——均值。F(x)记为：N(a,σ2)。当a=0，σ=1时，N(0,1)称为“标准正态分布”。整理课件正态分布——在服务时间近似于常数的情况下，因多种随机因素的影743.4排队规则和队列的度量排队规则——动态实体应依一定的次序和规则接受服务。损失制——动态实体到达时，如所有的服务设备均被占，则该实体就自动消失，永不再来。等待制——动态实体到达时，如所有的服务设备均被占，则它们就排成队伍，等待服务。服务次序可以采用下列各种规则：先到先服务先到后服务随机服务优先权服务整理课件3.4排队规则和队列的度量排队规则——动态实体应依一定的次75排队规则

在优先权服务时，必须考虑当一个比现在正接受服务的实体具有更高优先权级别的动态实体到达之后，系统将会做出怎样的处理：优先权仅决定动态实体的排队先后。立即停止当前服务，为新到的高优先权的实体服务。

整理课件排队规则 在优先权服务时，必须考虑当一个比现在正接受服务76排队规则3.混合制——队长有限制等待时间有限制逗留时间整理课件排队规则3.混合制——整理课件77队列的度量

设Ta为动态实体的平均到达间隔时间，λ=1/Ta为平均到达速度 Ts是设备的平均服务时间，μ=1/Ts是平均服务速度。定义：业务量强度——在已知平均到达速度λ和平均 服务速度μ，业务量强度： u=λ/μ=Ts/Ta设备利用率——得到服务的动态实体的到达速 率λ’与服务速度之比： ρ=λ’/μ整理课件队列的度量 设Ta为动态实体的平均到达间隔时间，λ=1/78对队列进行度量通常考察两个量：队列长度排队时间整理课件对队列进行度量通常考察两个量：队列长度整理课件793.5设备利用率和服务质量

对系统做假设：动态实体数量是无限的，其到达速率不受排队长度的影响，并且所到达的实体不会中途离去；到达模式为泊松分布，服务设备利用率ρ<1时，服务系统的动态实体平均数(L)为:服务时间为常数分布 L=ρ(2-ρ)/(2(1-ρ))服务时间为指数分布 L=ρ/(1-ρ)队列平均长度： Lw=1-ρ整理课件3.5设备利用率和服务质量 对系统做假设：动态实体数量80通过改变ρ来控制系统性能的方法：改变动态实体的到达速度改变服务设备的服务速度改变服务设备的数量整理课件通过改变ρ来控制系统性能的方法：改变动态实体的到达速度整理81系统的服务质量的衡量标准：能够立即得到服务的动态实体占到达实体总数的百分比。等待时间小于等于一个给定值T的动态实体占到达实体总数的百分比。用Pw(t)表示等待时间大于一时间长度(t)的概率。对泊松到达，指数服务的单服务设备系统有：

其中：t——指定的时间长度，ρ——设备利用率，μ平均服务速度。整理课件系统的服务质量的衡量标准：能够立即得到服务的动态实体占到达82例：对某个系统，平均服务时间为10秒，规定服务质量：在4个请求中至少有一个请求应立即给予响应而且等待时间超过30秒的请求不应超过请求总数的20%。分析：对第一个要求

Pw(0)=0.75=>ρ≤0.75 对第二个要求 如平均服务时间为10秒=>μ=1/10=0.1

整理课件例：对某个系统，平均服务时间为10秒，规定服务质量：整理课件83Pw(t)

1.00.8

ρ=0.80.6

ρ=0.60.4

ρ=0.40.2

ρ=0.2

0123456μt整理课件整理课件84

t=30秒=>μt=3。查曲线得Pw(3)≤0.2=>ρ≤0.6 如果用更小的利用率ρ，则会得到更低的概率。所以要求ρ≤0.6。综合两个要求，可取ρ≤0.6。为了使ρ=0.6就要求顾客的平均到达时间Ta=Ts/ρ=10/0.6=16.7（秒）。同样：对给定了到达间隔时间Ta时，也可求得Ts以达到满意的服务质量。

整理课件 t=30秒=>μt=3。查曲线得Pw(3)≤0.853.6排队系统建模（1）以排队论方法为基础的仿真模型设计技术主要适用于带时标的随机DEDS系统。 对排队系统来说，它只有两个基本的操作：“入队”和“离队”操作。排队模型的确切形式取决于服务设备的数量和排队线的数量。整理课件3.6排队系统建模（1）以排队论方法为基础的仿真模型设计技86开始对到达的动态实体做相关记录服务设备忙将实体挂在排队线上排队线长度加1设置服务设备为“忙”状态确定（此次）服务时间调度服务完成事件结束

Y N （时间）

入队操作

整理课件开始对到达的动态实体做相关记录服务设备忙将实体挂排队线长度加87设置服务设备为“空”状态排队线“空”按排队规则从队列中选出一个实体记录，让设备为它服务；累计等待时间确定（此次）服务时间；队列统计记录，队长度减1调度服务完成事件结束开始

Y N

离队操作整理课件设置服务设备为“空”状态排队线“空”按排队规则从队列中选出一88(2)Petri网络模型

Petri网模型最早在1962年CarlAdamPetri的博士论文中提出来，主要特性是具有较强的对并行、不确定性、异步和分布的描述能力和分析能力。 Petri网是一个模型化的工具，它是设想来用于模型化某一类问题：即有同时平行事件的离散事件的系统的问题。Petri网模型化了系统，特别是系统的两个方面（事件和条件）及它们之间的关系。整理课件(2)Petri网络模型整理课件89整理课件整理课件90整理课件整理课件91(3)有限状态自动机模型

离散事件系统自动机及形式语言理论最早是由P.J.Ramadge和W.M.Wonbarn等人八十年代中期提出的,现已成为DEDS研究的重要方法之一。 有限状态自动机模型描述方法主要适用于逻辑定性模型和无时标确定性模型的建模。建立有限状态自动机模型的关键是,基于适当的仿真策略选用相应状态集合,建立正确的转移关系函数和输出关系函数。整理课件(3)有限状态自动机模型整理课件924.离散事件仿真策略与结构模型

仿真过程的运行调度控制（特别是在用高级语言编程时），是通过所谓的“仿真策略”来实现的。 例：对一个含有一些出纳员，一些顾客和对应每个出纳员的银行（多）排队线的系统。 设：出纳员数量 5服务速度N(3,1) 顾客 到达 [0.2,0.8] 统计 队列长度（平均，最大，最小，方差） 出纳员利用率（平均，最大，最小，方差） 顾客在银行的时间（平均，最大，最小，方差）

整理课件4.离散事件仿真策略与结构模型 仿真过程的运行调度控制（93可以画出仿真程序的结构框图如下：预定仿真时间TIME=0预定第一个顾客到达时间开始TIME<仿真预定时间有顾客到达选择排队线将顾客插入排队线*调度下一个顾客的到达时间输出统计结果结束在这一段时间内有事务处理完（出纳空）顾客离去选择排队线上的顾客给予服务*调度为该顾客服务的完成时间TIME=TIME+1N

YN 到达事件 Y

N

Y整理课件可以画出仿真程序的结构框图如下：预定仿真时间开始TIME<仿94

这是种“面向时间”的时钟(TIME)处理。通过多次运行程序（试验）统计得到结果。程序每做一次循环，就增加一个时间单位。此时不论系统是否有时间发生，程序总是要查询系统状态，如发现没有时间发生就跳过该事件的处理程序。 这种方法的特点是：能和连续模型（进行时间离散）混合仿真。当事件子程序均能在一个时间单位内处理完成，则TIME的+1操作可以在机器硬件时钟的控制下执行，即仿真程序可以实时的（与机器时钟同步）运行。 缺点是：计算机做了很多不必要的空操作。因为在两个相邻事件时刻之间，系统没有活动需要计算机处理。目前很少使用此方法。 人们在研究了各种（离散）仿真调度方法的基础上，总结出三种通用的仿真策略，即：事件预定，活动扫描和进程互配。整理课件 这是种“面向时间”的时钟(TIME)处理。通过多次运行程954.1面向事件结构模型

面向事件结构模型是按事件独立预定策略组建成的。对上述的银行系统为例，其仿真程序结构框图：

整理课件4.1面向事件结构模型 面向事件结构模型是按事件独立预96TIME<仿真时间开始调度第一次到达事件从事件表中选出最先要执行的事件作为当前事件将时间TIME拨到当前事件的发生时刻按当前事件类型分支选择排队线将顾客插入该排队线调度下一次到达事件的产生时刻顾客离去选排队线上某顾客接受服务或“空闲”出纳员调度本次服务完成（时间）输出统计结果结束

产生第一个顾客到达，填入事件表

N Y到达事件 …… 事务完成整理课件TIME<仿真时间开始调度第一次到达事件从事件表中选出最先要97事件表结构：序号事件发生时间事件类型实体号:i100到达10i+1111接受服务8:k’201离去8k210到达11k+1整理课件事件表结构：序号事件发生时间事件类型实体号:i100到达1098面向事件结构模型

在这里，仿真时钟TIME是根据当前事件的发生时刻进行离散变化的。 “事件预定策略”强调：预定全部事件。事件将按显式调度。“事件功能”由事件程序实现。事件的调度是通过把事件按“事件标志”放在事件表中的方法来达到的。整理课件面向事件结构模型 在这里，仿真时钟TIME是根据当前事件的994.2活动扫描结构模型

当事件的发生不仅与时间有关，而且与其它条件也有关，即：只有在满足某些条件时发生。在这种情况下，由于活动持续时间的不确定性，无法预定活动的开始或终止时间。所以不易采用面向事件的结构模型。而活动扫描结构模型就是针对具有这种特点的系统的。整理课件4.2活动扫描结构模型 当事件的发生不仅与时间有关，而100活动扫描结构模型

活动扫描结构要求对事件隐式调度。在这里，状态的转换被表示成一组称之为“活动”的函数。 每次转换，由一个活动条件和一个动作组成。在每个（由预定事件生成时刻确定的）时间上，按某种（总体状态的）顺序扫描这些条件，如果出现一个条件是真，则立即执行与它联系的“动作”段；继续扫描，测试和执行，直到满足条件的活动都进行完。这是再按下一预定事件生成时刻向前推进模型的时钟。整理课件活动扫描结构模型 活动扫描结构要求对事件隐式调度。在这里，101活动扫描结构模型

按某种（总体状态）顺序扫描这些任务（包括检测小于当前时间应发生，但因条件未满足而延时发生的“以前”事件）。 在使用活动扫描策略时，需要借助事件预定策略进行时间（钟）管理。 事件预定策略不但要按预定事件的生成时刻