【其中考试】 河南省安阳市安阳示范区飞翔中学初三（上）期中考试数学试卷

试卷第=page3434页，总=sectionpages3434页试卷第=page3333页，总=sectionpages3434页2021-2022学年河南省安阳市安阳示范区飞翔中学初三（上）期中考试数学试卷一、选择题

1.用配方法解方程x2-6xA.x-32=10 B.x

2.下列关于二次函数y=-xA.该函数图象的开口向上B.该函数图象的顶点坐标为2,3C.当x<2时，y随xD.该函数的最大值为7

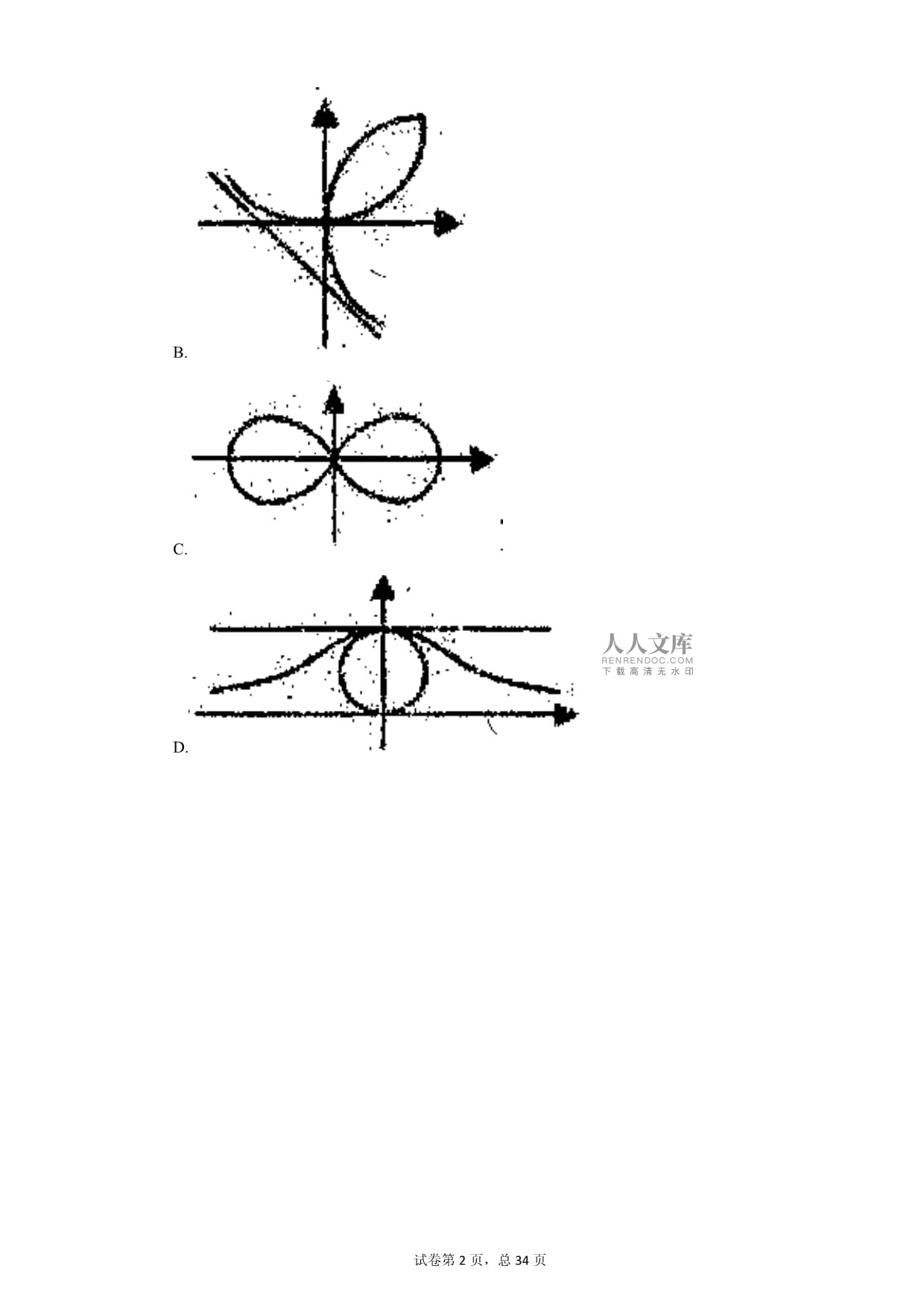
3.数学世界奇妙无穷，其中曲线是微分几何的研究对象之一，下列数学曲线既是轴对称图形，又是中心对称图形的是（

）A.B.C.D.

4.如图，AB为⊙O的直径，弦CD⊥AB于点E

，连接AC，OC，OD，若∠COD=80∘，则A.20∘ B.40∘ C.60

5.若关于x的一元二次方程kx2-6x+9=0A.k<1 B.k<1且k≠0 C.

6.如图，四边形ABCD内接于圆O，∠DCE=65∘，则∠A的度数为（A.112∘ B.68∘ C.65

7.在“石头、剪子、布”的游戏中，当你出“剪刀”时，对手与你打平的概率为（

）A.12 B.13 C.2

8.同一坐标系中，一次函数y=ax+b与二次函数yA.B.C.D.

9.如图，在△OAB中，顶点O(0,0)，A(-3,4)，B(3,4)，将△OAB与正方形ABCD组成的图形绕点O顺时针旋转，每次旋转90∘，则第A.(10,3) B.(-3,10) C.(10,-3) D.(3,-10)

10.如图1，矩形ABCD中，点E为BC的中点，点P沿BC从点B运动到点C，设B，P两点间的距离为x，PA-PE=y图2是点P运动时y随x变化的关系图象，则BC的长为（

）A.4 B.5 C.6 D.7二、填空题

一元二次方程x2-x=0

如图，△ABO中，AB⊥OB, OB=23, AB=2，把△ABO绕点O顺时针旋转150∘后得到

△A1

如图，抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)和B，与y轴的正半轴交于点C，下列结论：

如图，在平面直角坐标系中，△OAB的顶点O是坐标原点，AO=AB=5, OB=6.将△AOB绕点B按顺时针方向旋转一定角度后得△A'O'B,点A的对应点

如图，将半径为2，圆心角为120∘的扇形OAB绕点A逆时针旋转60∘，点O，B的对应点分别为O'

，B'，连接BB'三、解答题

在如图所示的网格中按要求画出图形：

(1)画出△ABC以点O为旋转中心顺时针旋转90∘后的(2)画出△ABC关于点O的中心对称图形△

某中学在艺术节期间向全校学生征集书画作品，美术王老师从全校随机抽取了四个班级记作A，B，C，D，对征集到的作品的数量进行了分析统计，制作了如下两幅不完整的统计图．

(1)王老师抽查的四个班级共征集到________件作品；(2)请把图2的条形统计图补充完整；(3)若全校参展作品中有三名同学获得一等奖，其中有一名男生、二名女生．现在要在其中抽两名同学去参加学校总结表彰座谈会，请用画树状图或列表的方法求恰好抽中一名男生一名女生的概率．

某童装专卖店在销售中发现，一款童装每件进价为80元，销售价为120元时，每天可售出20件，为了迎接“五一”国际劳动节，商店决定采取适当的降价措施，以扩大销售量，尽快减少库存，增加利润．经市场调查发现，如果每件童装降价1元，那么平均可多售出2件．(1)设每件童装降价x元时，每天可销售________件，每件盈利________元；（用x的代数式表示）(2)为了扩大销售量，尽快减少库存，每件童装降价多少元时，平均每天盈利1200元；(3)平均每天盈利1300元，可能吗？请说明理由．D

如图，已知AB是⊙O的直径，C是⊙O上的点，点D在AB的延长线上，∠(1)求证：CD是⊙O(2)∠D=30∘，BD=4，求AC的长.

如图，在矩形ABCD中，AB=12cm,BC=6cm.点P沿AB边从点A开始向点B以2cm/s的速度移动，点Q沿DA边从点D开始向点A以1cm/s的速度移动．如果P、Q同时出发，用t（s

如图，抛物线y=x2-2x+c与x轴正半轴，y轴负半轴分别相交于点A，B(1)求抛物线的解析式及点G的坐标：(2)点M，N为抛物线上两点（点M在点N的左侧），且到对称轴的距离分别为3个单位长度和4个单位长度，点Q为抛物线上点M，N之间（不含点M，N）的一个动点，求点Q的纵坐标yQ

我们学习过利用尺规作图平分一个任意角，而“利用尺规作图三等分一个任意角”曾是数学史上一大难题，之后被数学家证明是不可能完成的．人们根据实际需要，发明了一种简易操作工具一一三分角器．图1是它的示意图，其中AB与半圆O的直径BC在同一直线上，且AB的长度与半圆的半径相等；DB与AC垂直于点B，DB足够长．

使用方法如图2所示，若要把∠MEN三等分，只需适当放置三分角器，使DB经过∠MEN的顶点E，点A落在边EM上，半圆O与另一边EN恰好相切，切点为F，则EB，EO就把∠MEN三等分了．

为了说明这一方法的正确性，需要对其进行证明．如下给出了不完整的“已知”和“求证”，请补充完整，并写出“证明”过程．

已知：如图2，点A，B，O，C在同一直线上，BB⊥AC垂足为点B，________.

阅读与理解：

图1是边长分别为a和ba>b的两个等边三角形纸片ABC和C'DE叠放在一起（C与C'重合）的图形．

(1)操作：固定△ABC将△C'DE绕点C按顺时针方向旋转30∘，连接AD，BE，如图2；在图2(2)操作：若将图1中的△C'DE绕点C按顺时针方向任意旋转一个角度α(0∘≤a≤360∘），连接AD，BE，如图3；在图3中，线段BE与AD之间具有怎样的大小关系？证明你的结论；

猜想与发现：

参考答案与试题解析2021-2022学年河南省安阳市安阳示范区飞翔中学初三（上）期中考试数学试卷一、选择题1.【答案】A【考点】解一元二次方程-配方法【解析】此题暂无解析【解答】解：∵x2-6x-1=0，

∴x2-6x=12.【答案】D【考点】二次函数的性质二次函数图象上点的坐标特征【解析】根据题目中的函数解析式和二次函数的性质，可以判断各个选项中的说法是否正确．【解答】解：二次函数y=-x2+4x+3=-x2-4x+3=-x-22+7，

∵a=-1<0，

∴该函数的图象开口向下，

对称轴是直线x=2，它的顶点坐标为2,7，最大值为73.【答案】C【考点】轴对称图形中心对称图形轴对称与中心对称图形的识别【解析】此题暂无解析【解答】解：A．是轴对称图形，不是中心对称图形，故此选项不合题意；

B．是轴对称图形，不是中心对称图形，故此选项不合题意；

C．既是中心对称图形，也是轴对称图形，符合题意；

D．是轴对称图形，不是中心对称图形，故此选项不合题意．

故选C．4.【答案】A【考点】垂径定理圆周角定理【解析】此题暂无解析【解答】解：∵AB是直径，AB⊥CD，∴DB=BC，

∴∠DOB=∠BOC=5.【答案】B【考点】根的判别式【解析】此题暂无解析【解答】解：根据题意得k≠0且Δ=-62-4×k×9>06.【答案】C【考点】圆内接四边形的性质【解析】此题暂无解析【解答】解：∵四边形ABCD内接于⊙O，∴∠BAD+∠BCD=180∘，

∵∠BCD7.【答案】B【考点】概率公式列表法与树状图法【解析】此题暂无解析【解答】解：画树状图为：

共有3种可能的结果数，其中对手与你打平的结果数为1，所以对手与你打平的概率=13.

故选B8.【答案】B【考点】一次函数的图象二次函数的图象【解析】此题暂无解析【解答】解：A、由一次函数y=ax+b的图象可得a<0，由二次函数y=ax2+b的图象可得a>0，故A不可能；

B、由一次函数y=ax+b的图象可得a>0,b>0，由二次函数y=ax2+b的图象可得a>0，b>0，故B有可能；

C9.【答案】D【考点】坐标与图形变化-旋转正方形的性质【解析】此题暂无解析【解答】解：∵A(-3,4)，B(3,4)，

∴AB=3+3=6，

∵四边形ABCD为正方形，

∴AD=AB=6，

∴D(-3,10)，

∵70=4×17+2，

∴每4次一个循环，第70次旋转结束时，

相当于△OAB与正方形ABCD组成的图形绕点O顺时针旋转2次，

每次旋转90∘10.【答案】C【考点】动点问题勾股定理【解析】此题暂无解析【解答】解：由函数图象知：当x=0，即P在B点时，

BA-BE=1.

利用两点之间线段最短，得到PA-PE≤AE,

∴y的最大值为AE，

∴AE=5.

在Rt△ABE中，由勾股定理得：

BA2+BE2=AE2=25,

设BE的长度为t，

则BA=t+1,

∴t+12+二、填空题【答案】x1=0【考点】一元二次方程的解【解析】本题考查解一元二次方程.【解答】解：x2-x=0，

x(x-1)=0，

x=0或x-1=0，

【答案】(-3,-【考点】勾股定理坐标与图形变化-旋转【解析】此题暂无解析【解答】解．如图，过点B1作B1H⊥x轴于H．

∵∠BOB1=150∘，

∴∠HOB1=180【答案】①②【考点】二次函数的图象二次函数的性质【解析】此题暂无解析【解答】解：∵抛物线的开口向下，∴a<0，

∵抛物线的对称轴为直线x=-1，∴-b2a=-1，

∴b=2a<0.

当x=0时，y=c>0，

∴abc>0

∴①正确，

根据图象可得，当x=-2时，

y【答案】O【考点】勾股定理旋转的性质【解析】此题暂无解析【解答】解：∵AO=AB，

AC⊥OB，∴OC=BC=3，

在Rt△ACO中，

∠ACO=90∘，

∴AC=AO2-OC2=52-32=4，

∴点A的坐标为3,4，

由旋转的性质可知，△AOB≅ΔA'O'B，

∴A'B=AB【答案】2【考点】扇形面积的计算求阴影部分的面积旋转的性质【解析】此题暂无解析【解答】解：连接OO',BO'，

∵将半径为2，圆心角为120∘的扇形OAB绕点A逆时针旋转60∘，

∴∠OAO'=60∘，

∴△OAO'是等边三角形，

∴∠AOO'=60∘，

∵∠AOB=120∘三、解答题【答案】解：（1）如图，△A（2）如图，△A2B【考点】作图-旋转变换中心对称【解析】此题暂无解析【解答】解：（1）如图，△A（2）如图，△A2B【答案】12(2)12-2-5-2=3（件），

故B班征集到3件作品．

条形统计图补充完整如图：

(3)画树状图如下：

共有6种等可能的情况，其中恰好抽中一名男生一名女生的有4种情况，

故恰好抽中一名男生一名女生的概率是P=4【考点】条形统计图扇形统计图用样本估计总体列表法与树状图法【解析】(1)用C班的人数除以该班的作品数得到调查的总作品数；(2)计算出B班的作品数，再补全条形统计图；(3)画树状图展示所有6种等可能的结果数，找出恰好抽中一名男生一名女生的结果数，然后根据概率公式计算．【解答】解：(1)5÷150360=12（件），

故王老师抽查的四个班级共征集到12件作品．

(2)12-2-5-2=3（件），

故B班征集到3件作品．

条形统计图补充完整如图：

(3)画树状图如下：

共有6种等可能的情况，其中恰好抽中一名男生一名女生的有4种情况，

故恰好抽中一名男生一名女生的概率是P=4【答案】20+2x,40-（2）设每件童装降价y元，则每件盈利40-y元，每天的销售量为20+2y件，

依题意得：40-y20+2y=1200，

整理得：y2-30x+200=0，

解得：y1=10,y（3）不可能，理由如下：

设每件童装降价m元，则每件盈利40-m元，每天的销售量为20+2m件，依题意得：40-m20+2m=1300，

整理得：m2-【考点】列代数式一元一次方程的应用——打折销售问题一元二次方程的应用——利润问题【解析】此题暂无解析【解答】解：（1）若每件童装降价x元，则每天可销售20+2x件，每件盈利(120-x-80)=(40-x)元．

（2）设每件童装降价y元，则每件盈利40-y元，每天的销售量为20+2y件，

依题意得：40-y20+2y=1200，

整理得：y2-30x+200=0，

解得：y1=10,y（3）不可能，理由如下：

设每件童装降价m元，则每件盈利40-m元，每天的销售量为20+2m件，依题意得：40-m20+2m=1300，

整理得：m2-【答案】(1)证明：连接OC，

∵OA=OC，

∴∠BAC=∠OCA.

∵∠BCD=∠BAC，

∴∠BCD=∠OCA.

∵AB是直径，

∴∠ACB=90∘，

∴(2)解：设⊙O的半径为r，

∴AB=2r，

∵∠D=30∘，∠OCD=90∘，

∴OD=2r，∠COB【考点】圆周角定理切线的判定勾股定理的应用【解析】(1)连接OC，易证∠BCD=∠OCA，由于AB是直径，所以∠ACB=90∘，所以(2)设⊙O的半径为r，AB=2r，由于∠D=30∘，∠OCD=90∘，所以可求出r=2【解答】(1)证明：连接OC，

∵OA=OC，

∴∠BAC=∠OCA.

∵∠BCD=∠BAC，

∴∠BCD=∠OCA.

∵AB是直径，

∴∠ACB=90∘，

∴(2)解：设⊙O的半径为r，

∴AB=2r，

∵∠D=30∘，∠OCD=90∘，

∴OD=2r，∠COB【答案】解：当运动时间为ts

时，AP=2tcm

，AQ=6-tcm，依题意得:12×2t6-t=8，

整理得t2-6t【考点】三角形的面积动点问题一元二次方程的应用——其他问题【解析】此题暂无解析【解答】解：当运动时间为ts

时，AP=2tcm

，AQ=6-tcm，依题意得:12×2t6-t=8，

整理得t2-6【答案】解：（1）取x=0，则y=c，∴B（0，c），∴A-c,0,

把点A代入抛物线的解析式，

得：0=-c2-2×-c+c（2）∵点M到对称轴的距离为3个单位，

∴xM=1-3=-2或xM=1+3=4,

∴yM=5,

∴M-2,5或M4,5,

∵点N到对称轴的距离为4个单位，

∴xN=1-4=-3或xN=1+4=5,

∴yN=12,

∴N(-3,12)或N5,12,

又∵M在N的左侧，

∴M，N的坐标为-2,5,5,12或4,5,5,12,

若【考点】待定系数法求二次函数解析式二次函数图象上点的坐标特征二次函数的性质【解析】此题暂无解析【解答】解：（1）取x=0，则y=c，∴B（0，c），∴A-c,0,

把点A代入抛物线的解析式，

得：0=-c2-2×-c+c,（2）∵点M到对称轴的距离为3个单位，

∴xM=1-3=-2或xM=1+3=4,

∴yM=5,

∴M-2,5或M4,5,

∵点N到对称轴的距离为4个单位，

∴xN=1-4=-3或xN=1+4=5,

∴yN=12,

∴N(-3,12)或N5,12,

又∵M在N的左侧，

∴M，N的坐标为-2,5,5,12或4,5,5,12,

若【答案】解：已知：如图2，点A，B，O，C在同一直线上，EB⊥AC，垂足为点B，AB=OB，EN切半圆O于F．

求证：EB，EO就把∠MEN三等分，

证明：∵EB⊥AC，

∴∠ABE=∠