河南省漯河召陵区七校联考2023学年九年级数学第一学期期末监测模拟试题含解析

1、2023学年九上数学期末模拟试卷考生请注意：1答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。2第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。3考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。一、选择题（每题4分，共48分）1若，则的值是（ ）ABCD02如图1，点P从ABC的顶点A出发，沿ABC匀速运动，到点C停止运动点P运动时，线段AP的长度y与运动时间x的函数关系如图2所示，其中D为曲线部分的最低点，则ABC的面积是（）A10B12C20D243如图所示，某宾馆大厅要铺圆

2、环形的地毯，工人师傅只测量了与小圆相切的大圆的弦AB的长，就计算出了圆环的面积，若测量得AB的长为20米，则圆环的面积为( )A10平方米B10平方米C100平方米D100平方米4如图，在平面直角坐标系中，M、N、C三点的坐标分别为（，1），（3，1），（3，0），点A为线段MN上的一个动点，连接AC，过点A作ABAC交y轴于点B，当点A从M运动到N时，点B随之运动，设点B的坐标为（0，b），则b的取值范围是（）Ab1Bb1CbDb15如图所示，在中，则长为（ ）ABCD6截止到2018年底,过去五年我国农村贫困人口脱贫人数约为7 000万,脱贫攻坚取得阶段性胜利,这里“7 000万”用科学记

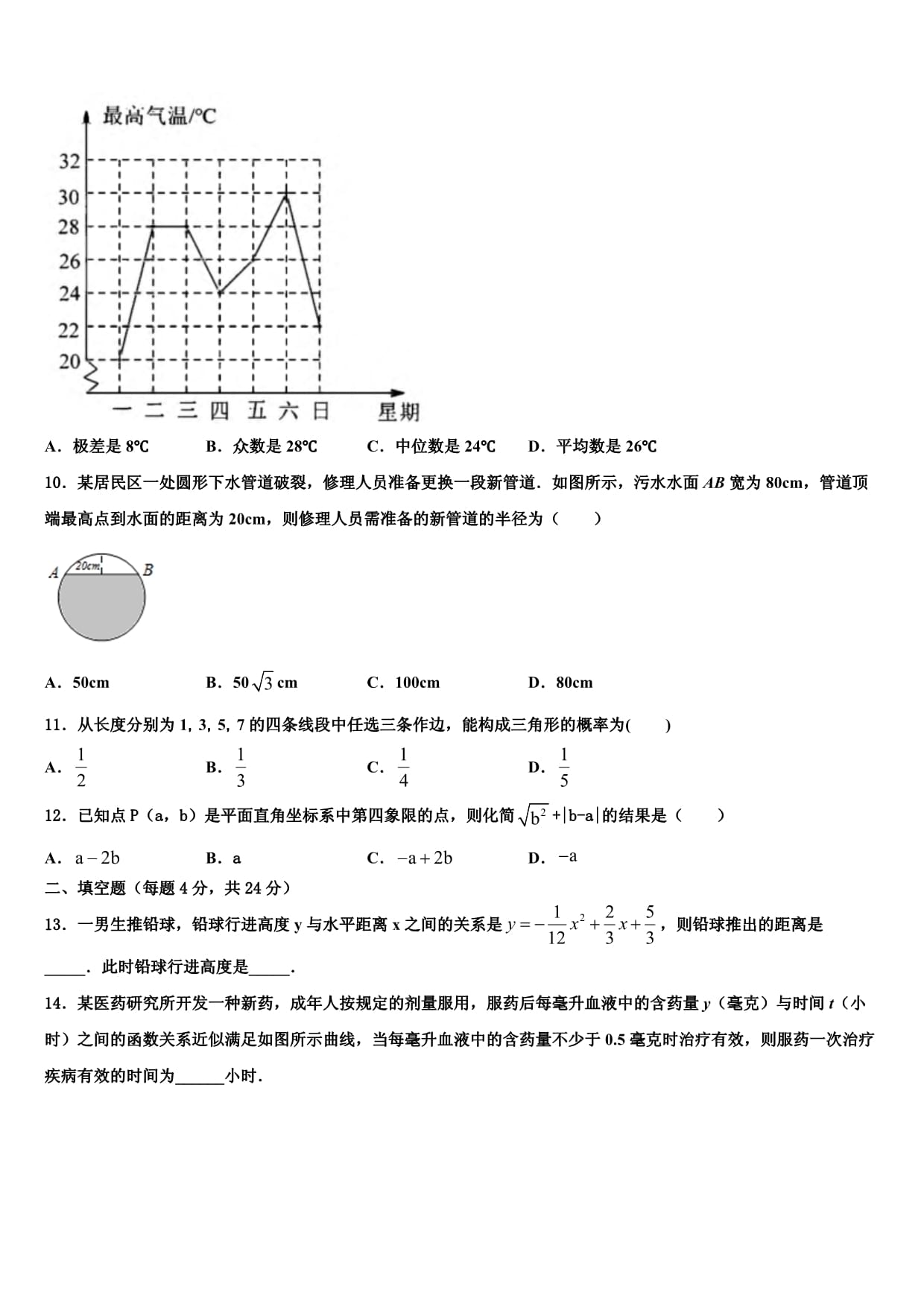
3、数法表示为()A7103B7108C7107D0.71087给出下列函数，其中y随x的增大而减小的函数是（ ）y2x；y2x+1；y（x0）；yx2（x1）ABCD8如图，已知在ABC中，P为AB上一点，连接CP，以下条件中不能判定ACPABC的是（）ABCD9如图是成都市某周内日最高气温的折线统计图，关于这7天的日最高气温的说法正确的是（ ）A极差是8B众数是28C中位数是24D平均数是2610某居民区一处圆形下水管道破裂，修理人员准备更换一段新管道如图所示，污水水面AB宽为80cm，管道顶端最高点到水面的距离为20cm，则修理人员需准备的新管道的半径为（）A50cmB50cmC100cmD

4、80cm11从长度分别为1，3，5，7的四条线段中任选三条作边，能构成三角形的概率为( )ABCD12已知点P（a，b）是平面直角坐标系中第四象限的点，则化简+|b-a|的结果是（）ABaCD二、填空题（每题4分，共24分）13一男生推铅球，铅球行进高度y与水平距离x之间的关系是，则铅球推出的距离是_此时铅球行进高度是_14某医药研究所开发一种新药，成年人按规定的剂量服用，服药后每毫升血液中的含药量y（毫克）与时间t（小时）之间的函数关系近似满足如图所示曲线，当每毫升血液中的含药量不少于0.5毫克时治疗有效，则服药一次治疗疾病有效的时间为_小时15若P的半径为5，圆心P的坐标为（3，4），则平

5、面直角坐标系的原点O与P的位置关系是_16九年级学生在毕业前夕，某班每名同学都为其他同学写一段毕业感言，全班共写了2256段毕业感言，如果该班有x名同学，根据题意列出方程为_17如图，在菱形ABCD中，E，F分别是AD，BD的中点，若EF=2，则菱形ABCD的周长是_18如图，在中，用含和的代数式表示的值为：_三、解答题（共78分）19（8分）富平因取“富庶太平”之意而得名，是华夏文明重要发祥地之一.某班举行关于“美丽的富平”的演讲活动.小明和小丽都想第一个演讲，于是他们通过做游戏来决定谁第一个来演.讲游戏规则是：在一个不透明的袋子中有一个黑球a和两个白球b、c，(除颜色外其它均相同)，小丽从

6、袋子中摸出一个球，放回后搅匀，小明再从袋子中摸出一个球，若两次摸到的球颜色相同，则小丽获胜，否则小明获胜，请你用树状图或列表的方法分别求出小丽与小明获胜的概率，并说明这个游戏规则对双方公平吗？20（8分）画出如图所示的几何体的主视图、左视图和俯视图21（8分）如图，抛物线与轴相交于两点，点在点的右侧，与轴相交于点.求点的坐标；在抛物线的对称轴上有一点，使的值最小，求点的坐标；点为轴上一动点，在抛物线上是否存在一点，使以四点构成的四边形为平行四边形?若存在，求点的坐标；若不存在，请说明理由.22（10分）在RtABC中，C=90，AC=，BC=.解这个直角三角形.23（10分）如图，在中，点在的

7、内部，经过，两点，交于点，连接并延长交于点，以，为邻边作（1）判断与的位置关系，并说明理由（2）若点是的中点，的半径为2，求的长24（10分）学生会组织周末爱心义卖活动，义卖所得利润将全部捐献给希望工程，活动选在一块长米、宽米的矩形空地上.如图，空地被划分出个矩形区域，分别摆放不同类别的商品，区域之间用宽度相等的小路隔开，已知每个区域的面积均为平方米，小路的宽应为多少米?25（12分）如图，在平面直角坐标系中，已知矩形的顶点，过点的双曲线与矩形的边交于点(1)求双曲线的解析式以及点的坐标；(2)若点是抛物线的顶点；当双曲线过点时，求顶点的坐标；直接写出当抛物线过点时，该抛物线与矩形公共点的个数

8、以及此时的值26用适当的方法解下列方程：（1） （2）参考答案一、选择题（每题4分，共48分）1、D【分析】设，则a=2k，b=3k，代入式子化简即可【详解】解：设，a=2k，b=3k，=0，故选D.【点睛】本题考查比例线段，解题的关键是学会利用参数解决问题，属于中考常考题型2、B【解析】过点A作AMBC于点M，由题意可知当点P运动到点M时，AP最小，此时长为4，观察图象可知AB=AC=5，BM=3，BC=2BM=6，SABC=12，故选B.【点睛】本题考查了动点问题的函数图象，根据已知和图象能确定出AB、AC的长，以及点P运动到与BC垂直时最短是解题的关键.3、D【解析】过O作OCAB于C，

9、连OA，根据垂径定理得到AC=BC=10，再根据切线的性质得到AB为小圆的切线，于是有圆环的面积=OA2-OC2=（OA2-OC2）=AC2，即可圆环的面积【详解】过O作OCAB于C，连OA，如图，AC=BC，而AB=20，AC=10，AB与小圆相切，OC为小圆的半径，圆环的面积=OA2-OC2=（OA2-OC2）=AC2=100（平方米）故选D【点睛】本题考查了垂径定理：垂直于弦的直径平分弦，并且平分弦所对的弧也考查了切线的性质定理以及勾股定理4、B【分析】延长NM交y轴于P点，则MNy轴连接CN证明PABNCA，得出，设PAx，则NAPNPA3x，设PBy，代入整理得到y3xx2（x）2+

10、，根据二次函数的性质以及x3，求出y的最大与最小值，进而求出b的取值范围【详解】解：如图，延长NM交y轴于P点，则MNy轴连接CN在PAB与NCA中， ，PABNCA，设PAx，则NAPNPA3x，设PBy，y3xx2（x）2+，10，x3，x时，y有最大值，此时b1，x3时，y有最小值0，此时b1，b的取值范围是b1故选：B【点睛】本题考查了相似三角形的判定与性质，二次函数的性质，得出y与x之间的函数解析式是解题的关键5、B【分析】先根据同角的三角函数值的关系得出，解出AC=5，再根据勾股定理得出AB的值.【详解】在中，即.又AC=5=3.故选B.【点睛】本题考查了三角函数的值，熟练掌握同角

11、的三角函数的关系是解题的关键.6、C【分析】科学记数法的表示形式为的形式，其中，为整数确定的值时，要看把原数变成时，小数点移动了多少位，的绝对值与小数点移动的位数相同【详解】将数据7 000万用科学记数法表示为故选：C【点睛】本题考查科学记数法的表示方法科学记数法的表示形式为的形式，其中，为整数，表示时关键要正确确定的值以及的值7、D【解析】分别根据一次函数、二次函数及反比例函数的增减性进行解答即可【详解】解：y=2x中k=20，y随x的增大而增大，故本小题错误；y=-2x+1中k=-20，y随x的增大而减小，故本小题正确；y=（x0）中k=20，x0时，y随x的增大而减小，故本小题正确；y=

12、x2（x1）中x1，当0 x1时，y随x的增大而增大，故本小题错误故选D【点睛】本题考查的是反比例函数的性质，熟知一次函数、二次函数及反比例函数的增减性是解答此题的关键8、C【分析】A、加一公共角，根据两角对应相等的两个三角形相似可以得结论；B、加一公共角，根据两角对应相等的两个三角形相似可以得结论；C、其夹角不相等，所以不能判定相似；D、其夹角是公共角，根据两边的比相等，且夹角相等，两三角形相似【详解】A、A=A，ACP=B，ACPABC，所以此选项的条件可以判定ACPABC；B、A=A，APC=ACB，ACPABC，所以此选项的条件可以判定ACPABC；C、，当ACP=B时，ACPABC，

13、所以此选项的条件不能判定ACPABC；D、，又A=A，ACPABC，所以此选项的条件可以判定ACPABC，本题选择不能判定ACPABC的条件，故选C【点睛】本题考查了相似三角形的判定，熟练掌握相似三角形的判定方法是关键9、B【解析】分析：根据折线统计图中的数据可以判断各个选项中的数据是否正确，从而可以解答本题详解：由图可得，极差是：30-20=10，故选项A错误，众数是28，故选项B正确，这组数按照从小到大排列是：20、22、24、26、28、28、30，故中位数是26，故选项C错误，平均数是：，故选项D错误，故选B点睛：本题考查折线统计图、极差、众数、中位数、平均数，解答本题的关键是明确题意

14、，能够判断各个选项中结论是否正确10、A【分析】连接OA作弦心距，就可以构造成直角三角形设出半径弦心距也可以得到，利用勾股定理就可以求出了【详解】解：如图，过点O作于点C，边接AO，在中，解，得AO=50故选：A【点睛】本题考查的是垂径定理的应用，根据题意作出辅助线，构造出直角三角形是解答此题的关键11、C【分析】从四条线段中任意选取三条，找出所有的可能，以及能构成三角形的情况数，即可求出所求的概率【详解】解：从四条线段中任意选取三条，所有的可能有：1，3，5；1，3，7；1，5，7；3，5，7共4种，其中构成三角形的有3，5，7共1种，能构成三角形的概率为：，故选C点睛：此题考查了列表法与树

15、状图法，以及三角形的三边关系，用到的知识点为：概率=所求情况数与总情况数之比12、A【解析】根据第四象限的点的横坐标是正数，纵坐标是负数，求解即可【详解】点P(a,b)是平面直角坐标系中第四象限的点，a0，b0，ba0，+|b-a|=b(ba)=bb+a=2b+a=a2b，故选A.【点睛】本题考查点的坐标， 二次根式的性质与化简，解题的关键是根据象限特征判断正负.二、填空题（每题4分，共24分）13、1 2 【分析】铅球落地时，高度，把实际问题理解为当时，求x的值即可【详解】铅球推出的距离就是当高度时x的值当时，解得：（不合题意，舍去）则铅球推出的距离是1此时铅球行进高度是2故答案为：1；2【

16、点睛】本题考查了二次函数的应用，理解铅球推出的距离就是当高度时x的值是解题关键14、7.1【分析】将点（1，4）分别代入y=kt， 中，求k、m，确定函数关系式，再把y=0.5代入两个函数式中求t，把所求两个时间t作差即可【详解】解：把点（1，4）分别代入y=kt，中，得k=4，m=4，y=4t，把y=0.5代入y=4t中，得t1=，把y=0.5代入中，得t2=，治疗疾病有效的时间为：t2-t1=故答案为：7.1【点睛】本题考查了本题主要考查函数模型的选择与应用、反比例函数、一次函数的实际应用关键是用待定系数法求函数关系式，理解题意，根据已知函数值求自变量的差15、点O在P上【分析】由勾股定理

17、等性质算出点与圆心的距离d，则dr时，点在圆外；当d=r时，点在圆上；当dr时，点在圆内【详解】解：由勾股定理，得OP5，dr5，故点O在P上故答案为点O在P上.【点睛】此题考查点与圆的位置关系的判断解题关键在于要记住若半径为r，点到圆心的距离为d，则有：当dr时，点在圆外；当d=r时，点在圆上，当dr时，点在圆内16、（x1）x2256【分析】根据题意得：每人要写（x-1）条毕业感言，有x个人，然后根据题意可列出方程【详解】根据题意得：每人要写(x1)条毕业感言，有x个人，全班共写：(x1)x=2256，故答案为：(x1)x=2256.【点睛】此题考查一元二次方程，解题关键在于结合实际列一元

18、二次方程即可.17、1【解析】试题分析：先利用三角形中位线性质得到AB=4，然后根据菱形的性质计算菱形ABCD的周长E，F分别是AD，BD的中点， EF为ABD的中位线， AB=2EF=4，四边形ABCD为菱形， AB=BC=CD=DA=4， 菱形ABCD的周长=44=1考点：（1）菱形的性质；（2）三角形中位线定理18、【分析】分别在RtABC和RtADC中用AC和的三角函数表示出AB和AD，进一步即可求出结果【详解】解：在RtABC中，在RtADC中，故答案为：【点睛】本题考查了三角函数的知识，属于常考题型，熟练掌握正弦的定义是解题的关键三、解答题（共78分）19、小丽为，小军为，这个游戏

19、不公平，见解析【分析】画出树状图，得出总情况数及两次模到的球颜色相同和不同的情况数，即可得小丽与小明获胜的概率，根据概率即可得游戏是否公平.【详解】根据题意两图如下：共有种等情况数，其中两次模到的球颜色相同的情况数有种，不同的有种，小丽获胜的概率是小军获胜的概率是，所以这个游戏不公平.【点睛】本题考查游戏公平性的判断，判断游戏的公平性要计算每个参与者获胜的概率，概率相等则游戏公平，否则游戏不公平，用到的知识点为：概率=所求情况数与总情况数之比.20、见解析【分析】分别从正面、左面、上面看得到的图形即可.看到的棱用实线表示,实际存在但是被挡住看不见的棱用虚线表示.【详解】【点睛】本题考查了三视图

20、的作图.21、（1），；（2）；（3）点的坐标为，或.【分析】（1）把y=0代入函数解析式，解方程可求得A、B两点的坐标；把x=0代入函数解析式可求得C点的坐标.（2）连接BC，交对称轴于P，P即为使PB+PC的值最小，设直线BC的解析式，把B、C的坐标代入即可求得系数，进而求得解析式，令x=2时，即可求得P的坐标；（3）分两种情况：当存在的点N在x轴的上方时，根据对称性可得点N的坐标为（4，）；当存在的点N在x轴下方时，作辅助线，构建三角形全等，证明得，即N点的纵坐标为-，列方程可得N的坐标【详解】（1）当时，当时，化简，得.解得.连接，交对称轴于点，连接.点和点关于抛物线的对称轴对称，.要

21、使的值最小，则应使的值最小，所以与对称轴的交点使得的值最小.设的解析式为.将代入，可得，解得，抛物线的对称轴为直线当时，当在轴上方，此时，且.则四边形是平行四边形.当在轴下方;作，交于点.如果四边形是平行四边形.又，.当时，综上所述，点的坐标为，或.【点睛】本题考查了待定系数法求二次函数解析式轴对称的性质、平行四边形的判定、三角形全等的性质和判定等知识，难度适中，第2问解题的关键是熟练掌握平行四边形的判定，采用分类讨论的思想和数形结合的思想解决问题22、，.【分析】根据题意和题目中的数据，利用勾股定理，可以求得AB的长，根据锐角三角函数可以求得A的度数，进而求得B的度数，本题得以解决【详解】，.，.答：，.【点睛】本题考查解直角三角形，解答本题的关键是明确题意，利用勾股定理和数形结合的思想解答23、（1）是的切线；理由见解析；（2）的长【分析】（1）连接，求得，根据圆周角定理得到，根据平行四边形的性质得到，得到，推出，于是得到结论；（2）连接，由点是的中点，得到，求得，根据弧长公式即可得到结论【详解】（1）是的切线；理由：连接，四边形是平行四边形，是的切线；（2）连接，点是的中点，的长【点睛】本题考查了直线与圆的位置关系，圆周角定理，平行四边形的性质，正确的识别图形是解题的关键24、小路的宽应为米.【分析】设每条道路的宽为米，则活动区域