人教版辽宁省北票市高中数学 第三章 不等式 3.5.2 简单的线性规划课件1 新人教B必修5

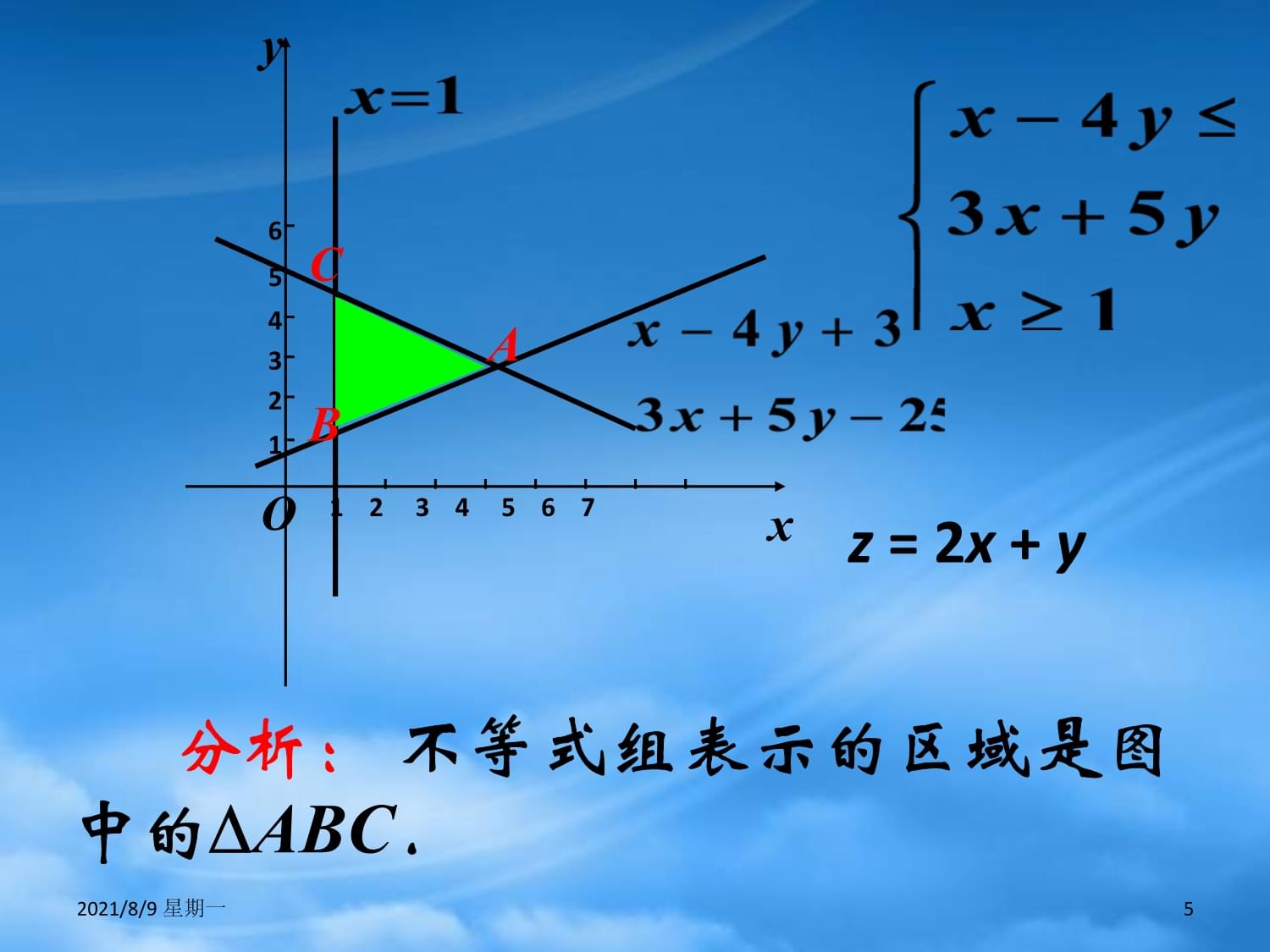
1、2021/8/9 星期一13.5.2简单线性规划2021/8/9 星期一21：画出不等式（组）表示的平面区域： y2x+1 4x-3y9 x+2y4说明：直线定界、特殊点定域划分区域时，找好特殊点，注意不等号。y=2x+1x+2y=4o-1yx112233-2xo123-1-2-3y4x-3y=92021/8/9 星期一33x+5y25x-4y-3x1在该平面区域上 问题 1：有无最大(小)值？问题：有无最大(小)值？xyox-4y=-33x+5y=25x=1问题：2+有无最大(小)值？CAB2021/8/9 星期一4引例 设z = 2x + y，式中变量x、y满足下列条件 求z的最大值和最小

2、值2021/8/9 星期一5xyO1 2 3 4 5 6 7654321ABC 分析：不等式组表示的区域是图中的ABCz = 2x + y2021/8/9 星期一6xyO1 2 3 4 5 6 7654321ABCl2l1求最值的方法1. 截距法 在经过不等式组表示的公共区域内的点且平行于l0的直线中，以经过点A(5，2)的直线 l2 所对应的截距最大故 zmax= 2 5 + 2 = 12，以经过点B(1，1)的直线l1所对应的z最小故 zmin = 2 1 + 1= 32021/8/9 星期一7xyO1 2 3 4 5 6 7654321ABC思考: 2x + y -z= 0(z R)可看

3、作什么? 一组平行直线,都与直线l0：2x + y = 0平行.求最值的方法2. 距离法 2021/8/9 星期一8xyO1 2 3 4 5 6 7654321ABC 作一组与直线l0平行的直线(或平行移动直线l0)l：2x + y = z，z R 求最值的方法2. 距离法 2021/8/9 星期一9xyO1 2 3 4 5 6 7654321ABC 在经过不等式组所表示的公共区域内的点且平行于l的直线中，以经过点A(5，2)的直线l2所对应的d最大，l2求最值的方法2. 距离法 2021/8/9 星期一10 以经过点B(1，1)的直线l1所对应的d最小所以：zmax = 2 5 + 2 =

4、12，zmin = 2 1 + 1= 3xyO1 2 3 4 5 6 7654321ABCl2l1求最值的方法2. 距离法 2021/8/9 星期一11 在上述问题中，不等式组是一组对变量x、y的约束条件，由于这组约束条件都是关于x、y的一次不等式，所以又可称其为线性约束条件z = 2x + y是欲达到最大值或最小值所涉及的变量x、y的解析式，我们把它称为目标函数由于z = 2x + y又是关于x、y的一次解析式，所以又可叫做线性目标函数线性规划的有关概念： 2021/8/9 星期一12线性规划的概念：问题：设z=2x+y，式中变量满足下列条件： 求z的最大值与最小值。 目标函数（线性目标函数

5、）线性约束条件2021/8/9 星期一13 注意：线性约束条件除了用一次不等式表示外，也可用一次方程表示 一般地，求线性目标函数在线性约束条件下的最大值或最小值的问题，统称为线性规划问题例如： 我们刚才研究的就是求线性目标函数z = 2x + y在线性约束条件下的最大值和最小值的问题，即为线性规划问题线性规划的有关概念： 2021/8/9 星期一14 满足线性约束条件的解(x，y)叫做可行解，由所有可行解组成的集合叫做可行域在上述问题中，可行域就是阴影部分表示的三角形区域其中可行解(5，2)和(1，1)分别使目标函数取得最大值和最小值，它们都叫做这个问题的最优解线性规划的有关概念： 2021/

6、8/9 星期一15解线性规划问题的基本步骤： 第一步在平面直角坐标系中画出可行域. 第二步：平移直线 在可行域内找出最优解所对应的点(找使纵截距取得最值时的点). 第三步：解方程组，从而求出目标函数的最大值或最小值简记为: 画.移.求 2021/8/9 星期一16 例1已知x、y满足 ，试求z = 300 x + 900y的最大值典型例题： 分析：先画出平面区域，然后在平面区域内寻找使z = 300 x + 900y取最大值时的点2021/8/9 星期一17 例1已知x、y满足 ，试求z = 300 x + 900y的最大值典型例题： 解：作出可行域，见图中四边形AOBC表示的平面区域x+2y

7、=2502x+y=300 xy250150COBA2021/8/9 星期一18典型例题： 作出直线l0：300 x + 900y = 0，即x + 3y = 0，将它平移至点A，显然，点A的坐标是可行域中的最优解，它使z = 300 x + 900y达到最大值 易得点A(0，125)，所以z max = 3000 + 900125 = 112500l0：x + 3y = 0 xy250150COBAx + 2y = 2502x + y = 3002021/8/9 星期一19典型例题： 变题1：在例1中，若目标函数设为z = 400 x + 300y，约束条件不变，则z的最大值在点C处取得 l0

8、：4x + 3y = 0 xy250150COBAx + 2y = 2502x + y = 300 变题2：若目标函数设为z = 300 x + 600y，约束条件不变，则z的最大值?可在线段AC上任一点处取得2021/8/9 星期一20 事实上，可行域内最优解对应的点在何处，与目标函数z = ax + by(a 0，b 0)所确定的直线l0：ax + by = 0的斜率( )有关 就本例而言，若 = (直线x + 2y = 250的斜率)，则线段AC上所有点都使z取得最大值(如：z = 300 x + 600y时)；2021/8/9 星期一21 当 0时，点A处使z取得最大值(比如：例1)；

9、当 2 时，点C处使z取得最大值(比如：z = 400 x + 300y时)， 其它情况请同学们课外思考2021/8/9 星期一22B Cxyox4y=33x+5y=25x=1 例2：设z2xy,式中变量x、y满足下列条件 求的最大值和最小值。3x+5y25x 4y3x1解：作出可行域如图：当0时，设直线 l0：2xy0 当l0经过可行域上点A时，z 最小，即最大。 当l0经过可行域上点C时，最大，即最小。由 得A点坐标_； x4y3 3x5y25由 得C点坐标_； x=1 3x5y25 zmax2528 zmin214.4 2.4(5,2)(5,2)(1,4.4)(1,4.4)平移l0，平移

10、l0 ，(5,2)2xy0(1,4.4)(5,2)(1,4.4)2021/8/9 星期一23转化转化转化三个转化图解法想一想(结论):线性约束条件可行域线性目标函数Z=Ax+By一组平行线最优解寻找平行线组的 最大（小）纵截距求最值的方法:1,距离法; 2,截距法.2021/8/9 星期一241 （2012年高考（辽宁文理）设变量x,y满足 则2x+3y的最大值为（）A20B35C45D551. 【答案】D 【解析】画出可行域,根据图形可知当x=5,y=15时2x+3y最大,最大值为55,故选D D2021/8/9 星期一252 （2012年高考（天津文）设变量满足约束条件则目标函数的最小值

11、（） A-5B-4C-2D3【解析】做出不等式对应的可行域如图,由图象可知当直线经过点 时,直线的截距最大,而此时最小为,选B. B2021/8/9 星期一263（2012年高考（浙江文）设z=x+2y,其中实数x,y满足, 则z的取值范围是 _.【解析】利用不等式组,作出可行域,可知区域表示的四边形, 但目标函数过点(0,0)时,目标函数最小,当目标函数过点 时最大值为 . 0 , 2021/8/9 星期一27 1. 求z = 600 x + 300y的最大值，使式中的x，y满足约束条件 附加练习 分析：画出约束条件表示的平面区域即可行域再解xyO252100CBA3x + y = 300

12、x + 2y = 2522x + y = 0 z max = 60070 + 30090 = 69000 2021/8/9 星期一28 2. 已知x、y满足不等式组求z = 3x + y的最小值附加练习分析：可先找出可行域,平行移动直线l0：3x + y = 0，找出可行解，进而求出目标函数的最小值.z min = 1 2x + y = 1xy20.5OPx + 2y = 2l0：3x + y = 02021/8/9 星期一29 3满足线性约束条件的可行域内共有_个整数点 4 4设z = x y，式中变量x，y满足求z的最大值和最小值z max = 1， z min = 3附加练习：2021/8/9 星期一30 (1) 求z = 2x + y的最大值，使式中的x、y 满足约束条件附加练习5小结xy(12,12)(-1,-1)(2,-1)2x+y=0 x+y-1=0 x-y=0CBAO21-1-2