新人教版九年级上册初中数学 24.2.2课时3 切线长定理及三角形的内切圆 教学课件

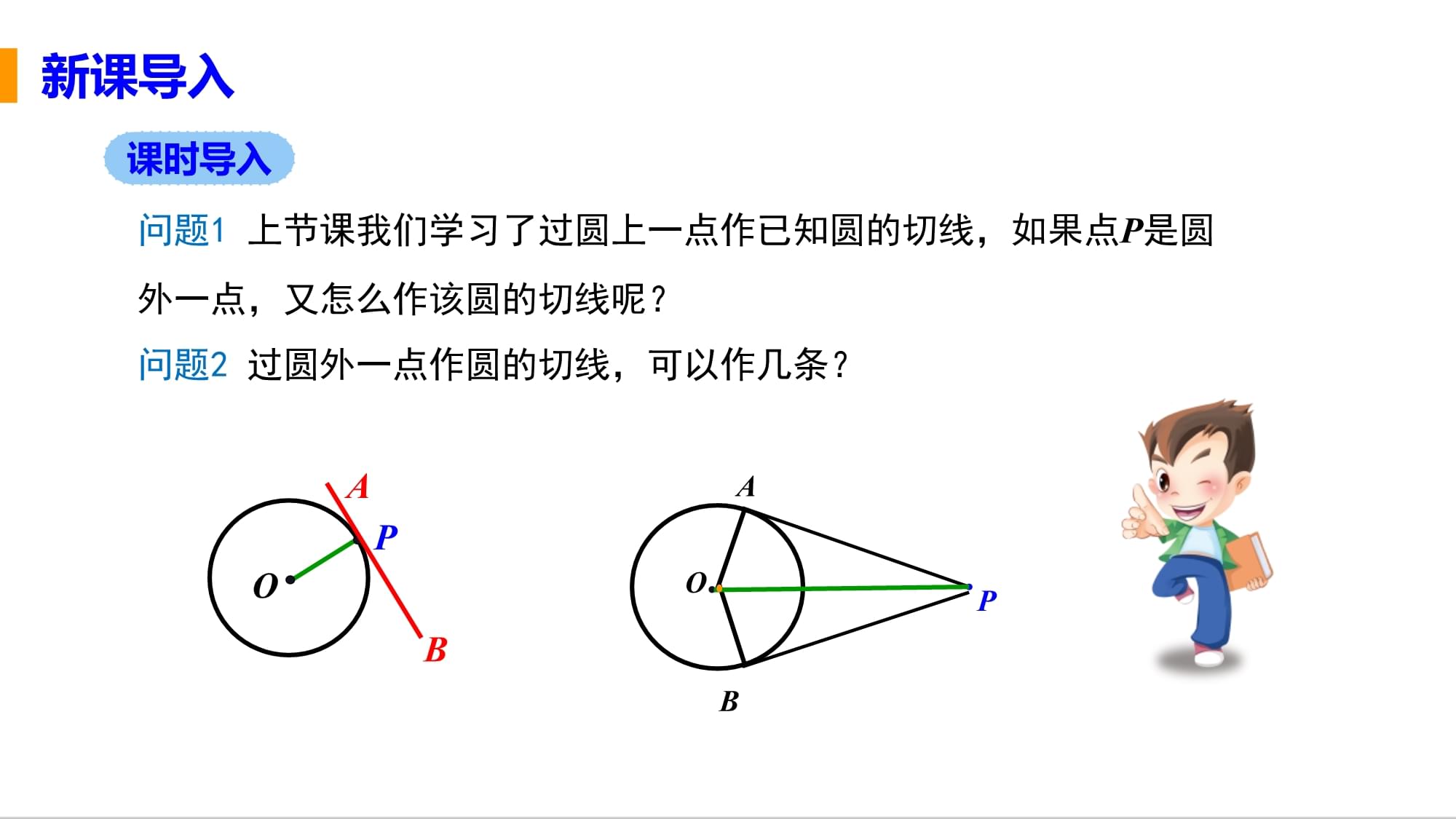
1、第二十四章 圆24.2 点和圆、直线和圆的位置关系24.2.2直线和圆的位置关系课时3 切线长定理及三角形的内切圆1.掌握切线长定理，初步学会运用切线长定理进行计算与证明.（重点）2.了解三角形的内切圆和三角形的内心的概念.3.学会利用方程思想解决几何问题，体验数形结合思想.（难点）学习目标新课导入知识回顾经过半径的外端并且垂直于这条半径的直线是圆的切线.1.切线的判定定理2.切线的性质定理圆的切线垂直于过切点的半径.POO.PBAAB问题1 上节课我们学习了过圆上一点作已知圆的切线，如果点P是圆外一点，又怎么作该圆的切线呢？问题2 过圆外一点作圆的切线，可以作几条？新课导入课时导入新课讲解知

2、识点1 切线长定理一.切线长P1.切线长的定义 经过圆外一点作圆的切线，这点和切点之间的线段的长叫做切线长AO切线是直线，不能度量.切线长是线段的长，这条线段的两个端点分别是圆外一点和切点，可以度量2.切线与切线长的区别新课讲解二.切线长定理问题 在透明纸上画出下图，设PA，PB是O的两条切线，A，B是切点，沿直线OP对折图形，你能猜测一下PA与PB，APO与BPO分别有什么关系吗？PA=PB，APO=BPO.1.切线长定理的内容从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角.PA、PB分别切O于A、BPA = PBOPA=OPB2.几何语言BPOA新课讲解拓

3、展结论PA、PB是O的两条切线，A、B为切点，直线OP交O于点D、E，交AB于点C.（1）写出图中所有的垂直关系；OAPA，OB PB，AB OP.（3）写出图中所有的全等三角形；AOP BOP， AOC BOC， ACP BCP.（4）写出图中所有的等腰三角形.APB AOB（2）写出图中与OAC相等的角；OAC=OBC=APC=BPC.BPOACED切线长问题辅助线添加方法（3）连接圆心和圆外一点.（2）连接两切点；（1）分别连接圆心和切点；新课讲解知识点 1 如图，PA，PB是O的切线，A，B是切点，点C是 AB上一点，过点C作O的切线分别交PA，PB于点 D，E.已知APB60，O的半

4、径为 ，则 PDE的周长为_，DOE的度数为_ 660例新课讲解知识点分析：如图，连接PO，CO，AO，BO，DO，EO，由切 线长定理知PAPB，DCDA，ECEB，因而 PDE的周长可转化为PAPB，即2PA.又由切线 长定理易得DOC AOC，EOC BOC， DOE (AOCBOC) AOB.由 APB60得APO30，又AO ， 由切线的性质得PAO90，PBO90， PO2 ，AOB180APB120. PA 3， DOE AOB60.新课讲解 利用切线长定理进行几何计算时，要注意构成切线长定理的基本图形，作过切点的半径、连接圆外一点与圆心是常用的作辅助线的方法由于切线长定理涉及的

5、线段、角较多，因此熟记基本图形的相关结论是解题的关键，而三角形的有关性质在解决有关切线问题时，也起到了很好的辅助作用新课讲解练一练 下列说法正确的是() A过任意一点总可以作圆的两条切线 B圆的切线长就是圆的切线的长度 C过圆外一点所画的圆的两条切线长相等 D过圆外一点所画的圆的切线长一定大于圆的半径C我们学过的切线，常有 性质：1.切线和圆只有一个公共点；2.切线和圆心的距离等于圆的半径；3.切线垂直于过切点的半径；4.经过圆心垂直于切线的直线必过切点；5.经过切点垂直于切线的直线必过圆心；6.从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角.六个新课讲解新课

6、讲解知识点2 三角形的内切圆问题： 如何作圆，使它和已知三角形的各边都相切？已知：ABC.求作：和ABC的各边都相切的圆.MND作法：（1）作B和C的平分线BM和CN，交点为O.（2）过点O作ODBC, 垂足为D.（3）以点O为圆心，OD为半径作圆O.O就是所求作的圆.ACB新课讲解1.与三角形各边都相切的圆叫做三角形的内切圆.2.三角形内切圆的圆心叫做三角形的内心.3.这个三角形叫做圆的外切三角形.4.三角形的内心就是三角形的三个内角平分线的交点.ACODEF提示：三角形的内心到三角形的三边的距离相等.O是ABC的内切圆，点O是ABC的内心，ABC是O的外切三角形,OD=OE=OF.新课讲解

7、知识点 2 如图，ABC的内切圆O与BC，CA,AB分别相切于点D, E,F,且AB=9，BC=14，CA=13.求AF,BD,CE的长.解：设AF=x，则AE=x. CD=CE=AC-AE=13-x, BD=BF=AB-AF=9-x. 由BD+CD=BC,可得（13-x）+（9-x）=14. 解得x=4. 因此AF=4，BD=5，CE=9.例新课讲解求三角形内切圆的问题，一般的作辅助线的方法为：一是连顶点、内心产生角平分线；二是连切点、内心产生半径及垂直条件.三角形内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心.新课讲解 3 如图，点O是ABC的内切圆的圆心，若BAC 80，则BO

8、C的度数为() A130 B100 C50 D65 分析：由题意知BO，CO分别是ABC，ACB的平分线， OBCOCB (ABCACB) (18080)50， BOC18050130.A例新课讲解名称外心(三角形的外接圆圆心，即三角形三边垂直平分线的交点).内心(三角形的内切圆圆心，即三角形三条角平分线的交点).图形性质三角形的外心到三角形三个顶点的距离相等.三角形的内心到三角形三边的距离相等.位置外心不一定在三角形的内部.内心一定在三角形的内部.角度关系BOC=2A.三角形外心、内心的区别新课讲解练一练如图，已知ABC的内切圆O与BC边相切于点D，连接OB，OD.若ABC=40，则BOD的

9、度数是 .70分析：课堂小结切线长切线长定理作用图形的轴对称性依据提供了证线段和角相等的方法辅助线分别连接圆心和切点；连接两切点；连接圆心和圆外一点.三角形内切圆运用切线长定理，将相等线段转化到某条边上，从而建立方程，求线段的长.有关概念内心、三角形的内切圆、圆的外切三角形应用重要结论只适合于直角三角形当堂小练1.如图，ABC的内切圆O与BC，CA，AB分别相切于点D，E，F，且AB=11cm，BC=14cm，CA=13cm，则AF的长为( )A.3cmB.4cm C.5cmD.9cmC当堂小练2.如图，已知VP、VQ为T的切线，P、Q为切点，若VP=3cm，则VQ= cm.若PVQ60，则T的半径PT cm.3当