机械工程控制基础(第5章 系统的稳定性).

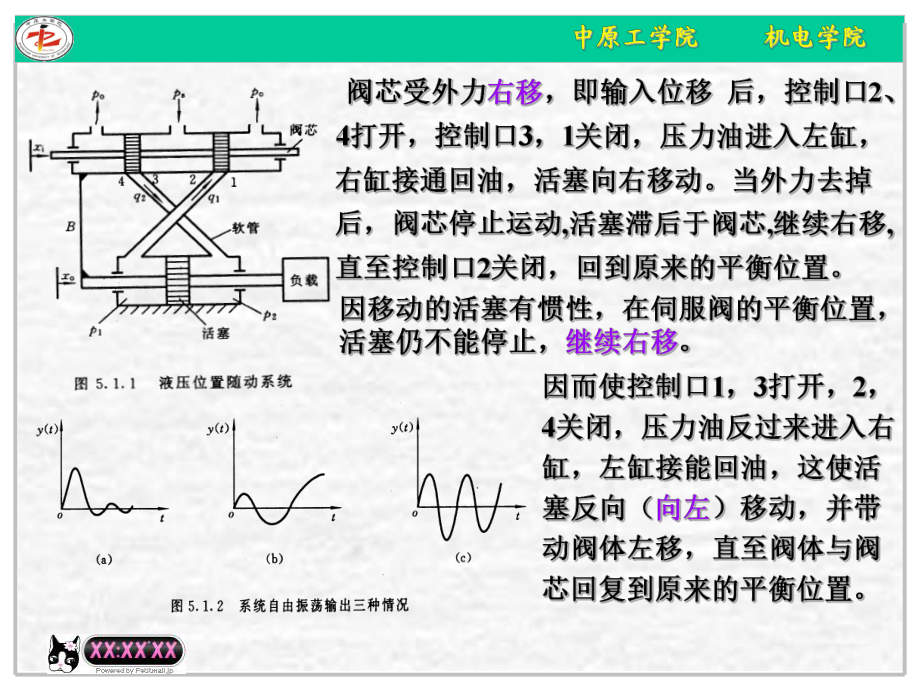
1、12,q qix0 x ix( )E s 第三，控制理论中所讨论的稳定性其实都是指自由振荡下的稳定性。第三，控制理论中所讨论的稳定性其实都是指自由振荡下的稳定性。即讨论即讨论输入为零，系统仅存在有初始状态不为零时输入为零，系统仅存在有初始状态不为零时的稳定性，即的稳定性，即 讨论系统自由振荡是收敛的还是发散的；讨论系统自由振荡是收敛的还是发散的；或者：讨论或者：讨论系统初始状态为零时，系统脉冲响应是收敛的还是发散系统初始状态为零时，系统脉冲响应是收敛的还是发散的的。 至于用激振或加外力方法施以强迫振动或运动，因而造成系统共振至于用激振或加外力方法施以强迫振动或运动，因而造成系统共振（或称谐振）

2、或偏离平衡位置越来越远，这不是控制理论所要讨论（或称谐振）或偏离平衡位置越来越远，这不是控制理论所要讨论的稳定性。的稳定性。 若系统在初始状态下（不论是无输入时的初态，还是输入引起若系统在初始状态下（不论是无输入时的初态，还是输入引起的初态，还是两者之和）的时间响应随着时间的推移，的初态，还是两者之和）的时间响应随着时间的推移，逐渐衰减并逐渐衰减并趋向于零（即回到平衡位置），则称该系统为稳定的趋向于零（即回到平衡位置），则称该系统为稳定的； 反之，若在初始状态影响下，由它所引起的系统的时间响应反之，若在初始状态影响下，由它所引起的系统的时间响应随随时间的推移而发散（即偏离平衡位置越来越远），则

3、称该系统为不时间的推移而发散（即偏离平衡位置越来越远），则称该系统为不稳定的稳定的。 根据上述稳定性的定义，可以用下述两种方法，分别求得根据上述稳定性的定义，可以用下述两种方法，分别求得定常线定常线性系统稳定性条件性系统稳定性条件。方法方法(1)：设定常线性系统的微分方程为：设定常线性系统的微分方程为： 式中，式中， 若记若记 并对式（并对式（5.1.1）作）作Laplace变换，得变换，得 式中式中 为系统传递函数。为系统传递函数。1110()( )nnnna papa pa x t10() ( ),mmib pb pb x t,nm（5.1.1） ,dpdt1110( );nnnnD pa

4、 papa pa1110( ),mmmmM pb pbpb pb( )( )( )( ),( )( )iM sN sXsX sD sD s（5.1.2） ( )( )( )M sG sD s 是与初始条件是与初始条件 输出输出 及其各阶导数及其各阶导数 在输入作在输入作用前用前 时刻的值，即系统在输入作用前的初始状态时刻的值，即系统在输入作用前的初始状态 有关的多项式。有关的多项式。研究初始状态研究初始状态 影响下系统的时间响应时，可在式（影响下系统的时间响应时，可在式（5.1.25.1.2）中）中取取 得到这一时间响应（即零输入的响应）：得到这一时间响应（即零输入的响应）： 若若 为系统特征

5、方程为系统特征方程 的根（或称系统的特征根，亦即系统的根（或称系统的特征根，亦即系统的传递函数的极点），当的传递函数的极点），当 ( )( )各不相同时，有：各不相同时，有：( )N s( )N s( )(0 )kx( )x t( )( )kxt0t ( )0iX s ( )( )( )N sXsD s( )0D s 12;in， ， ，isis1111( )( )( )exp()( )niiiN sX tLXsLAstD s1( ),( )( )( )issiN sdAD sD sdsD s式中，式中，（5.1.3） islim( )0otx tlim( )otx t 上述结论对于任何初始状

6、态上述结论对于任何初始状态（只要不使系统超出其（只要不使系统超出其线性线性工作范工作范围）围）都是成立的，都是成立的，而且当系统的特征根具有相同值时，也是成立的。而且当系统的特征根具有相同值时，也是成立的。 式（式（5.1.1）右端各项系数，对系统稳定性没有影响，）右端各项系数，对系统稳定性没有影响，相当于系统相当于系统传递函数传递函数G(s)的各零点的稳定性没有影响。的各零点的稳定性没有影响。 这些参数反映系统与外界作用的关系，反映了外界输入作用这些参数反映系统与外界作用的关系，反映了外界输入作用于同一系统的不同处的特性，不影响于同一系统的不同处的特性，不影响系统稳定性系统稳定性这个系统本身

7、的固这个系统本身的固有特性。有特性。方法方法(2)：若对线性系统在初始状态为零时输入单位脉冲函数：若对线性系统在初始状态为零时输入单位脉冲函数 （这（这实际上是瞬间干扰），使系统具有一个初态。再由此初态出发，可实际上是瞬间干扰），使系统具有一个初态。再由此初态出发，可得到一个输出，即单位脉冲响应得到一个输出，即单位脉冲响应 的形式与零输入响应的形的形式与零输入响应的形式相同，式相同，显然，显然， 则系统稳定；则系统稳定； 则系统不稳定则系统不稳定 。( ) t( )( )tt。lim( )0,tt若lim( ),tt 若因为因为( ) ( )( )( ),( )M sLtW sG sD s11

8、( )( ) ( ),( )M stLL sLD s(5.1.4) 因此系统的单位脉冲响应因此系统的单位脉冲响应211( )( )exp()exp().( )inniiiiis sM ststAstD s（5.1.5） 这一结论与第三章有关结论是一致的，可见只有当这一结论与第三章有关结论是一致的，可见只有当 系统的系统的全部特征根都具有负实部时，才有全部特征根都具有负实部时，才有(1,2, )is inlim( )0tt 。 无论是无论是无输入时的初态无输入时的初态或或输入所引起的初态输入所引起的初态，或，或只是输入所引只是输入所引起的初态起的初态，则系统是否稳定应由此时的，则系统是否稳定应由

9、此时的过渡过程随着时间的推移是过渡过程随着时间的推移是否收敛至一个稳态响应来决定否收敛至一个稳态响应来决定，而这是与本小节开始时讲的系统的，而这是与本小节开始时讲的系统的稳定性的定义是一致的；稳定性的定义是一致的； 过渡过程是否收敛也仅仅取决于系统的全部特征根是否都具有过渡过程是否收敛也仅仅取决于系统的全部特征根是否都具有负实部负实部。 系统稳定的充要条件为：系统稳定的充要条件为：系统的全部特征根都具有负实部；反之，系统的全部特征根都具有负实部；反之，若特征根中只要有一个或一个以上具有正实部，则系统必不稳定。若特征根中只要有一个或一个以上具有正实部，则系统必不稳定。 也就是说，若系统传递函数也

10、就是说，若系统传递函数 的全部极点均位于的全部极点均位于s平面的左半平面的左半平面，则系统稳定；反之，若有一个或一个以上的极点位于平面，则系统稳定；反之，若有一个或一个以上的极点位于s平面平面的右半平面，则系统不稳定；的右半平面，则系统不稳定；若有部分极点位于虚轴上，而其余的若有部分极点位于虚轴上，而其余的极点均在极点均在s平面的左半平面，则系统称为临界稳定，即平面的左半平面，则系统称为临界稳定，即 趋于等幅谐波振荡。趋于等幅谐波振荡。 ( )G s( )( )x tt或 由于对系统参数的估算或测量可能不够准确，而且系统在实际由于对系统参数的估算或测量可能不够准确，而且系统在实际运行过程中，参

11、数值也可能有变动，因此原来处于虚轴上的极点实运行过程中，参数值也可能有变动，因此原来处于虚轴上的极点实际上可能变动到际上可能变动到s平面的右半面，致使系统不稳定。平面的右半面，致使系统不稳定。从工程控制的从工程控制的实际情况看，一般认为临界实际上往往属于不稳定实际情况看，一般认为临界实际上往往属于不稳定。 应当指出，上述不稳定区虽然包括虚轴应当指出，上述不稳定区虽然包括虚轴 ，但不包括虚轴所通但不包括虚轴所通过的坐标原点。这一点上过的坐标原点。这一点上, 相当于特征方程之根相当于特征方程之根 ，系统仍属稳定，系统仍属稳定。j0is 这也就是说，若要求系统的输出不能超出任意给定的正数，能在初这也

12、就是说，若要求系统的输出不能超出任意给定的正数，能在初态为态为 式中式中 则系统称为在则系统称为在意义下稳定；反之，若要意义下稳定；反之，若要求系统的输出不能超出任意给定的求系统的输出不能超出任意给定的正数正数 ，但却不能找到不为零的，但却不能找到不为零的正数正数 来满足式来满足式(5.1.6)，则系统称为在，则系统称为在意义下不稳定。意义下不稳定。( )( )(0),( )(0),kkxxtt 的情况下 满足输出为 (5.1.6)0,1,2,k 渐近稳定性渐近稳定性就是前面对线性系统定义的稳定性，它要求由就是前面对线性系统定义的稳定性，它要求由初态初态引起的响应最终衰减到零引起的响应最终衰减

13、到零，一般所讲的线性系统的稳定性，也就是，一般所讲的线性系统的稳定性，也就是渐近稳定性，当然，也是渐近稳定性，当然，也是意义下的稳定性；但对非线系统意义下的稳定性；但对非线系统而言，这两种稳定性是不同的。而言，这两种稳定性是不同的。 比较渐近稳定性与比较渐近稳定性与意义下的稳定性可知，前者比后者意义下的稳定性可知，前者比后者对系统的稳定性的要求高，系统若是渐近稳定的则一定是对系统的稳定性的要求高，系统若是渐近稳定的则一定是意义下稳定的，反之则不尽然。意义下稳定的，反之则不尽然。 “小偏差小偏差”稳定性又称稳定性又称“小稳定小稳定”或或“局部稳定性局部稳定性”。由于实际。由于实际系统往往存在非线

14、性，因此系统的动力学方程往往是建立在系统往往存在非线性，因此系统的动力学方程往往是建立在“小偏差小偏差”线性化的基础之上的。在偏差较大时，线性化带来的误差太大，因此，线性化的基础之上的。在偏差较大时，线性化带来的误差太大，因此，用线性化方程来研究的稳定性时，就只限于讨论初始偏差（初态）不用线性化方程来研究的稳定性时，就只限于讨论初始偏差（初态）不超出某一微小范围时的稳定性，称之为超出某一微小范围时的稳定性，称之为“小偏差小偏差”稳定性稳定性。初始偏差。初始偏差大时，就不能用来讨论系统的稳定性。大时，就不能用来讨论系统的稳定性。判别系统的稳定性，也就是要解出系统特征方程的根，看这些根是判别系统的

15、稳定性，也就是要解出系统特征方程的根，看这些根是否均具有负实部。否均具有负实部。在实际工程系统中，根的求解就较困难，通过讨论在实际工程系统中，根的求解就较困难，通过讨论特征根的分布特征根的分布，看其是否全部具有负实部，以此来看其是否全部具有负实部，以此来判别系统的稳定性，判别系统的稳定性，由此形成了由此形成了一系列一系列稳定性判据。稳定性判据。其中最重要的一个判据就是其中最重要的一个判据就是1884年由年由E.J.Routh提出的提出的Routh判据判据。Routh判据是基于判据是基于方程根和系数的关系建立方程根和系数的关系建立的，它是判别系统稳定性的，它是判别系统稳定性的的充要充要条件条件-

16、代数判据代数判据。设系统特征方程为：设系统特征方程为：将式（将式（5.2.1）中各项同除以）中各项同除以an并分解因式，得并分解因式，得式中，式中， 为系统的特征根，再将式（为系统的特征根，再将式（5.2.2）右边展开，得右边展开，得:1110( )0nnnnD sa sasa sa110112()()(),nnnnnnnaaasssssssssaaa12,ns ss121()()()()nnssssssss121112()()( 1)nnnnnnnijiiijiijssi ss s ss （5.2.1） （5.2.2）（5.2.3）比较式（比较式（5.2.2）与式（）与式（5.2.3）可看出

17、根与系数有如下的关系：）可看出根与系数有如下的关系：（5.2.4） niinnsaa11njijinnjissaa2, 12nkjikjinnkjisssaa3,2, 13ininnsaa101 按习惯，一般取按习惯，一般取 为正值，因此，为正值，因此，上述两个条件可归结为系统稳定上述两个条件可归结为系统稳定的一个必要条件，即的一个必要条件，即当然，由式（当然，由式（5.2.4）还可看出，仅仅有各项系数）还可看出，仅仅有各项系数 ,还不一定能还不一定能判定判定 均具有负实部，也就是说，均具有负实部，也就是说，系统要稳定，必须满系统要稳定，必须满足式（足式（5.2.5）；而满足）；而满足(5.2

18、.5），），系统可能稳定，也可能不稳定。系统可能稳定，也可能不稳定。 从式（从式（5.2.4）可知，）可知，要使全部特征根要使全部特征根 均具有负实部，均具有负实部，就必就必须满足以下两个条件须满足以下两个条件，即系统稳定的必要条件，即系统稳定的必要条件:(1)特征方程的各项系数特征方程的各项系数 都不等于零，都不等于零，因为若有一因为若有一系数为零，则必出现实部为零的特征根或实部有正有负的特征根，才系数为零，则必出现实部为零的特征根或实部有正有负的特征根，才能满足式（能满足式（5.2.4）中各式。）中各式。 (2)特征方程的各项系数特征方程的各项系数 的符号都相同，的符号都相同，这样才能满足

19、式这样才能满足式(5.2.4)中各式。中各式。 12,ns ss(0,1,2,1, )ia inniaia1100,0,.,0,0.nnaaaa（5.2.5） 0ia 12,ns ss1. Routh表表（1）将系统的特征方程式（）将系统的特征方程式（5.2.1）的系数按下列形式排成两行：）的系数按下列形式排成两行： （2）列）列Routh计算表：如以六阶特征方程为例，设：计算表：如以六阶特征方程为例，设：则有：则有： 246nnnnaaaa 1357nnnnaaaa654326543210( )0sD sa sa sa sa sa saa 高于高于6 6阶时阶时( (一般不会一般不会) )，

20、见课本上通式，见课本上通式。 （3 3）若上表）若上表第一列中各元的符号都相同第一列中各元的符号都相同，即第一列各元间依次序数，即第一列各元间依次序数下来，下来，符号的改变次数为零，则具有正实部特征根的个数等于零，符号的改变次数为零，则具有正实部特征根的个数等于零，系统是稳定的；若第一列各元符号不同，则系统是不稳定的系统是稳定的；若第一列各元符号不同，则系统是不稳定的，其各，其各元间元间符号依序改变的次数符号依序改变的次数等于具有正实部特征根的等于具有正实部特征根的个数个数。2. Routh稳定判据稳定判据 根据根据Routh所表述条件，所表述条件，“Routh判据判据”即表示为：即表示为：“

21、系统稳定系统稳定充要条件是，充要条件是，Routh表中第一列各元的符号均为正，且值不为表中第一列各元的符号均为正，且值不为零。零。” 【例1】：系统的特征方程 0301119234sssssD0030001230301113003030111119101113019101234sssss第一列各元符号改变次数为2，因此：（1）系统不稳定；（2）系统有两个具有正实部的特征根。（改变符号一次）（改变符号一次）（改变符号一次）（改变符号一次）【例2】：已知 ，试确定K取何值时，系统方能稳定。0.286.6及 2223202nnnniKsssKssXsXsG 022223nnnKssssD 07500

22、75006 .3423KssssD闭环传递函数闭环传递函数闭环传递函数的特征方程为闭环传递函数的特征方程为代入参数值代入参数值 0750075006 .3423KssssD0750006 .34750075006 .34075006 .340750010123KKKssss（1）7500K0, 亦即K006 .34750075006 .34K6 .34K（2）故能使系统稳定的参数K的取值范围为：0K0，表示，表示LF按顺时针方向包围原点按顺时针方向包围原点N次；次； N0，表示，表示LF按逆时针方向包围原点按逆时针方向包围原点N次；次； N=0，表示，表示LF不包围原点。不包围原点。(1,2,

23、 )ip inip 应用幅角原理不能单独确定出包围应用幅角原理不能单独确定出包围Ls内的函数内的函数F(s)的零点数的零点数Z或其极或其极点数点数P，而仅能确定他们之间的差值，而仅能确定他们之间的差值(Z-P)。 Gk(s)的极点就等于的极点就等于F(s)函数的极点，函数的极点，因此因此，若已知系统的，若已知系统的Gk(s)，就，就可直接求得可直接求得P。若又能在若又能在F(s)平面上确定出平面上确定出LF曲线包围原点的圈数曲线包围原点的圈数N，则可由则可由Z=N+P计算出在计算出在s平面上包围于封闭曲线平面上包围于封闭曲线LS中的中的F(s)的零的零点数点数Z，这些零点也就是这些零点也就是G

24、B(s)相应的极点。相应的极点。 曲线曲线LS LF的形状对于的形状对于N，Z，P的数值是没有关系的，即的数值是没有关系的，即LF绕原点绕原点的圈数的圈数N仅取决于仅取决于LS所包围的所包围的F(s)的零点和极点的数目的零点和极点的数目，而与，而与LS的形的形状无关。状无关。LF, LS也称为也称为Nyquist轨迹。轨迹。 定常线性系统稳定的充要条件是，其定常线性系统稳定的充要条件是，其闭环系统的特征方程闭环系统的特征方程1+G(s)H(s)=0的全部根具有负实部的全部根具有负实部，即在，即在s平面的右半平面平面的右半平面系系统没有极点统没有极点，亦即，亦即F(s)在在s平面的右半平面平面的

25、右半平面没有零点没有零点（Z=0）。）。1、 s平面上的平面上的Nyquist轨迹轨迹 s平面上的平面上的Nyquist轨迹如图轨迹如图5.3.3（a）所示。）所示。 设在设在s平面上有封闭曲线平面上有封闭曲线LS，其中其中(1)，(2)两段是由两段是由 =-到到+的整个虚轴组成的，的整个虚轴组成的，(3)段是由半径段是由半径R趋于无穷大的圆弧组趋于无穷大的圆弧组成的成的。因此，。因此，(1)，(2)，(3)段就封闭地包围了整个段就封闭地包围了整个s平面的右半平面平面的右半平面，由于在应用幅角原理时，由于在应用幅角原理时，LS不能通过不能通过F(s)函数的任何极点。所以函数的任何极点。所以当函

26、当函数数F(s)有若干个极点处于有若干个极点处于s平面的虚轴或原点上时，平面的虚轴或原点上时，LS应被认为是以应被认为是以这些点为圆心，以无穷小为半径的圆弧按反时针方向从这些点的右侧这些点为圆心，以无穷小为半径的圆弧按反时针方向从这些点的右侧绕过绕过，如小段圆弧，如小段圆弧(4)与与(4)所示。由于所示。由于(4)，(4)紧贴极点绕过，因此，紧贴极点绕过，因此，可以认为可以认为LS曲线包围了整个曲线包围了整个s平面的右半平面平面的右半平面。这一。这一LS封闭曲线即为封闭曲线即为s平面上的平面上的Nyquist轨迹轨迹。当当 由由-变到变到+时，轨迹的方向为顺时针方向。时，轨迹的方向为顺时针方向

27、。2、 F平面上的平面上的Nyquist轨迹轨迹 F平面上的平面上的Nyquist轨迹轨迹（F平面即平面即F(s)平面的简定）平面的简定）按按F(s)函数函数作出作出。若其图形如图。若其图形如图5.3.3(b)所示，则其曲线不包围原点，即所示，则其曲线不包围原点，即N=0，说，说明相应的明相应的Ls曲线所包围的曲线所包围的F(s)函数的极点数与零点数相等，故其差值函数的极点数与零点数相等，故其差值为零（为零（N=Z-P=0）。）。 注意：这里所说的注意：这里所说的Z，P是指包围于图是指包围于图5.3.3(a)上上Ls曲线中的曲线中的F(s)位于位于s平面的右半平面的零、极点数，不是指平面的右半

28、平面的零、极点数，不是指F(s)函数所有的零点数和极函数所有的零点数和极点数点数。由前述可知，系统稳定的充要条件是。由前述可知，系统稳定的充要条件是Z=0。判别判别Z=0，不是在，不是在s平面上进行，而是转化到平面上进行，而是转化到F平面上进行。平面上进行。 由由F平面上的平面上的Nyquist轨迹轨迹LF可知，若它包围原点可知，若它包围原点N圈，则可知圈，则可知N。另。另外，由已知的外，由已知的F(s)函数，可以先求得函数，可以先求得F(s)位于位于s平面的右半平面的极平面的右半平面的极点数点数P，从而可求得，从而可求得Z=N+P，为保证系统稳定，应使为保证系统稳定，应使Z=0，即，即 N=

29、Z-P=-P 也就是，也就是，当当F平面的平面的Nyquist轨迹轨迹LF逆时针包围原点的圈数逆时针包围原点的圈数N等于等于F(s)函数位于函数位于s平面的右半平面的极点数平面的右半平面的极点数P时，系统稳定。时，系统稳定。3、 GH平面上的平面上的Nyquist轨迹轨迹GH平面（即平面（即G(s)H(s)平面的简写）上的情况与此相似。因平面的简写）上的情况与此相似。因F(s)=1+G(s)H(s)，即，即G(s)H(s)=F(s)-1GH平面只不过是将平面只不过是将F平面的虚轴右移了平面的虚轴右移了1个单位之后所构成的新复个单位之后所构成的新复平面。平面。GH平面上的（平面上的（-1,j0）

30、点就是）点就是F平面上的原点平面上的原点。所以，在。所以，在GH平面上，包围点（平面上，包围点（-1, j0）的圈数）的圈数N，就等于在，就等于在F平在上平在上LF包围原点包围原点的圈数的圈数N，其关系如图，其关系如图5.3.3(b)，(c)所示。所示。GH平面的平面的Nyquist轨迹，轨迹，如图如图5.3.3(s)所示，它的相应的所示，它的相应的s平面的平面的Nyquist轨迹如图轨迹如图5.3.3(a)所示。所示。 由于任何物理上可实现的开环系统，其的分母的阶次由于任何物理上可实现的开环系统，其的分母的阶次n必不小于分于必不小于分于的阶系，故有：的阶系，故有： 和和 当然，当然，s或或s

31、0，均指其模而言。所以，均指其模而言。所以，s平面上半径为平面上半径为的半圆的半圆映射到映射到GH平面上为原点或实轴上的一点；平面上为原点或实轴上的一点；s平面上的原点映射到平面上的原点映射到GH平面上为半径平面上为半径的半圆弧（当分母含有积分环节时）。的半圆弧（当分母含有积分环节时）。 0,lim( ),KsnmGsnm当常量 当0,lim( ),KsGs当分母中含有积分环节时常量 当分母中不含有积分环节时因为因为LS表示：表示：s平面上平面上 中实部中实部 为零，为零， 由由-变到变到+时时s的轨迹（即虚轴），再加上半径为的轨迹（即虚轴），再加上半径为的半圆弧；而的半圆弧；而s平面上半径为

32、平面上半径为 的半圆弧映射到的半圆弧映射到GH平面上只是一个点，它对于平面上只是一个点，它对于G(s)H(s)包围某点的包围某点的情况无影响，所以情况无影响，所以G(s)H(s)的绕行情况只需考虑的绕行情况只需考虑s平面的平面的j 轴映射到轴映射到GH平面上的开环平面上的开环Nyquist轨迹轨迹G(s)H(s)即可即可。sj GH平面上系统稳定的充要条件可表述为：平面上系统稳定的充要条件可表述为：若当若当GH平面上平面上Gk(s)，即，即G(s)H(s)的的Nyquist轨迹逆时针包围点（轨迹逆时针包围点（-1, j0）的圈数）的圈数N，等于，等于Gk(s)在在s平面的右半平面的极点数平面的

33、右半平面的极点数P时，则闭环系时，则闭环系统稳定，统稳定，因为此时因为此时N=-P，由，由N=Z-P知知Z=0。 这一充要条件也可表述为：这一充要条件也可表述为：当当 由由-到到+时，若时，若GH平面上的开环平面上的开环频率特性频率特性Gk(s)即即G(j ）顺时针方向包围点（顺时针方向包围点（-1, j0）P圈（圈（P为为Gk(s)在在s平面的右半平面的极点数平面的右半平面的极点数P ），则闭环系统稳定。），则闭环系统稳定。 这一表述就是这一表述就是Nyquist稳定判据。稳定判据。 在应用在应用Nyquist判据时，首先要知道系统的判据时，首先要知道系统的GK(s) 在在s平面上的右半平平

34、面上的右半平面的极点数面的极点数P，然后分下述两种情况来判别：，然后分下述两种情况来判别： （1）当当P=0和和 从从-变到变到+时，若时，若GH平面上的平面上的G(j )H(j )不包围不包围点（点（-1, j0），即），即N=0，则闭环系统稳定；反之，则闭环系统不稳定。，则闭环系统稳定；反之，则闭环系统不稳定。 （2）当当P0和和 从从-变到变到+时，若时，若GH平面上的逆时针包围点平面上的逆时针包围点(-1, j0)P圈，则闭环系统稳定；若逆时针包围点（圈，则闭环系统稳定；若逆时针包围点（-1, j0）的圈数不到）的圈数不到P圈圈（表示（表示ZP），则闭环系统），则闭环系统不稳定。不稳定

35、。 当系统中串联有积分环节时，开环传递函数当系统中串联有积分环节时，开环传递函数GK(s)有位于平面坐标有位于平面坐标原点处的极点。应用原点处的极点。应用Nyquist判据时，由于平面上的判据时，由于平面上的Nyquist轨迹轨迹LS不能经过不能经过GK(s) 的极点，故应以半径为无穷小的圆弧的极点，故应以半径为无穷小的圆弧(r0) 逆时针逆时针绕过开环极点所在的原点，如图绕过开环极点所在的原点，如图5.3.3(a)所示。这时开环传递函数所示。这时开环传递函数在在s平面的右半平面上的极点数已不再包含原点处的极点。平面的右半平面上的极点数已不再包含原点处的极点。 设开环传递函数为：设开环传递函数

36、为：式中，式中，v为系统中串联积分环节的个数。当为系统中串联积分环节的个数。当s沿无穷小半圆逆时针方向沿无穷小半圆逆时针方向移动时，有：移动时，有：映射到映射到GH平面上的平面上的Nyquist轨迹为：轨迹为：因此，当因此，当s沿小半圆从沿小半圆从 =0-变化到变化到 =0+ 时，时， 角从角从 经经0变化变化到到 ，这时这时GH平面上的平面上的Nyquist轨迹将沿无穷大半径按顺时针方向轨迹将沿无穷大半径按顺时针方向从从 到到 。0limjrsre001lim01lim(1)( )( )lim(1)jrjrmjjjnsrerjisreKT sKG s H sersT s22211(1)( )

37、( )(1)mjjnjiKT sG s H ssT s2 1） Nyquist判据并不是在判据并不是在s平面而是平面而是GH平面判别系统的稳定性。平面判别系统的稳定性。 通过幅角原理将通过幅角原理将s平面的平面的Nyquist轨迹（虚轴）映射为轨迹（虚轴）映射为GH平面上的平面上的Nyquist轨迹轨迹G(j )H(j ) ，然后根据，然后根据G(j )H(j )轨迹包围点（轨迹包围点（-1,j0）的）的情况来判别闭环系统的稳定性，而情况来判别闭环系统的稳定性，而G(j )H(j )正是系统的正是系统的Gk(j ) 。2） Nyquist判据的证明虽较复杂，但应用简单判据的证明虽较复杂，但应用

38、简单.由于一般系统的开环系统多为最小相位系统，由于一般系统的开环系统多为最小相位系统，P=0，故只要看开环，故只要看开环Nyquist轨迹是否包围点（轨迹是否包围点（-1,j0），若不包围，系统就稳定。），若不包围，系统就稳定。当开环系统为非最小相位系统，当开环系统为非最小相位系统，P0先求出其先求出其P，再看开环，再看开环Nyquist轨轨迹包围点（迹包围点（-1,j0）的圈数，并注意）的圈数，并注意 由小到大时轨迹的方向，若是逆由小到大时轨迹的方向，若是逆时针包围点（时针包围点（-1,j0）P圈，则系统稳定。圈，则系统稳定。 3）在）在P=0，即，即Gk(j )在在s平面的右半平面无极点时

39、，按习惯有时称平面的右半平面无极点时，按习惯有时称为开环稳定；为开环稳定；在在P0，即开环传递函数在，即开环传递函数在s平面的右半平面有极点时，按习惯有平面的右半平面有极点时，按习惯有时称为开环不稳定，有的书上介绍的就是首先判明开环是否稳定，时称为开环不稳定，有的书上介绍的就是首先判明开环是否稳定，亦即先确定亦即先确定P的数值，然后再用的数值，然后再用Nyquist判据来判别闭环系统的稳定判据来判别闭环系统的稳定性。性。开环不稳定，闭环仍可能稳定；开环稳定，闭环也可能不稳定。开环不稳定，闭环仍可能稳定；开环稳定，闭环也可能不稳定。 4） 开环开环Nyquist轨迹对实轴是对称的轨迹对实轴是对称

40、的,因为当因为当+ 变为变为- 时时,G(-j )H(-j )与与G(j )H(j )的模相同，而相位异号，即：的模相同，而相位异号，即： 所以，所以， 由由-到到0与与 由由0到到+的开环的开环Nyquist轨迹对实轴对称。因而轨迹对实轴对称。因而一般只需绘出一般只需绘出 由由0到到 +的曲线即可判别稳定性。的曲线即可判别稳定性。Nyquist轨迹在轨迹在 由由0到到+时，包围点（时，包围点（-1,j0）一圈，故已可知）一圈，故已可知 由由-到到+时共包围时共包围点（点（-1,j0）两圈，所以系统不稳定。）两圈，所以系统不稳定。|()()| |()()|GjHjG jH j()()()()G

41、jHjG jH j 系统传递函数的分母反映了系统本身的固有特性，现在闭环系系统传递函数的分母反映了系统本身的固有特性，现在闭环系统的传递函数的分母是统的传递函数的分母是1+G(s)H(s)，即，即F(s)，而，而F(s)包围包围F平面上原平面上原点的情况与点的情况与G(s)H(s)包围包围GH平面上点平面上点(-1，j0)的情况完全一样，因的情况完全一样，因此，此，G(s)H(s)这一开环传递函数包围这一开环传递函数包围GH平面上点平面上点(-1，j0)的情况就的情况就反映了闭环系统的固有特性。反映了闭环系统的固有特性。 因此，用它来判别系统的稳定性，即由因此，用它来判别系统的稳定性，即由Ny

42、quist判据用开环传递判据用开环传递函数判别闭环系统的稳定性，从物理意义上来说也是容易解释的。函数判别闭环系统的稳定性，从物理意义上来说也是容易解释的。 延时环节是线性环节，延时环节是线性环节， 但用劳斯判据难以进行判断，现分析延但用劳斯判据难以进行判断，现分析延时环节串联或并联在闭环系统的前向通道中的情况。时环节串联或并联在闭环系统的前向通道中的情况。1.1.延时环节串联在闭环系统的前向通道中时系统的稳定性延时环节串联在闭环系统的前向通道中时系统的稳定性 图图5.3.165.3.16所示为一具有延时环节的系统方框图，其所示为一具有延时环节的系统方框图，其中中G G1 1( (s s) )是

43、除延时环节以外的开环传递函数，这时整是除延时环节以外的开环传递函数，这时整个系统的开环传递函数为：个系统的开环传递函数为： 其开环频率特性，幅频特性和相频特性分别为：其开环频率特性，幅频特性和相频特性分别为： 由此可见，由此可见，延时环节不改变原系统的幅频特性，而延时环节不改变原系统的幅频特性，而仅仅使相频特性发生变化仅仅使相频特性发生变化。1( )( )sKGsG s e1()(),jKGjGje1()() ,KGjGj1()(KGjG j 例如，在图例如，在图5.3.165.3.16所示系统中，若所示系统中，若则开环传递函数和开环频率特性分别为：则开环传递函数和开环频率特性分别为：其开环其

44、开环NyquistNyquist图如图图如图5.3.175.3.17所示。所示。11( ),(1)G ss s1( ),(1)skG ses s， 1()(1)jKGjejj 由图由图5.3.175.3.17可见，当可见，当 ，即无延时环节时，即无延时环节时，NyquistNyquist轨迹的相位不超过轨迹的相位不超过180180度，只到第三度，只到第三象限，此二阶系统肯定是稳定的。随着象限，此二阶系统肯定是稳定的。随着 值增值增加，相位也增加，加，相位也增加，NyquistNyquist轨迹向左上方偏转，轨迹向左上方偏转，进入第二和第一象限，当进入第二和第一象限，当 增加到使增加到使Nyqu

45、istNyquist轨轨迹包围点（迹包围点（1,j01,j0）时，闭环系统就不稳定。）时，闭环系统就不稳定。所以，由开环所以，由开环NyquistNyquist图上可以明显看出，串联图上可以明显看出，串联延时环节对稳定性是不利的，延时环节对稳定性是不利的，虽然一阶系统或二阶系统，其开环放大系数虽然一阶系统或二阶系统，其开环放大系数K K就不就不允许取很高的数值，同时，为了提高这些系统允许取很高的数值，同时，为了提高这些系统的稳定性，还应尽可能地减小延时时间的稳定性，还应尽可能地减小延时时间 。 0 Nyquist判据判据:利用开环频率特性的极坐标图（利用开环频率特性的极坐标图（Nyquist图

46、）来判别闭环系统稳定性。图）来判别闭环系统稳定性。利用开环对数坐标图，即利用开环对数坐标图，即Bode图，来判别系统的稳定图，来判别系统的稳定性。这种方法有时称为对数频率特性判据，简称对性。这种方法有时称为对数频率特性判据，简称对数判据或数判据或Bode判据。判据。它实质上是它实质上是Nyquist判据的引申。判据的引申。 开环开环BodeBode图与开环极坐标图对应关系图与开环极坐标图对应关系： （1 1）极坐标图上的单位圆相当于）极坐标图上的单位圆相当于BodeBode图上的图上的0 0分贝线，分贝线，即对数幅频特性图的横轴。即对数幅频特性图的横轴。 （2 2）极坐标图上的负实轴相当于）极

47、坐标图上的负实轴相当于BodeBode图上的图上的180180线，线，即对数相频特性图的横轴。相位即对数相频特性图的横轴。相位GH GH 均为均为180180。 由上对应关系，极坐标图也可画成由上对应关系，极坐标图也可画成BodeBode图，如图图，如图5.4.15.4.1中中(a)(a)可画成可画成(c)(c)，(b)(b)可画成可画成(d)(d)。 20lg()()20lg10G jH jdB 为为NyquistNyquist轨迹与单位圆交点的频率，即对数幅轨迹与单位圆交点的频率，即对数幅频特性曲线与横轴交点的频率，亦即输入与输出频特性曲线与横轴交点的频率，亦即输入与输出幅值相等时的频率称

48、为幅值相等时的频率称为剪切频率剪切频率或或幅值穿越频率、幅值穿越频率、幅值交界频率幅值交界频率； 为为NyquistNyquist轨迹与负实轴交点的频率，亦即对数轨迹与负实轴交点的频率，亦即对数相频特性曲线与横轴交点的频率，称为相频特性曲线与横轴交点的频率，称为相位穿越相位穿越频率频率或或相位交界频率相位交界频率。 由图由图5.4.1 (b)5.4.1 (b)可见，可见， 曲线顺时针包曲线顺时针包围点（围点（1,j01,j0），即曲线先在），即曲线先在 时交于负实轴，时交于负实轴，后在后在 时才交于单位圆，亦即在时才交于单位圆，亦即在BodeBode图即图图即图5.4.1(d)5.4.1(d)

49、中，中，对数相频特性先在对数相频特性先在 时交于时交于180180线，对数幅频特性后线，对数幅频特性后 在时交于在时交于0 0分贝线分贝线。图图5.4.1(a)5.4.1(a)，图，图5.4.1(c)5.4.1(c)的情况则相反。的情况则相反。cg()()G jH jgcgc 如图如图5.4.2(a)5.4.2(a)所示，在所示，在a a点，相频特性由上而下点，相频特性由上而下穿过横轴，这称为穿过横轴，这称为负穿越负穿越；在在b b点，相频特性由下点，相频特性由下而上穿过横轴，这称为而上穿过横轴，这称为正穿越正穿越。 可以看出，可以看出，对数相频特性正穿越一次，就相当于对数相频特性正穿越一次，

50、就相当于NyquistNyquist轨迹由上而下穿过负实轴一次，此时相位轨迹由上而下穿过负实轴一次，此时相位减小（这里指绝对值减小）；反之，对数相频特减小（这里指绝对值减小）；反之，对数相频特性负穿越一次，就相当于性负穿越一次，就相当于NyquistNyquist轨迹由下而上穿轨迹由下而上穿过负实轴一次，此时相位增大过负实轴一次，此时相位增大。 由图由图5.4.2(a)5.4.2(a)可见，在可见，在0 0 范围内，对数相频范围内，对数相频特性正、负穿越次数之差为特性正、负穿越次数之差为0 0，那么在，那么在P P=0=0时，系时，系统稳定，此系统实际为一条件稳定系统。统稳定，此系统实际为一条

51、件稳定系统。 对对IIII型系统（如型系统（如 ），对其对数相频特性），对其对数相频特性一开始就由一开始就由180180向下，则算负半次穿越；反之，向下，则算负半次穿越；反之，若对数相频特性一开始就由若对数相频特性一开始就由180180向上，则算正向上，则算正半次穿越，如图半次穿越，如图5.4.35.4.3所示。所示。c21()ssa 根据根据NyquistNyquist判据和此种对应关系，对数判据可表述判据和此种对应关系，对数判据可表述如下：如下： 在在P P=0=0时时，若开环对数幅频特性比其对数相频特，若开环对数幅频特性比其对数相频特性先效于横轴，即性先效于横轴，即 ，如图，如图5.4.

52、1(c)5.4.1(c)所示，则所示，则闭环系统稳定；若开环对数幅频特性比其对数相频闭环系统稳定；若开环对数幅频特性比其对数相频特性后交于横轴，即特性后交于横轴，即 ，如图，如图5.4.1(d)5.4.1(d)所示，所示，则闭环系统不稳定；若则闭环系统不稳定；若 ，则闭环系统临界稳，则闭环系统临界稳定。或换言之：若开环对数幅频特性达到定。或换言之：若开环对数幅频特性达到0 0分贝，即分贝，即交于交于 时，其对数相频特性还在时，其对数相频特性还在180180线以上，即线以上，即相位还不足相位还不足180180，则闭环系统稳定；若开环相频，则闭环系统稳定；若开环相频特性达到特性达到180180时，

53、其对数幅频特性还在时，其对数幅频特性还在0 0分贝线分贝线以上，即幅值不足以上，即幅值不足1 1，则闭环系统不稳定。，则闭环系统不稳定。 cgcgcgc 一般系统的开环系统多为最小相位系统，即一般系统的开环系统多为最小相位系统，即P P=0=0，故可按上述条件来判别其稳定性。上述即为故可按上述条件来判别其稳定性。上述即为P P=0=0的的闭环系统稳定的充要条件。闭环系统稳定的充要条件。 若考虑包括若考虑包括P P00时的情况，对数判据则可全面地时的情况，对数判据则可全面地叙述如下叙述如下 在在BodeBode图上，当图上，当 由由0 0变到变到 时，开环对数相时，开环对数相频特性在频特性在0

54、0到到 的频率范围（即开环对数幅频特的频率范围（即开环对数幅频特性不为负值的范围）内，正穿越和负穿越性不为负值的范围）内，正穿越和负穿越180180轴线的次数之差为轴线的次数之差为P P/2/2时，闭环系统稳定；否则不时，闭环系统稳定；否则不稳定。稳定。 若开环对数幅频特性对横轴有多个剪切频率，如若开环对数幅频特性对横轴有多个剪切频率，如图图5.4.2(b)5.4.2(b)所示，则取剪切频率取大的所示，则取剪切频率取大的 判别，判别，因为若系统是稳定的，则用因为若系统是稳定的，则用 判别，自然也判别，自然也就是稳定的。就是稳定的。c3c12,cc 从从Nyquist稳定判据可推知：若稳定判据可

55、推知：若P=0的闭环系统稳的闭环系统稳定，且当定，且当Nyquist轨迹离点（轨迹离点（-1,j0）越远，则其）越远，则其闭环系统的稳定性越高；开环闭环系统的稳定性越高；开环Nyquist轨迹离点轨迹离点（-1,j0）越近，则其闭环系统的稳定性越低。）越近，则其闭环系统的稳定性越低。这便是通常所说的系统的相对稳定性，它通过这便是通常所说的系统的相对稳定性，它通过 对点（对点（-1,j0）的靠近程度来表征，其定量）的靠近程度来表征，其定量表示为表示为相位裕度相位裕度 和幅值裕度和幅值裕度Kg，如图，如图5.4.1所示。所示。()KGj5.5.1 5.5.1 相位裕度相位裕度 在在 为剪切频率为剪切频率 （ ）时，相频特性）时，相频特性GH GH 距距180180线的相位差值称为相位裕度。图线的相位差值称为相位裕度。图5.4.1(c)5.4.1(c)所示的系统不仅稳定，而且有相当的稳定性储备，所示的系统不仅稳定，而且有相当的稳定性储备，它可以在它可以在 的频率下，允许相位再增加的频率下，允许相位再增加 才达到才达到 的临界稳定条件，因此，相位裕度有时又叫做相的临界稳定条件，因此，相位裕度有时又叫做相位稳定性储备。位稳定性储备。 对于稳定系统，对于稳定系统， 必在必在BodeBode图横轴以上，这时称图横轴以上，这时称为正相位裕度，即有正的稳定性储备，如图为正相位裕度，即有正