中考数学：隐圆模型解题策略及答案详解

1、中考数学专题复习系列：让圆不再有隐形的翅膀“隐形圆”模型的解题策略【试题呈现】1 .如图，在ABC内有一点D,使得DA=DB=DC若/DAB=2（J,则/ACB=2 .（2016淮安）.如图，在RtABC中，/C=90,AC=6,BC=8,点F在边AC上，并且CF=2,点E为边BC上的动点，将CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是.第2题图第1页共7页3 .（2016安徽）如图，RtABC中，ABBC,AB=2,BC=3P是ABC内部的一个动点，且满足/PAB4PBC则线段CP长的最小值为.变式1.如图，在ABC中，/C=90,AC=BC=1,P为4ABC内一个动点

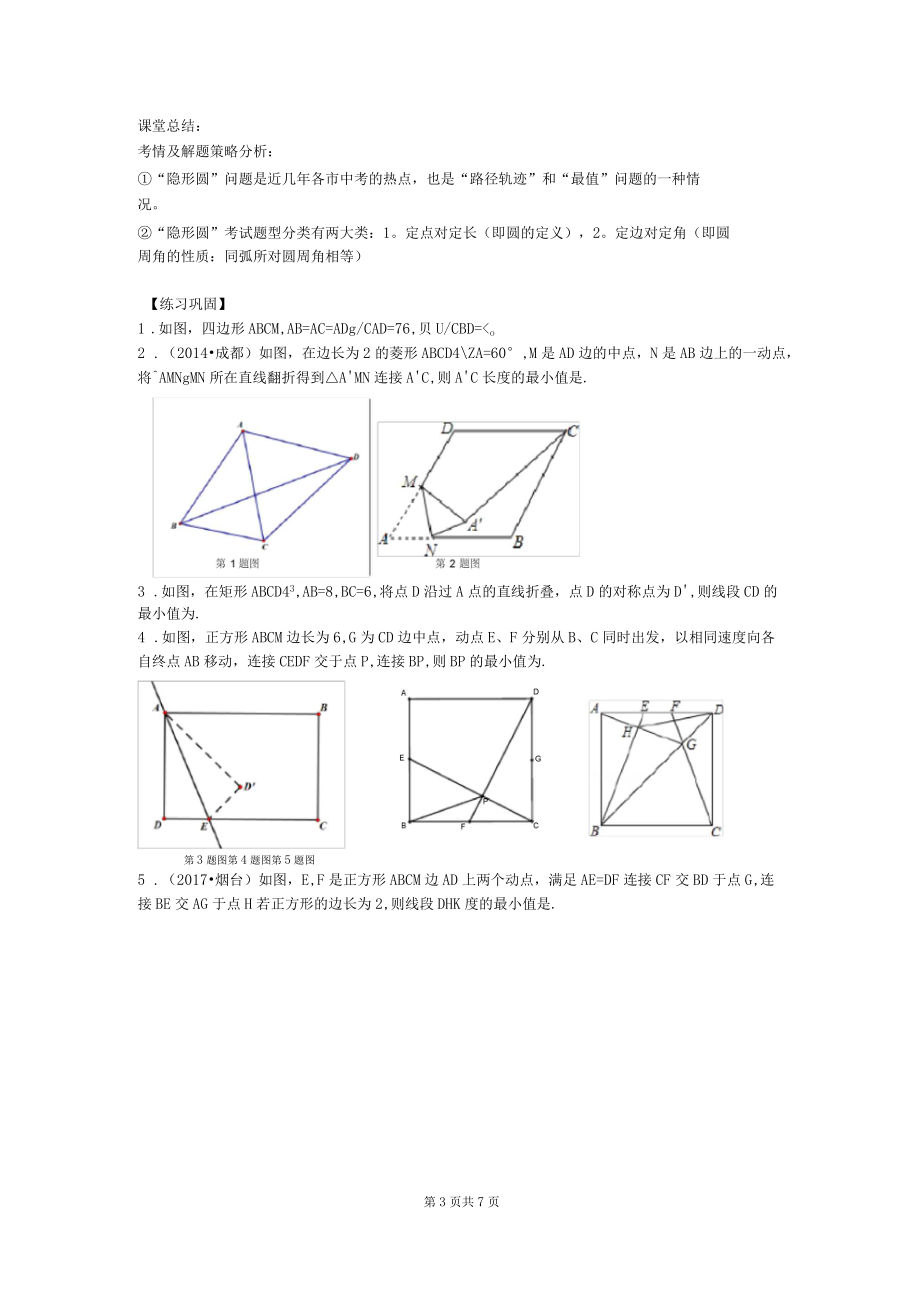
2、，满足/PAB=/PBC则线段CP长的最小值为变式2.如图，在ABC中，AC=BC=AB=2,斯ABC内一个动点，满足/PAB4PBC则线段CP长的最小值为第2页共7页课堂总结：考情及解题策略分析：“隐形圆”问题是近几年各市中考的热点，也是“路径轨迹”和“最值”问题的一种情况。“隐形圆”考试题型分类有两大类：1。定点对定长（即圆的定义），2。定边对定角（即圆周角的性质：同弧所对圆周角相等）【练习巩固】1 .如图，四边形ABCM,AB=AC=ADg/CAD=76,贝U/CBD=o2 .（2014成都）如图，在边长为2的菱形ABCD4ZA=60,M是AD边的中点，N是AB边上的一动点，将AMNgM

3、N所在直线翻折得到AMN连接AC,则AC长度的最小值是.3 .如图，在矩形ABCD43,AB=8,BC=6,将点D沿过A点的直线折叠，点D的对称点为D,则线段CD的最小值为.4 .如图，正方形ABCM边长为6,G为CD边中点，动点E、F分别从B、C同时出发，以相同速度向各自终点AB移动，连接CEDF交于点P,连接BP,则BP的最小值为.第3题图第4题图第5题图5 .（2017烟台）如图，E,F是正方形ABCM边AD上两个动点，满足AE=DF连接CF交BD于点G,连接BE交AG于点H若正方形的边长为2,则线段DHK度的最小值是.第3页共7页【拓展延伸】1.在ABC中,/ABC=90,AB=6,B

4、C=8,O为AC的中点,过O作O吐OF,OEOF分别交射线AB,BC于E、F,则EF的最小值为2.如图，已知A、B两点的坐标分别为（8,0）（0,-6）,C的坐标为（0,7）,点P是坐标平面内一个动点，且PC=5,线段PB与x轴交于点D,则ABD面积的最大值是第4页共7页参考答案详解【试题呈现】1.（定点对定长）分析：由DA=DB=DC得点D即为定点（圆心），DA,DB,DC为定长（半径）以点D为圆心，DA（或DAD。为半径作圆。一，1，可得/ACB/ADB（同弧所对圆周角是圆心角的一半）2DA=DB/DAB4DBA=20在？ABD中，/ADB=180-/DAB-/DBA=1401一7ACB-

5、ZADB=7CT22 .（定点对定长）分析：由折叠知FC=FP由CF=2可得，无论如何翻折，点F是定点（即为圆心），FC=F幅定长（即为半径）（始终抓CF=PF动点P到定点F的距离始终不变，）。以点F为圆心，FP（或FC）为半径作圆（无论点E如何运动，点P的运动轨迹在圆弧上运动）一点P到直线AB的最小值即转化为直线AB到圆的最小值问题。补充：直线到圆的最值模型过点F作FH，AB。（PH长即为点P到直线AB的最小值）由折叠知FC=FP=2贝UAF=AGFC=4,AB=1C由Rt?AFHRt?ABG得：AFFHABBG4FH1C8,FH3.2PHFHFP3.221.2，点P到直线AB的最小值为1.

6、23 .（定边对定角）解：PAB=/PBG/PBC吆ABP=9CPAB吆ABP=9C即/P=90（AB为定边，/P为定角，始终为90,）根据直径所对圆周角为直角，可得点P的运动轨迹以AB为直径的圆。CP的最小值即转化为“点到。O的最小值”问题。在Rt?OBG中,OGBG2OB2321210PG=OGOP=101CP长度的最小值是而1.第5页共7页补充：点到圆的最值模型参考答案：【练习巩固】1,1 .（定点对定长）以A为圆心，AB（或ACAD）为半径的圆，/CBD=/CAD=3822 .（定点对定长）如图：ME=2,CE=J3在Rt?MCE中，MCEC2ME2J、322.7.CA=MC-MA=J

7、7-1.AC长度的最小值是J7-1.3 .（定点对定长）此题点E为动点、点A为定点，由折叠知，始终有AD=AD。点D的运动轨迹是以点A为圆心，AD（或AD为半径的圆。CD最小值就转化为点C到。A的最小值。CD=AAD=1-6=44 .（定长对定角）动点E、F分别从BC同时出发，以相同速度相同BE=CF.?BCE?CDF.1./1=/2,/1+/3=90，/2+/3=90即/DPC=90（DC为定边，/DPC为定角，始终为90,）根据直径所对圆周角为直角，可得点P的运动轨迹以CD为直径的圆。BP的最小值即转化为“点B到。G的最小值”问题。BP=BG-PG3.5-35 .（定边对定角）同第2题，通过导角得到/AHB=90.根据直径所对圆周角为直角，可得点H的运动轨迹以AB为直径的圆。第6页共7页由？ADG?CDG可得/1=Z2由？ABE?DCF可得/2=Z3/1=Z31+Z4=90