第一章 轴向拉伸及压缩

1、F1-1 工程实际中的轴向拉伸和压缩问题工程实际中的轴向拉伸和压缩问题F1-2 拉伸和压缩时的内力拉伸和压缩时的内力F1-3 截面上的应力截面上的应力F1-4 拉伸和压缩时的变形拉伸和压缩时的变形F1-5 拉伸和压缩时材料的力学性能拉伸和压缩时材料的力学性能F1-6 拉伸和压缩时的强度计算拉伸和压缩时的强度计算F1-7 拉伸和压缩超静定问题拉伸和压缩超静定问题F1-8 应力集中的概念应力集中的概念F1-9 变形能的概念变形能的概念拉伸或压缩杆件大多数是等截面直杆等截面直杆，其特点是： w在杆两端受一对大小相等、方向相反的力，力的作用线与杆的轴线重合，若两端的两个力向外，则是拉伸，向内则是压缩；

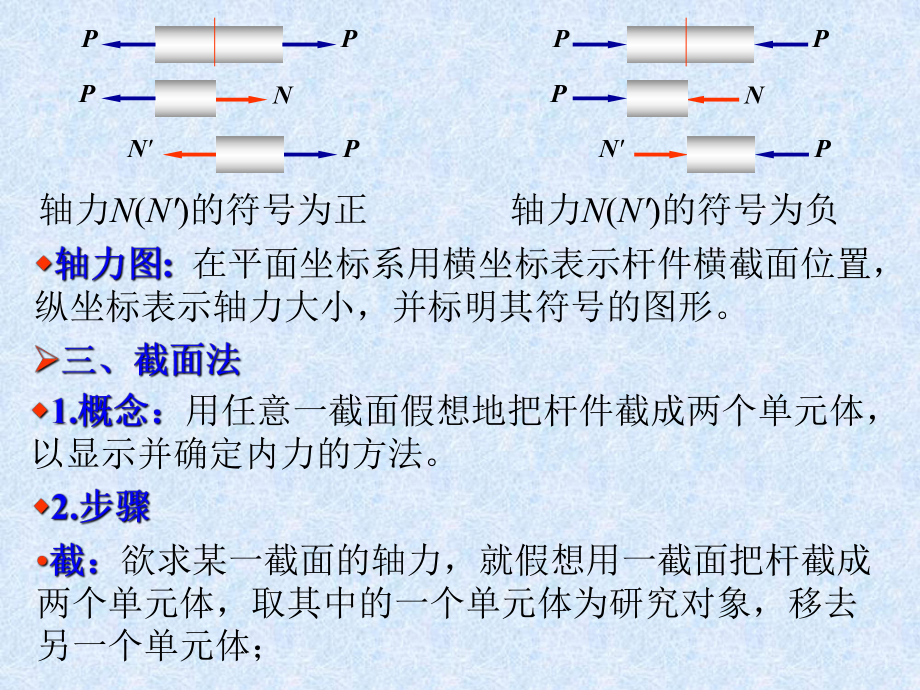
2、 w有一些杆受到两个以上的轴向外力作用，仍属于拉压杆。 杆件沿轴线方向伸长或缩短。 所研究物体内部一部分对另一部分之间的作用力。 物体内部：方向相反：大小相等：成对出现： 作用线与杆件轴线重合的内力。轴力背离截面时称为轴向拉力，规定为正值，指向截面时称为轴向压力，规定为负值。同一截面两侧的轴力大小相等，符号相同。 NNPPPP轴力N(N)的符号为正NNPPPP轴力N(N)的符号为负 在平面坐标系用横坐标表示杆件横截面位置，纵坐标表示轴力大小，并标明其符号的图形。 用任意一截面假想地把杆件截成两个单元体，以显示并确定内力的方法。 欲求某一截面的轴力，就假想用一截面把杆截成两个单元体，取其中的一个

3、单元体为研究对象，移去另一个单元体； 用轴力代替移去单元体对保留单元体的作用，一般假定其符号为正(即拉向轴力)； 建立平衡方程，由已知外力确定未知轴力。 【例1-1】求杆的轴力并画出轴力图 NABAPA=PAPA=PBPB=2PCPC=4PDPD=2PEPE=P【解】1)根据载荷“突变”情况，采用截面法从左至右分段列平衡方程求各段的轴力: AB段: 0NPFABAixBC段: 0NPPFBCBAixNBCAPA=PBPB=2PPPNAABPPPNBABC3)(APA=PBPB=2PCPC=4PDPD=2PEPE=P0NPPPFCDCBAixCD段: DE段: 0NPPPPFDEDCBAixAP

4、A=PBPB=2PCPC=4PNCDPPPPNCBACD)()(PPPPPNDCBADE)()()(APA=PBPB=2PCPC=4PDPD=2PNDE2)画轴力图: ABCDE+单元体上背离截面的外力在截面上产生正的轴力，指向截面的外力在截面上产生负的轴力;轴力的大小等于外力的大小;截面上总的轴力等于单元体上的所有外力单独作用产生的轴力的代数和。P3PPPANTP p内力在截面上的密集程度称为应力应力。即： dAdPAPpA0lim将P沿截面分解成法向内力N和切向内力T 。dAdNANA0lim称为正应力正应力，它垂直于截面，并规定拉应力为正值，压应力为负值。 dAdTATA0lim称为剪应

5、力剪应力，并规定使单元体绕其上任一点顺时针转的为正，反之为负。 +-+-PP国际单位为帕斯卡，简称帕，用表示Pa。其常用单位有兆帕(MPa)、吉帕(GPa)等。mN1P12aP10kP10MP10PG1a9a6a3a取等截面直杆作拉伸实验。 拉伸前拉伸前: : ab、cd为直线且均垂直于轴线 。abcdabcd拉伸后拉伸后: :ab、cd仍为直线且均垂直于轴线， ab 与cd 间距离变大，杆变细。 1)变形前的横截面，变形后仍保持为垂直于杆轴的平面，即平面假设平面假设。 2)任意两横截面间纵向纤维伸长量(或缩短量)是相等的，即应力是均布的。故： ANPPabcdPl1d1ldP 绝对变形001

6、1dddlllPP 绝对变形0011dddlllll纵向线应变，无量纲，拉伸为正，压缩为负。 dd横向线应变，无量纲，拉伸为负，压缩为正。ldl1d1当拉压杆件的应力不超过材料比例极限时，横向线应变与纵向线应变之比为一常数，其绝对值称为泊松比泊松比，用表示。 即： |或 E即：构件的应力未超过材料的比例极限时，其应力与应变成正比。 E材料的弹性模量弹性模量，与应力量纲相同。 w虎克定律的另一表达式EANll EA构件的抗拉抗拉( (压压) )刚度刚度w若构件在第i段标距li内Ei、Ai、Ni为常数，则变形为niiiiiAElNl1xtAtEdttNx0)()()()(w若构件E(x)、A (x

7、) 、N (x)为截面位置x的连续函数，则变形为：这里仅研究材料在常温静载常温静载下的机械性质。 试样中段用于测量拉伸变形的部分。 对圆截面试样要求其标距满足l0=10d0 或 l0=5d0 。 l0d0ABPfO特征：特征：在OAB段任何处御除载荷后，曲线能沿原路返回。其中OA段为一直线，即应力与应变成正比，比例系数为弹性模量E，且E为直线OA的斜率；与A点对应的应力称为比例极限比例极限，即是材料应力与应变成正比的最大应力。 应力超过比例极限时，应力与应变不再成正比关系即AB段是微弯曲线。B点对应的应力称为弹性极限弹性极限。 CDs特征：特征：在过B点至试样断裂的整个过程的任何地方卸除载荷后

8、曲线均不能沿原路返回，只能沿与OA平行的直线返回。试样表面将出现与轴线成45左右的滑痕，材料发生永久变形称为塑性应变塑性应变。如果此时再加载，曲线将沿与OA平行的直线上升至原卸载点。 过B点后变形增加较快而应力增加不显著，对应于C点的应力称为上屈服点上屈服点。过C点后不计初始瞬时效应时的最低点D称为下屈服点下屈服点。从D点后曲线上将出现近乎水平的微小波动段。一般取D点对应的应力为屈服极限屈服极限。 ABPfOE特征：特征：与弹性阶段相比，应力增加缓慢，变形增加较快，变形大部分属于塑性变形，曲线最高点G对应的应力称为强度极限强度极限。如果此时卸载，曲线将沿FO1下降，再加载，曲线将沿O1F上升，

9、比例极限和塑性极限都将增大，该过程称为冷作硬化冷作硬化。冷作硬化现象经退火后可消除。 FGbO1EABCDPfsOABCDFEGPf sO1bOHO2特征：特征：过G点后，变形集中在试样的薄弱地方，横向尺寸急剧缩小，出现“颈缩”现象，虽然曲线下降但由于横截面尺寸较名义值变小，实验证明颈缩截面上的实际应力却是一直在增加，最后沿横截面断裂。 此时的残余应变OO2()称为延伸率延伸率。延伸率与截面收缩率反映材料塑性性能指标。 %100001lllnl0试件原来的标距段长度。 l1试件拉断的标距段长度。 n试样标距直径比。 00010100AAAA0试件原来横截面积。 A1试件断裂后断口处的横截面积。

10、 一般称5的材料为塑性材料塑性材料，如低合金钢、碳素钢、青铜等；1安全因数安全因数 对塑性材料：nss 对脆性材料：nbbns、nb分别为按屈服极限和强度极限规定的安全因数，一般地nsnb。 确定安全系数一般应考虑的因素: 材料的均匀程度； 载荷估计的准确性； 计算方法方面的简化和近似程度；构件加工工艺，构件工作条件；构件的重要性。 一般在常温静载情况下，塑性材料的安全系数ns=1.52.0，脆性材料安全系数nb=2.53.0。 AN杆件横截面上的工作应力； N横截面上的轴力； A横截面面积； 材料的许用应力。 AN最大工作应力是否超过材料的许用应力。NA AN 【例例1-2】图示等厚度直杆，

11、BC段加工有一槽。已知：弹性模量 E = 200 GPa，许用应力=220MPa，l=200。尺寸单位为mm，力的单位为kN。1)作该杆的轴力图；2)计算伸长量lAE；3)校核杆的强度。 【解】1)根据杆上的载荷“突变”情况分段画轴力图： 20 kN10 kNCDEAB+10102010llllABCD103020E2)计算伸长量lAE )(DEDECDCDBCBCABABDECDBCABAEANANANANEllllll3)校核强度 MPa100102010203ABABABANMPa200101010203BCBCBCANMPa50102010103CDCDCDANMPa100101010

12、103DEDEDEAN因 MPa200|)| |,| |,| |,max(|DECDBCAB故该杆安全。 mm 15. 0)10101010102010101010102010201020(1020020033333【例1-3】图示结构中，圆杆AB直径dAB=30mm，许用应力AB=120MPa，圆杆BC直径dBC=20mm，许用应力BC=160MPa，不考虑结构自重。(1)求其所能承受的最大载荷W？(2)若载荷的最大值W=100kN，求两杆的最小直径。 【解】1)设AB杆、BC杆的内力如图示。060sin060cosWNFNNFABiyABBCixABC60WNBC60WNAB2)AB杆、B

13、C杆能承受的最大载荷： 382ABABABABABdWAN342BCBCBCBCBCdWAN360cot3260sinWWNWWNBCABkN5 .73832ABABdWkN1 .87432BCBCdW故最大载荷为73.5kN。 3)AB杆、BC杆的最小直径： mm351012031010083838632ABABABABABABABWddWANmm4 .211016031010043434632BCBCBCBCBCBCBCWddWAN【例1-4】 图示蒸气机气缸内径D=560mm，蒸汽压力p=2.5MPa，活塞杆直径d=100mm，许用应力=76MPa。气缸和缸盖用螺栓连接，螺栓内径d1=3

14、0mm，许用应力t=60MPa。校核活塞杆强度并计算缸盖所需螺栓个数n。 Dppd1d【解】1)校核活塞杆强度 DdppNkN596105 . 210)100560(4)(40662222pdDPNPNFix活塞杆的工作应力为： MPa9 .75Pa10100105964623AN2)计算螺栓个数n 螺栓在工作中受拉伸，总拉力等于气缸盖所受的总推力P，则每个螺栓的轴力 。nPN11410601030105964466232111111tttdPAPnnAPAN由螺栓的强度条件得：ppd1dDN1【例1-5】图示均质正圆锥台密度为，高为h，上、下底面直径分别为d、D。写出其在自重作用下的轴力、应

15、力和变形公式。xdxhdxN(x)N(x)+d N(x)【解】取单元体作受力分析0)()()()(xdNxNdxxAgxNFiydxxgAxdN)()(dxxAg)(dhdDxhxAx)(4)(2横截面面积因)()(12)()(334hdhddDxhhdDgxN故)()()(3)()()()(232hddDxhhdhddDxhhdDgxAxNx故hxdxxAgxN)()(dxxddxxxdxx)()()()()(设x横截面变形为(x)，(x+dx)横截面变形为: (x)+ d(x)由线应变的定义得：由虎克定律得：Exdxxdx)()()(Edxxxd)()(xdxhddDxhhdhddDxhh

16、EdDgx0232)()()(3)()()(12)()(12)(3)(222hddDxhhddDxhhddDhhddDhhEgx故dx(x)(x)+ d(x) 能用静力平衡方程完全求解的问题。 未知力个数多于独立的静力平衡方程数目，仅仅根据平衡方程尚不能全部求解的问题。 未知力个数与独立方程个数之差。该差为一则为一次超静定，为二则为二次超静定等。 静力学平衡方程； 变形与内力等的关系； 指保持结构连续的变形几何条件。这是重点和难点。 【例1-6】图示结构中杆1和杆2的抗拉刚度为E1A1，杆3的抗拉刚度为E3A3 ，求各杆件的内力。 【解解】1)以节点O为研究对象。 cos20cos21331N

17、PNPNNFiy2)物理方程。 AElNl11111AElNl333333)变形协调方程。cos31ll4)求解。 cos2cos311332111AEAEAPENcos231133333AEAEAPENl3123OPl1POllllcos 由所求结果知：超静定问题中杆件内力(或构件约束反力)不仅与载荷有关，还与杆件的抗拉(压)刚度有关。【例1-7】已知杆AB、AC、DE的长度为LAB、LAC、LDE， 杆AB、AC的抗拉刚度为EABAAB、EACAAC。求杆AB、AC的内力。 A【解解】1)静力平衡方程。0cossincossin)(LPLNLNmDEACACABABiDFNABPECBDF

18、DxFDy2)物理方程。AELNLABABABABAB3)变形协调方程。LLLLACABACABcoscossinsinAELNLACACACACAC4)解方程得： 2sin2sin2sin222LAELAELAPENACACACABABABDEABABAB2sin2sin2sin222LAELAELAPENACACACABABABDEACACACDBCEBCEALLCCBBLLACABACABsinsincoscosNAC在超静定结构中，构件由于制造的几何误差，装配成结构后虽然未承受外载荷，但在各构件中也存在内力。这种内力引起的应力称装配应力装配应力。 计算装配应力的关键在于根据变形协调条件

19、建立变形几何方程。 【例1-8】图示结构中杆1和杆2的抗拉刚度为E1A1 ，杆3的抗拉刚度为E3A3 ，制造误差为。求各杆装配内力。 O13O0O2l1l3【解解】1)以节点O为研究对象，建立方程： cos20cos21313NNNNFiy2)物理方程。AElNl11111AElNl333333)变形协调方程。ll13cos)(4)求解。 cos2cos311133133111AElAElAEAENcos2cos23111331233113AElAElAEAEN【思考【思考】装配好后若在O点垂直向下作用一力P，该如何求各杆件的内力？【答【答】令平衡方程右边等于P即可。O13O0O2l1l3在超

20、静定结构中，构件的长度互相牵制，不能自由收缩，因此温度变化将导致各构件的长度的变化，使得构件产生内力，这种内力称为温度内力温度内力。由温度内力引起的应力称为温度应力温度应力。 计算温度应力的关键在于根据变形协调条件建立变形几何方程和写出正确的物理方程。 【例1-9】图示结构中杆1和杆2的抗拉刚度为E1A1 ，线膨胀系数为1= 2 ，杆3的抗拉刚度为E3A3 ，线膨胀系数为3 。设升温为T，求各杆的温度内力。 l3123Ol1O【解解】1)以节点O为研究对象，建立静力平衡方程： cos20cos21313NNNNFiyl3123Ol1O2)物理方程。设二力杆1、杆2受压，杆3受拉，则变形满足：

21、AElNTll1111111由温度升高和压缩内力引起的变形 AElNTll3333333由温度升高和拉伸内力引起的变形 3)变形协调方程。 cos31ll4)求解。cos2)cos(3113323133111AEAETAEAENcos2cos)cos(23113323133113AEAETAEAEN杆1、杆2受压，杆3受拉的假定成立与否由 的符号确定。 cos231【思考】【思考】若在O点垂直向下作用一力P，该如何求各杆件的内力？【答】【答】令平衡方程右边等于P即可。【思考【思考】如果上述结构同时存在装配误差、温度变化、外载荷，如何求解？ 【解】【解】1)静力平衡方程： 0cos231PNNFiy2