matlab酵母培养物的离散阻滞增长模型

1、辽宁工程技术大学上机实验报告实验名称酵母培养物的离散阻滞增长模型院系理学院专业理科实验班级姓名学号日期2015.4.20实验目的简述本次实验目的：掌握酵母培养物的阻滞增长差分方程模型的分析与建模方法，并会利用Matlab作数值计算与误差分析.实验准备你为本次实验做了哪些准备：上课听讲，下课复习课本，不明白之处查阅资料。实验进度本次共启1个练习，完成1个。实验总结本次实验的收获、体会、经验、问题和教训：教师评语具体处理过程和相应实验结果:已知从测量酵母培养物增长的实验收集的数据如表:/h0123456789生物量/g9.618.329.047.271.1119.174.6257.350.441.

2、1370时刻/h101112131415161718生物量/g513.559.594.629.4640.8651.655.9659.661.378168实验要求：1、作图分析酵母培养物的增长数据、增长率、与相对增长率.2、建立酵母培养物的增长模型.3、利用线性拟合估计模型参数，并进行模型检验，展示模型拟合与预测效果图4、利用非线性拟合估计模型参数，并进行模型检验，展示模型拟合与预测效果图5、请分析两个模型的区别，作出模型的评价.实验内容：1、作图分析酵母培养物的增长数据、增长率、与相对增长率.(1)增长数据：绘制x关于k的散点图：x=9.6,18.3,29.0,47.2,71.1,119.1,

3、174.6,257.3,350.7,441.0,513.3,559.7,594.8,629.4,640.8,651.1,655.9,659.6,661.8;k=0:1:18;plot(k,x,'k+')xlabel('时间k(小时)')ylabel('生物量x(克)')title('x关于k的散点图')x关于k的散点图700,1F,1-1F,4600+-4500-4-)+克400rrx(+S300-生4200-r+100，一-+440-1-11111111024681012141618时间k(小时)即x关于k的散点沿s型曲线分布，

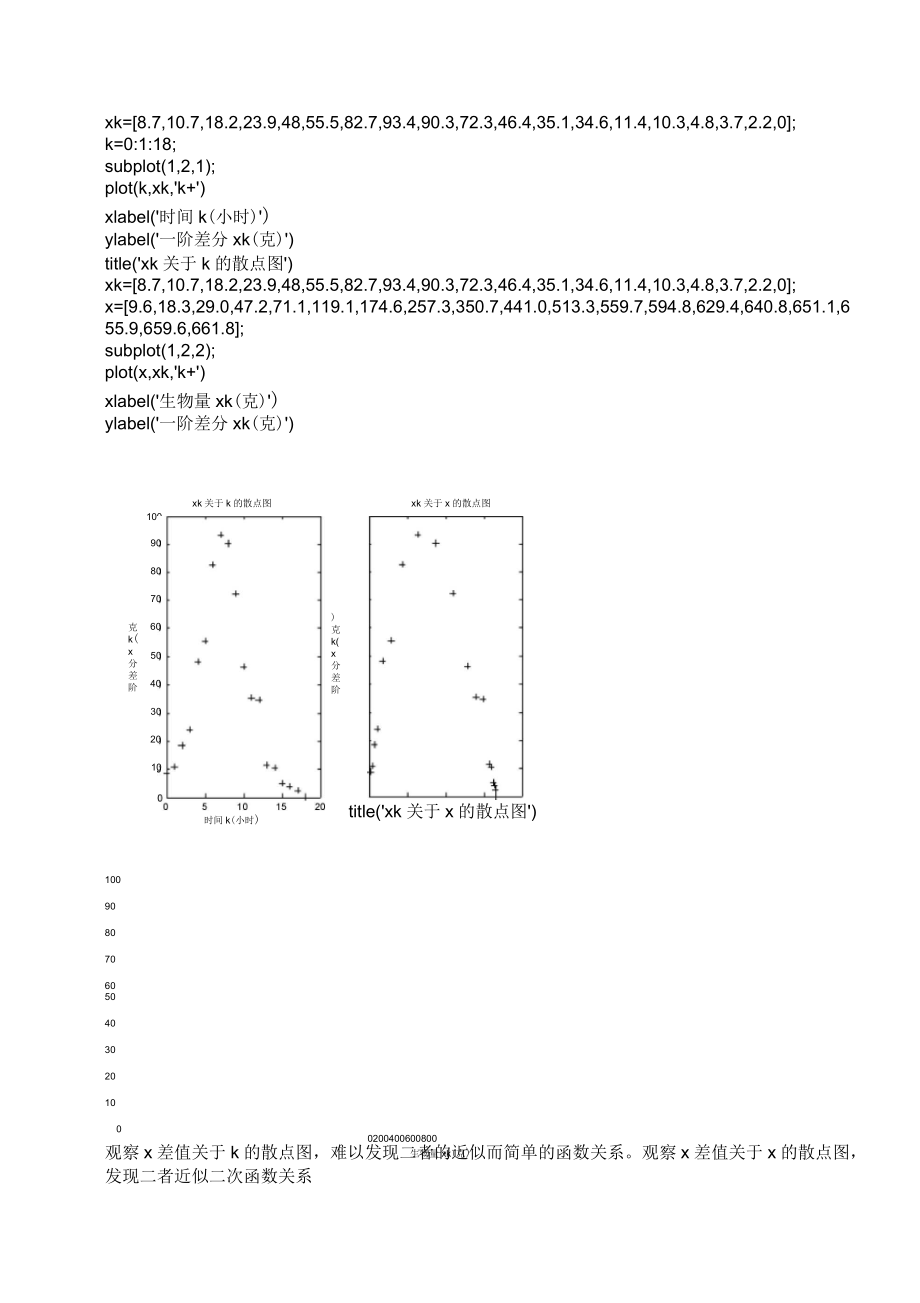
4、x随着k单调增加，x可能趋于稳定值，极限可能存在(2)增长率：绘制x差值关于k的散点图以及绘制x差值关于x的散点图:xk=8.7,10.7,18.2,23.9,48,55.5,82.7,93.4,90.3,72.3,46.4,35.1,34.6,11.4,10.3,4.8,3.7,2.2,0;k=0:1:18;subplot(1,2,1);plot(k,xk,'k+')xlabel('时间k(小时)')ylabel('一阶差分xk(克)')title('xk关于k的散点图')xk=8.7,10.7,18.2,23.9,48,55.

5、5,82.7,93.4,90.3,72.3,46.4,35.1,34.6,11.4,10.3,4.8,3.7,2.2,0;x=9.6,18.3,29.0,47.2,71.1,119.1,174.6,257.3,350.7,441.0,513.3,559.7,594.8,629.4,640.8,651.1,655.9,659.6,661.8;subplot(1,2,2);plot(x,xk,'k+')xlabel('生物量xk(克)')ylabel('一阶差分xk(克)')100克k(x分差阶xk关于k的散点图908070605040302010时

6、间k(小时)克k(x分差阶xk关于x的散点图title('xk关于x的散点图')1009080706050403020100200400600800生物量xk(克)0观察x差值关于k的散点图，难以发现二者的近似而简单的函数关系。观察x差值关于x的散点图，发现二者近似二次函数关系xk=-a1*xkA2+a2*xk;,实质就是离散阻滞增长模型。(3)相对增长率：绘制rk差值关于k的散点图以及绘制rk关于xk的散点图:rk=0.90625,0.5847,0.62759,0.50636,0.67511,0.46599,0.47365,0.363,0.25749,0.16395,0.09

7、0395,0.62712,0.058171,0.018112,0.016074,0.0073721,0.0056411,0.0033354,0;k=0:1:18;subplot(1,2,1);plot(k,rk,'k+')xlabel('时间k(小时)')ylabel('增长率rk(%)')title('rk关于k的散点图')rk=0.90625,0.5847,0.62759,0.50636,0.67511,0.46599,0.47365,0.363,0.25749,0.16395,0.090395,0.62712,0.05817

8、1,0.018112,0.016074,0.0073721,0.0056411,0.0033354,0;x=9.6,18.3,29.0,47.2,71.1,119.1,174.6,257.3,350.7,441.0,513.3,559.7,594.8,629.4,640.8,651.1,655.9,659.6,661.8;subplot(1,2,2);plot(x,rk,'k+')xlabel('生物量xk(克)')ylabel('增长率rk(%)')title('rk关于x的散点图')0.21+0.1+-+。1105101520

9、时间k(小时)rk关于k的散点图10.9个rk关于x的散点图1r1r-0.20.1200400600800生物量xk(克)876000%/率长增0.94观察rk关于k的散点图，难以发现二者的近似而简单的函数关系。观察rk关于xk的散点图，发现二者近似线性递减关系rk=r*(1-xk/N);由rk=(x(k+1)-x(k)/x(k),代入上式，建立离散阻滞增长模型。2、建立酵母培养物的增长模型.在营养有限的环境下，假设用前差公式计算的增长率rk随着生物量xk的增加而线性递减，即rk=rk=(x(k+1)-x(k)/x(k)=r*(1-x(k)/N),k=0,1,2根据模型假设，即可建立离散阻滞增

10、长模型x(k+1)=x(k)+r*x(k)*(1-x(k)/N),k=0,1,2,3、利用线性拟合估计模型参数，并进行模型检验，展示模型拟合与预测效果图首先，根据rk和xk的数据拟合出r(k)=r*(1-x(k)/N)的参数r和N,拟合效果图如1.(3)-1图所示。然后根据观测数据直接取x0=9.6,用循环语句按照x(k+1)=x(k)+r*x(k)*(1-x(k)/N),k=0,1,2,进行迭代计算，算出第018小时酵母生物量的模拟值，并计算误差平方和，绘制模拟效果图和模拟误差图。用matlab编程如下：t=0:18;x=9.6,18.3,29.0,47.2,71.1,119.1,174.6

11、,257.3,350.7,441.0,513.3,559.7,594.8,629.4,640.8,651.1,655.9,659.6,661.8;r=(x(2:19)-x(1:18)./x(1:18);a1=polyfit(x(1:18),r,1);r1=a1(2),N1=-a1(2)/a1(1)x1=x；fork=1:18x1(k+1)=x1(k)+r1*x1(k)*(1-x1(k)/N1);endresd1=x-x1;sse1=sum(resd1.A2)subplot(2,1,1),plot(t,x,'k*',t,x1,ks,)axis(-1,19,0,670),legen

12、d(观测值','模拟值',4)xlabel('时间k(小时),),ylabel('生物量x_k(克)')title(,(1)离散阻滞增长模型的模拟效果图，线性拟合,)subplot(2,1,2),plot(t,resd1,'k.',-1,19,0,0,'k')axis(-1,19,-40,40),legend('观测值','模拟值',4)xlabel('时间k(小时),),ylabel('模拟误差')title('(2)离散阻滞增长模型的模拟误差，线性

13、拟合,)结果：r1=0.6693N1=635.7055sse1=6.2932e+03(1)离散阻滞增长模型的模拟效果图，线性拟合克kx量物生6004002000'r'口0由由古古丁古口印斗观测值田田口模拟值由用田bIIIIYII024681012141618时间k(小时)差误拟模(2)离散阻滞增长模型的模拟误差，线性拟合4、利用非线性拟合估计模型参数，并进行模型检验，展示模型拟合与预测效果图用matlab编程如下：函数文件fun_3_4_2.m：functiony=fun_3_4_2(b,x)y=zeros(size(x);y(1)=b(3);fork=2:length(x)y

14、(k)=y(k-1)+b(1).*y(k-1)*(1-y(k-1)./b(2);end脚本：t=0:18;x=9.6,18.3,29.0,47.2,71.1,119.1,174.6,257.3,350.7,441.0,513.3,559.7,594.8,629.4,640.8,651.1,655.9,659.6,661.8;a2,resd2=nlinfit(t,x,fun_3_4_2,0.5,660,9.6)sse=sum(resd2.A2)subplot(2,1,1)plot(t,x,'k*',t,fun_3_4_2(a2,t),'ks')axis(-1,19

15、,0,670)legend(观测值','模拟值',4)xlabel('时间k(小时),ylabel('生物量x_k(克)')title('(1)离散阻滞增长模型的模拟效果以，非线性拟合')subplot(2,1,2)plot(t,resd2,'k.',-1,19,0,0,'k')axis(-1,19,-40,40)xlabel('时间k(小时),ylabel('模拟误差')title('(2)离散阻滞增长模型的模拟误差，非线性拟合')结果如下:a2=0.5604652.463414.9997resd2=-5.39975.134111.84062.48075.1393-4.9118-6.756210.87271.03847.88769.6673-7.4948-11.6748-14.2442-17.8488-4.1746-4.7021-4.1982-3.0640sse=1.3535e+03(1)离散阻滞增长模型的模拟效果图，非线性拟合克kx量物生600400200040困a曲曲国步观测值囚m值口模拟值ooO22-差误拟模-40024681012141618时间k（小时）024681012141618时间k(小时)(2)离散阻滞