瞬时变化率导数_第1页
瞬时变化率导数_第2页
瞬时变化率导数_第3页
瞬时变化率导数_第4页
瞬时变化率导数_第5页
已阅读5页，还剩9页未读， 继续免费阅读

下载本文档

版权说明：本文档由用户提供并上传，收益归属内容提供方，若内容存在侵权，请进行举报或认领

文档简介

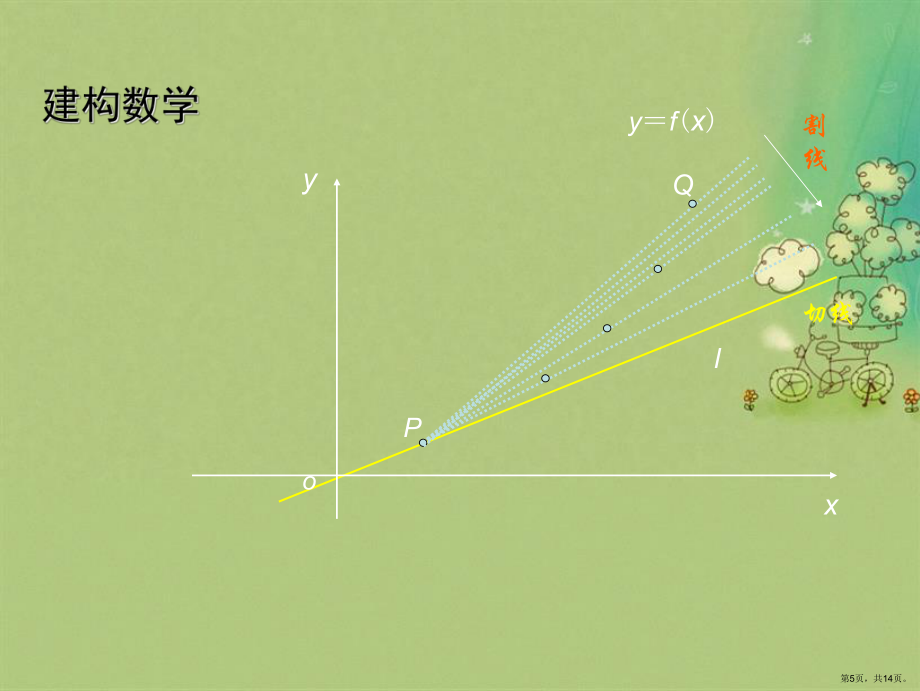
1、瞬时变化率导数第1页，共14页。放大放大第2页，共14页。从上面的图形变化过程来看：第3页，共14页。l1Ol2Pl1，l2问题一：试判断哪一条直线在点P附近更加逼近曲线；问题二：在点P附近能作出一条比l1 ， l2更加逼近曲线的直线l3吗？问题三：在点P附近还能作出比l1，l2 ，l3更加逼近曲线的直线吗？第4页，共14页。PQoxy割线切线lyf(x)第5页，共14页。 如图，设Q为曲线C上不同于P的一点，直线PQ称为曲线的割线. P为已知曲线C上的一点，如何求出点P处的切线方程？随着点Q沿曲线C向点P运动，割线PQ在点P附近逼近曲线C，当直线l，这条直线l也称为曲线在点P处的切线这种方法

2、叫割线逼近切线.点Q无限逼近点P时，直线PQ最终就成为经过点P处最逼近曲线的yOxPQ第6页，共14页。试求f (x)=x2在点(2,4)处的切线斜率Qx分析：设P(2，4)，Q(xQ，f(xQ)2()44222QQPQQQQf xxkxxx则割线PQ的斜率为 当Q沿曲线逼近点P时，割线PQ逼近点P处的切线，从而割线斜率逼近切线斜率； 当Q点横坐标无限趋近于P点横坐标时，即xQ无限趋近于2时，kPQ无限趋近于常数4 从而曲线f(x)x2在点(2，4)处的切线斜率为4第7页，共14页。22(2)444Pxkxxxxx Q2422QPQQQxkxx2Qxx 令，练习：试求f (x)x21在x1处的

3、切线斜率2Qxx所以 解：设P(2，4)，Q(xQ，xQ2)，则割线PQ的斜率为： 当xQ无限趋近于2时，kPQ无限趋近于常数4，从而曲线f(x)x2在点(2，4)处的切线斜率为4解：设P(2，4)，Q(2x，(2x)2)，则割线PQ的斜率为： 当x无限趋近于0时，kPQ无限趋近于常数4，从而曲线f(x)x2在点(2，4)处的切线斜率为4第8页，共14页。2(1)1222PQxkxxxxx2 练习：试求f (x)x21在x=1处的切线斜率 当割线逼近切线，割线斜率逼近切线斜率Q解：由题意，设P(1，2)，Q(1x，(1x)21)，则割线PQ斜率为 当x无限趋近于0时，kPQ无限趋近于常数2，从

4、而曲线f(x)x21在点x1处的切线斜率为2第9页，共14页。yxOy = f(x)xx0X0 xPQf (x0+x) f (x0)切线割线x2.求出割线PQ的斜率 ，并化简. 求曲线y=f (x)上一点P(x0,f(x0)处切线斜率的一般步骤：3. 令x 趋向于0，若上式中的割线斜率“逼近”一个常数， 则其即为所求切线斜率1.设曲线上另一点Q(x0+x,f(x0 + x)（即 y)()00()PQf xxf xkx第10页，共14页。变式训练： 第11页，共14页。课堂练习：第12页，共14页。练习：第13页，共14页。割线PQP点处的切线Q无限逼近P时割线PQ的斜率P点处的切线斜率 Q无限逼近P时Q无限逼近P时即区间长度

人人文库> 全部分类> 教育资料 > 课件下载

温馨提示

  • 1. 本站所有资源如无特殊说明，都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
  • 2. 本站的文档不包含任何第三方提供的附件图纸等，如果需要附件，请联系上传者。文件的所有权益归上传用户所有。
  • 3. 本站RAR压缩包中若带图纸，网页内容里面会有图纸预览，若没有图纸预览就没有图纸。
  • 4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
  • 5. 人人文库网仅提供信息存储空间，仅对用户上传内容的表现方式做保护处理，对用户上传分享的文档内容本身不做任何修改或编辑，并不能对任何下载内容负责。
  • 6. 下载文件中如有侵权或不适当内容，请与我们联系，我们立即纠正。
  • 7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

最新文档

评论

0/150

提交评论