概率论与随机过程：第3章 第四节 条件分布

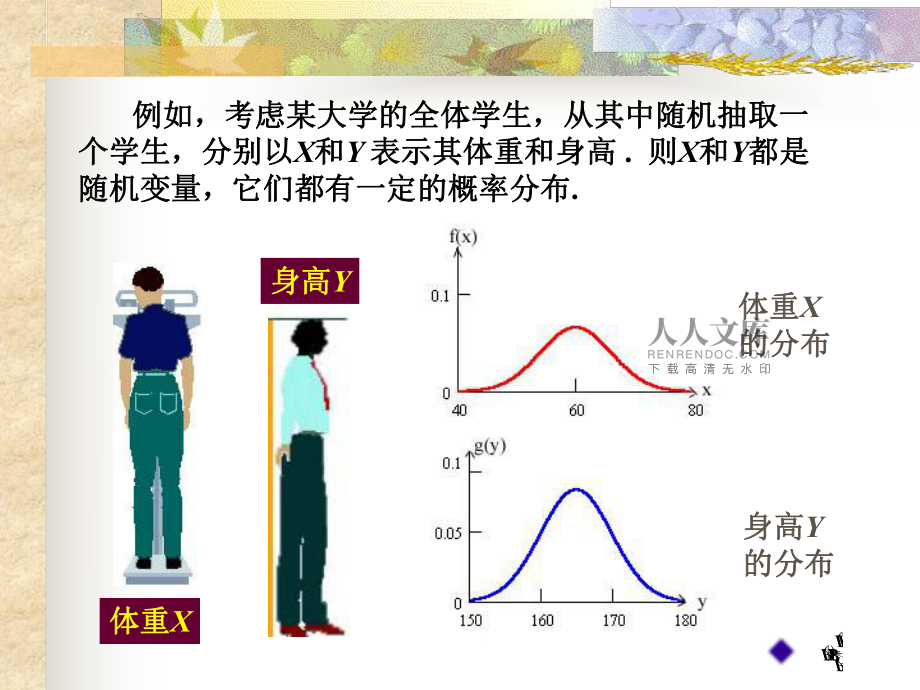
1、) () () | (BPABPBAP第四节 条件分布 在第一章中，我们介绍了条件概率的概念在第一章中，我们介绍了条件概率的概念 .在事件在事件B发生发生的条件下事件的条件下事件A发生的条件概率发生的条件概率)()()|(BPABPBAP推广到随机变量推广到随机变量 设有两个设有两个r.v X,Y ， 在给定在给定Y取某个或某些值的取某个或某些值的条件下，求条件下，求X的概率分布的概率分布.这个分布就是条件分布这个分布就是条件分布.) () () | (BPABPBAP 例如，考虑某大学的全体学生，从其中随机抽取一例如，考虑某大学的全体学生，从其中随机抽取一个学生，分别以个学生，分别以X和和Y

2、 表示其体重和身高表示其体重和身高 . 则则X和和Y都是都是随机变量，它们都有一定的概率分布随机变量，它们都有一定的概率分布.体重体重X身高身高Y体重体重X的分布的分布身高身高Y的分布的分布) () () | (BPABPBAP 现在若限制现在若限制1.7Y0,pj0，考虑在事件Y=yj已发生的条件下事件X=xi发生的概率,即 X=xi|Y=yj, i=1,2,.的概率,由条件概率公式, ., 2 , 1,| ippyYPyYxXPyYxXPjijjjiji) () () | (BPABPBAP 显然，上述条件概率具有分布律的特性(1).P PX=xi|Y=yj0； 1|).2(11 jjij

3、ijijippppyYxXP1定义 设(X,Y)是二维离散型随机变量,对于固定 的j，若PY=yj0，则称 .2 , 1,| ippyYPyYxXPyYxXPjijjjiji为在Y=yj条件下随机变量X的条件分布律。 ) () () | (BPABPBAP 同理，对于固定的i，若PX=xi0，则称 ., 2 , 1,| jppxXPyYxXPxXyYPiijijiij为在X=xi条件下随机变量Y的条件分布律。 2. 条件分布函数 xxjijjYXiyYxXPyYxXPyxF|)|(|jxxijxxjijppppii ) () () | (BPABPBAP同理： iyyijiXYppxyFj)|

4、(|例1 二维离散型随机变量(X,Y)的分布律如表 XYX1= -1 X2=1 X3=2 Y=0 1/12 0 3/12 Y=3/2 2/12 1/12 1/12 Y=2 3/12 1/12 0求条件分布律PX=xi|Y=2. ) () () | (BPABPBAP解：X与Y的边缘分布如表： XYx1=-1 x2 =1 x3 =2 p.j y1=0 1/12 0 3/12 4/12 y2 =3/2 2/12 1/12 1/12 4/12 y3=2 3/12 1/12 0 4/12 pi . 6/12 2/12 2/12 4/12 PX=-1|Y=2=p13/p. .3=3/4；PX=1|Y=2

5、=p23/p. .3=1/4；PX=2|Y=2=p33/p. .3=0；又如：PX=1|Y=0=p21/p. .1=0等；) () () | (BPABPBAP PX=-1|Y=2=p13/p. .3=3/4；PX=1|Y=2=p23/p. .3=1/4；PX=2|Y=2=p33/p. .3=0；进一步可求)2|(| YxFYX 11114310)2|(|xxxYxFYX) () () | (BPABPBAP例2: 一射手进行射击,击中目标的概率为p(0p1) ,射击到击中的目标两次为止.设以X表示首次击中目标所进行的射击次数,以Y表示总共进行的射击次数,试求X和Y的联合分布律及条件分布律.

6、解:按题意Y=n 就表示在第n次射击时击中目标,且在第1次,第2次,第n-1次射击中恰有一次击中目标. 已知各次射击是相互独立的,于是不管m(m0 ,于是对于任意x有,| yYyPyYyxXPyYyxXP 上式给出了在任意y-Yy+下X的条件分布函数,现在我们引入以下的定义. ) () () | (BPABPBAP1.条件分布函数的定义：给定y,设对于任意实数x,若极限 ,lim|lim00 yYyPyYyxXPyYyxXP 存在,则称此极限为在条件Y=y下X的条件分布函数, 记为PXx|Y=y或记为FX|Y(x|y). 2公式： 设(X,Y)的分布函数为F(x,y)，概率密度为f(x,y).

7、若在点(x,y)处f(x,y), fY(y)连续,且fY(y)0,则有 ) () () | (BPABPBAP,lim)|(0| yYyPyYyxXPyxFYX xYYXYxYXduyfyufyxFyfduyufyxF)(),()|()(),()|(|或写成或写成，亦即亦即)()(),(),(lim0 yFyFyxFyxFYY 2/)()(2/),(),(lim0 yFyFyxFyxFYY)(),(yFdydyyxFY ) () () | (BPABPBAP3.条件概率密度 定义)(),()|(|yfyxfyxfYYX 同理，)(),()|(|xfyxfxyfXXY 称为在Y=y条件下X的条件

8、概率密度，且满足概率密度的两个性质。 称为在X=x条件下X的条件概率密度，且满足概率密度的两个性质。 yXXYYXdvxfvxfxyFxyF)(),()|()|(|和和类类似似地地可可以以定定义义) () () | (BPABPBAP例1: 设(X,Y)服从二维正态分布 N(1,2,12,22,),求在X=x的条件下,Y的条件密度函数fY|X(y|x).解: (X,Y)的密度函数为 )()(2)()1(21exp121),(2222212121212221 yyxxyxf yx，由上一节的例知道 21212)(121)( xXexf所以X=x条件下Y的条件概率密度为 ) () () | (BP

9、ABPBAP 12)(exp121)(),()|(2222112222| xyxfyxfxyfXXY这正是正态分布 )1,(2221122 xN) () () | (BPABPBAP例2: 设数X在区间(0,1)上随机地取值,当观察到X=x(0 x1)时,数Y在区间(x,1)上随机取值.求Y的概率密度fY(y). 解: 按题意X具有概率密度 其它其它0101)(xxfX 对于任意给定的值x(0 x1),在X=x的条件下,Y的条件概率密度 其它其它0111)|(|yxxxyfXY于是得联合概率密度为 其它01011),(yxxyxf) () () | (BPABPBAP于是得关于Y的边缘概率密度

10、为 其它其它010)1ln(11),()(0yydxxdxyxfyfyY) () () | (BPABPBAP例3:设(X,Y)的概率密度为 其它其它042 , 0, 0)24(163),(yxyxyxyxf求:(1) fY|X(y|x)；(2)PY2|X=1/2。 解：(1)先求X的边缘概率密度。 其它020)2(83)24(163),()(2402xxdyyxdyyxfxfxX当0 x2时， 其它其它0240)2(224)(),()|(2|xyxyxxfyxfxyfXXY) () () | (BPABPBAP 其它其它因为因为0309)3(2| )|()21|()2(21|yyxyfxyfxXYXY 。所所以以91392)21|(21|2322| dyydyxyfXYPXY) () () | (BPABPBAP小结小结 （以连续型（以连续型r.v为例）为例）概念概念 联合联合p.d 边缘边缘p.d 条件