2012年高中数学 1.3.1 单调性与最大（小）值课件 新人教A版必修1

1、1.3.1 单调性与最大（小）值单调性与最大（小）值).()(),()()()(,:)(21212121减减函函数数上上是是增增函函数数在在区区间间那那么么就就说说函函数数时时，都都有有，当当值值上上的的任任意意两两个个自自变变量量的的内内某某个个区区间间如如果果对对于于定定义义域域的的定定义义域域为为一一般般地地，设设函函数数DxfxfxfxfxfxxxxDIIxf 定义定义:复习提问复习提问 如果如果y=f(x)在某个区间是增函数或减函数在某个区间是增函数或减函数,那么那么就说函数就说函数y=f(x)在这一区间具有（严格的）在这一区间具有（严格的）单调性单调性，这一区间叫做这一区间叫做y=

2、f(x)的的单调区间单调区间.函数单调性的定义：函数单调性的定义：证明函数单调性的方法步骤证明函数单调性的方法步骤 1. 任取任取x1，x2D，且，且x1x2；2. 作差作差f(x1)f(x2)；3. 变形（通常是因式分解和配方）；变形（通常是因式分解和配方）；4. 定号（即判断差定号（即判断差f(x1)f(x2)的正负）；的正负）；5.下结论（即指出函数下结论（即指出函数f(x)在给定的区间在给定的区间D上的上的单调性）单调性） 利用定义证明函数利用定义证明函数f(x)在给定的区间在给定的区间D上的单上的单调性的一般步骤：调性的一般步骤：12,(0),xx ， + +12121211()()

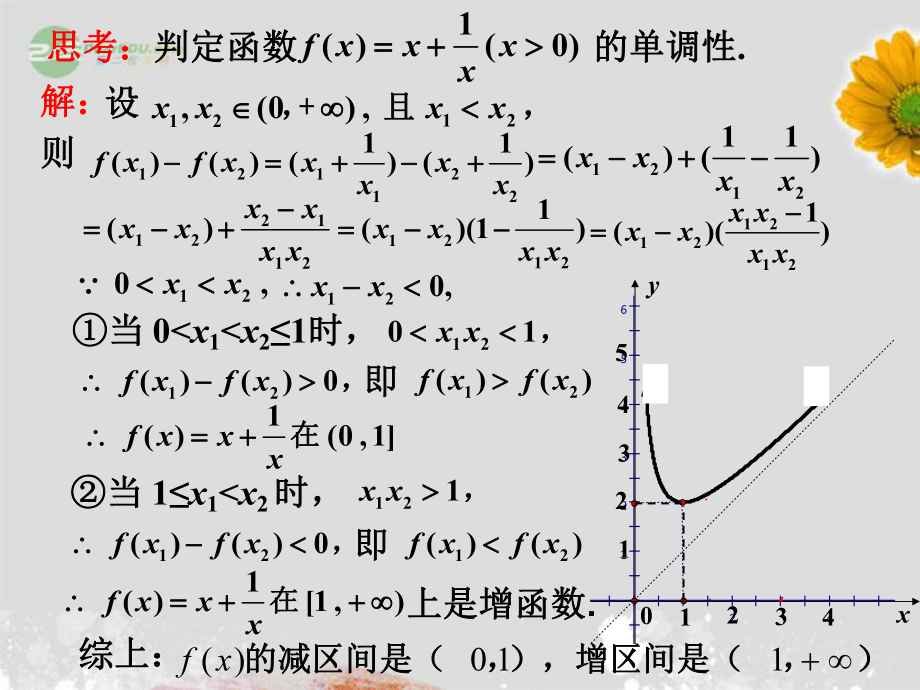
3、()()f xf xxxxx121211()()xxxx120,xx解：解：则则211212()xxxxx x 12121()(1)xxx x1212121()()x xxxx x 120,xx12()()0f xf x ，12()()f xf x 1( )(0 ,1f xxx在在即即1201x x ，思考：思考：判定函数判定函数 的单调性的单调性.1( )(0)f xxxx12xx 且且，设设 当当 0 x1x21时，时，当当 1x1x2 时，时，121x x ，12()()0f xf x ，12()()f xf x 即即1( )1,)f xxx 在在上是增函数上是增函数.654321-1-

4、2-3-4-8-6-4-224681012xy1234102345综上：综上：），），增增区区间间是是（，的的减减区区间间是是（110)(xf函数单调性的应用 求最大最小值 比较大小 解不等式 例例1.1.画出函数画出函数 图象，图象，2( )23( 2 2)f xxxx ，解：解：2( )(1)4( 2 2)f xxx ，并根据图象说出并根据图象说出f(x)的单调区间，以及在每一单调区的单调区间，以及在每一单调区间上，间上，f(x)是增函数还是减函数是增函数还是减函数. .由由f(x)的图象知该函数单调区间有：的图象知该函数单调区间有：-2 , 1 , 1 , 2.其中其中f(x)在区间在区

5、间-2 , 1上是增函数，上是增函数，问：问：f(x)在在-2 , 2上有最值吗上有最值吗？当当x=1时，时，答：答：f(x)有最大值有最大值 4；当当x=-2时，时， f(x)有最小值有最小值 -5. .在区间在区间1 , 2上是减函数上是减函数. .最大值最大值 一般地，设函数一般地，设函数y=f(x)的定义域为的定义域为I，如果，如果存在实数存在实数M满足：满足： （1）对于任意的）对于任意的xI，都有，都有f(x)M; （2）存在）存在x0I，使得，使得f(x0) = M .那么称那么称M是函数是函数y=f(x)的的最大值最大值. . 最小值最小值 一般地，设函数一般地，设函数y=f(

6、x)的定义域为的定义域为I，如果，如果存在实数存在实数M满足：满足： （1）对于任意的）对于任意的xI，都有，都有f(x)M; （2）存在）存在x0I，使得，使得f(x0) = M .那么称那么称M是函数是函数y=f(x)的的最小值最小值. . max( )f xM 记作：记作：min( )f xM 记作：记作：例例2. .求函数求函数 在区间在区间2，6上的最大值和上的最大值和最小值最小值 12xy解解:121222()()11f xf xxx由由2x1x26 ,12()()0,f xf x所以，函数所以，函数 是区间是区间2,6上的减函数上的减函数.12xy且且 x10, 于是于是 (x1

7、-1)(x2-1)0,12 ()()f xf x 即即故当故当x=2时，时，max2y ；当当x=6时，时，min0.4.y 设设 x1 , x2 2,6，例例3. .求函数求函数 的最值的最值 32xxy5)(,5)(minmaxxfxf例例4. .求函数求函数 在区间在区间 上的最大上的最大最小值最小值 322xxy3,26)3()(; 2) 1 ()(maxminfxffxf例例5. .若函数若函数 在区间在区间 上的最小值是上的最小值是f(1),f(1),求求 的取值范围的取值范围. .bxaxy)1(232) 1 ,(a2a思考：2) 3-()(, 1)2()2(0) 1 (1).()()(0,0)(xfxfffyfxfxyfyxxf解不等式解不等式如果如果证明：证明：）都有）都有，（