X射线的衍射强度

1、第三章第三章 X X射线衍射强度射线衍射强度3-1 3-1 引言引言 X X射线衍射分析晶体结构所需的信息：射线衍射分析晶体结构所需的信息： 衍射方向衍射方向: : 反映晶胞的大小和形状因素，可以反映晶胞的大小和形状因素，可以 用用BraggBragg方程描述。方程描述。 衍射强度衍射强度: : 反映晶体的原子种类以及原子在晶反映晶体的原子种类以及原子在晶 胞中的位置不同。胞中的位置不同。 可以进行合金的定性分析、定量分析、固溶体可以进行合金的定性分析、定量分析、固溶体 点阵有序化，点阵畸变等。点阵有序化，点阵畸变等。X X射线衍射强度，在衍射仪上反映的是衍射峰的高低或衍射峰射线衍射强度，在衍

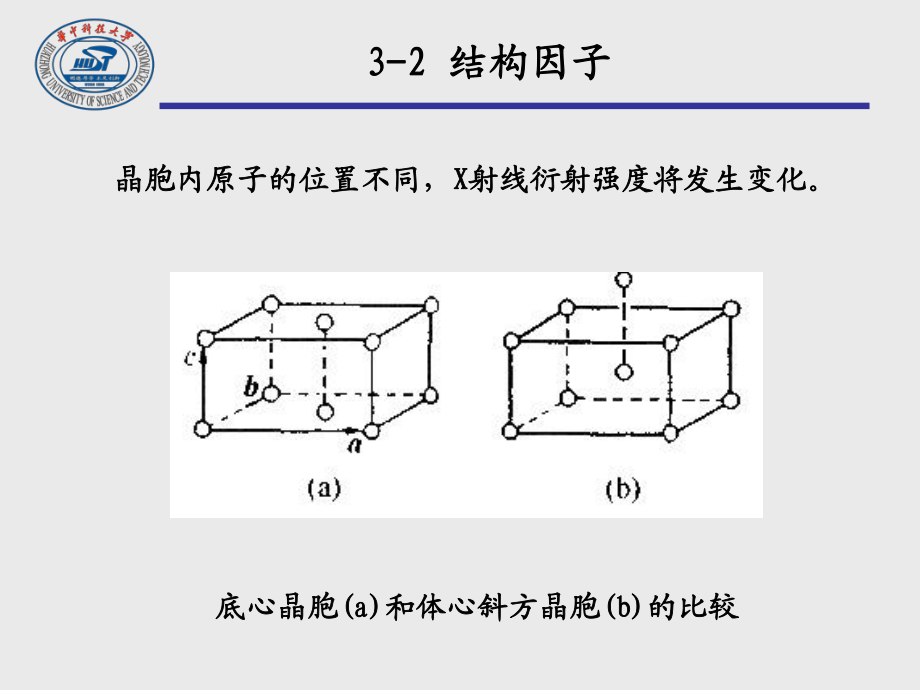
2、射仪上反映的是衍射峰的高低或衍射峰所包围面积的大小。严格的说，是在单位时间内通过与衍射所包围面积的大小。严格的说，是在单位时间内通过与衍射方向相垂直面积上的方向相垂直面积上的X X射线光量子的数目。射线光量子的数目。一般而言，一般而言， X X射线衍射强度取相对值，即同一衍射线谱的强度之比。射线衍射强度取相对值，即同一衍射线谱的强度之比。X射线衍射强度射线衍射强度 3-2 3-2 结构因子结构因子晶胞内原子的位置不同，晶胞内原子的位置不同，X X射线衍射强度将发生变化。射线衍射强度将发生变化。底心晶胞底心晶胞(a)(a)和体心斜方晶胞和体心斜方晶胞(b)(b)的比较的比较系统消光系统消光：原子

3、在晶体中位置不同或原子种类不同而引起的某些方向上：原子在晶体中位置不同或原子种类不同而引起的某些方向上 的衍射线消失的现象。的衍射线消失的现象。结构因子：结构因子：定量表征原子排布以及原子种类对衍射强度影响规律的参定量表征原子排布以及原子种类对衍射强度影响规律的参 数，即晶体结构对衍射强度的影响因子。数，即晶体结构对衍射强度的影响因子。晶胞内原子位置发生变化，将使衍射强度减小甚至消失，这说明晶胞内原子位置发生变化，将使衍射强度减小甚至消失，这说明BraggBragg方程是反射的方程是反射的必要条件必要条件，而不是，而不是充分条件充分条件。底心晶胞底心晶胞(a)(a)和体心斜方晶胞和体心斜方晶胞

4、(b)(001)(b)(001)面的衍射面的衍射 结构因子结构因子各种因素对各种因素对X X射线衍射强度的影响。射线衍射强度的影响。v 一个电子对X射线的散射v 一个原子对X射线的散射v 一个晶胞对X射线的散射v 一个小晶体对X射线的散射v 多晶体的衍射强度X射线衍射强度的影响因素射线衍射强度的影响因素一个电子对一个电子对X X射线的散射射线的散射一、相干散射一、相干散射电子散射的电子散射的X X射线的射线的强度大小强度大小I Ie e与与入射束的强度入射束的强度I I0 0和和散射角度散射角度有关。一有关。一个电子将个电子将X X射线散射后，强度射线散射后，强度I Ie e可以表示为：可以表

5、示为：R: R: 电场中任意一点到发生散射电子的距离电场中任意一点到发生散射电子的距离( (观测距离观测距离) )。 2 2：电场中任意一点到原点连线与入射：电场中任意一点到原点连线与入射X X射线方向的夹角。射线方向的夹角。r re e: : 经典电子半径。经典电子半径。2.822.821010-5 -5 m me:e:电子电荷，电子电荷，m:m:电子质量，电子质量，0 0：真空介电常数：真空介电常数 c:c:光速光速22cos1)(220RrIIee2204eermc 以上的公式是一个电子对以上的公式是一个电子对X X射线散射的汤姆孙射线散射的汤姆孙( J.J.Thomson)( J.J.

6、Thomson)公式，电子对公式，电子对X X射线散射的特点：射线散射的特点：公式讨论公式讨论1 1）散射线强度很弱。）散射线强度很弱。2 2）散射强度与观测点距离的平方称反比。）散射强度与观测点距离的平方称反比。1cm1cm处处I Ie e/I/I0 0仅为仅为1010-26-263 3）入射）入射X X射线经过电子散射后，其散射强度在空间的各个方向射线经过电子散射后，其散射强度在空间的各个方向 上变得不同，称为偏振化。偏振化的程度取决于上变得不同，称为偏振化。偏振化的程度取决于2 2角度。角度。偏振因子或极化因子：偏振因子或极化因子：21 cos 22 一个电子对一个电子对X射线的散射强度

7、是射线的散射强度是X射线散射强度的自然单位，其单位为射线散射强度的自然单位，其单位为J/(m2.s)。对散射强度的定量处理取相对强度已经足够用。对散射强度的定量处理取相对强度已经足够用。二、二、康普顿康普顿- -吴有训散射吴有训散射X X射线使电子具有动能，自己变成波长更长的量子射线使电子具有动能，自己变成波长更长的量子并且偏离原来的方向。入射并且偏离原来的方向。入射X X射线与散射射线与散射X X射线存在射线存在波长之差。也称为非相干散射。波长之差。也称为非相干散射。康普顿散射不能产生衍射现象，它的存在将给衍射康普顿散射不能产生衍射现象，它的存在将给衍射图象带来有害的背底，应设法避免它的出现

8、图象带来有害的背底，应设法避免它的出现。 一个电子对一个电子对X X射线的散射射线的散射一个原子对一个原子对X X射线的散射射线的散射 当当X X射线与一个原子相遇，原子系统中的原子核和电子射线与一个原子相遇，原子系统中的原子核和电子都将发生受迫振动，由于原子核的质量远大于电子，据汤都将发生受迫振动，由于原子核的质量远大于电子，据汤姆逊公式，其发生的散射过程可以忽略。姆逊公式，其发生的散射过程可以忽略。 如果假定原子中所含的如果假定原子中所含的Z Z个电子都集中在一点，则各个个电子都集中在一点，则各个电子散射波之间将不存在相位差，可以简单地叠加。电子散射波之间将不存在相位差，可以简单地叠加。

9、一般一般X X射线所用的波长与原子直径同为一个数量级，因射线所用的波长与原子直径同为一个数量级，因此，不能认为原子中的电子都集中在一点。此，不能认为原子中的电子都集中在一点。 实际上，原子中的电子是按照电子云状态分布在原子空实际上，原子中的电子是按照电子云状态分布在原子空间的不同位置上，故各个电子散射波之间是存在位相差的，间的不同位置上，故各个电子散射波之间是存在位相差的，这一位相差使得合成波的强度减弱。这一位相差使得合成波的强度减弱。X X射线受到一个原子的散射射线受到一个原子的散射一个原子对一个原子对X X射线的散射射线的散射一个电子对一个电子对X X射线散射后空间某点强度可用射线散射后空

10、间某点强度可用I Ie e表示，那么一个表示，那么一个原子对原子对X X射线散射后该点的强度射线散射后该点的强度I Ia a：2aeIfIf f 是原子散射因子，它反映了各个电子散射波的位相差之后，是原子散射因子，它反映了各个电子散射波的位相差之后，原子中所有电子散射波合成的结果。原子中所有电子散射波合成的结果。由于电子波合成时要有损耗，所以，由于电子波合成时要有损耗，所以，f fZZ。经过修正：经过修正：一个原子对一个原子对X X射线的散射射线的散射acAfA一个原子的散射波振幅一个电子的散射波振幅原子散射因子可表明某原子散射波的振幅相当于原子散射因子可表明某原子散射波的振幅相当于电子散射波

11、振幅的若干倍。电子散射波振幅的若干倍。原子散射因子可以描述某种原子在给定条件下的原子散射因子可以描述某种原子在给定条件下的散射散射“效率效率”。一个原子对一个原子对X X射线的散射射线的散射 原子散射因子曲线原子散射因子曲线对于不同类型的原子，其原子散射因子对于不同类型的原子，其原子散射因子 f 是可变的，它与是可变的，它与sin和和有关。随有关。随sin/的值的增大而变小。的值的增大而变小。 Sin0时，时，f=Z.原子序数越小，非相干散射越强。（核外电子所占比例增大）原子序数越小，非相干散射越强。（核外电子所占比例增大）一个原子对一个原子对X X射线的散射射线的散射一个晶胞对一个晶胞对X

12、X射线的散射射线的散射预备知识：预备知识：X X射线的波前电场强度随时间的变化可以用周期函数表示：射线的波前电场强度随时间的变化可以用周期函数表示：111222sin(2)sin(2)EAtEAt位相和振幅不同的正弦波的合成位相和振幅不同的正弦波的合成X X射线波的复数表示方法：射线波的复数表示方法：cossiniAeAAi(cossin )iAeAAi多个向量可以写成：多个向量可以写成：X X射线的波强度正比于振幅的平方，为：射线的波强度正比于振幅的平方，为：22iiiAeAe AeA一个晶胞对一个晶胞对X X射线的散射射线的散射假设该晶胞由假设该晶胞由n n种原子组成，各原子的：种原子组成

13、，各原子的： 单位晶胞的原子单位晶胞的原子1 1、2 2、3 3n n的坐标为的坐标为u u1 1v v1 1w w1 1、 u u2 2v v2 2w w2 2、 u u3 3v v3 3w w3 3 u un nv vn nw wn n ； 散射因子为：散射因子为：f f1 1 、f f2 2 、f f3 3 .f .fn n； 各原子的散射波与入射波的位相差各原子的散射波与入射波的位相差为：为： 1 1 、2 2 、3 3 . . n n ；晶胞内所有原子对相干散射波的合成波振幅晶胞内所有原子对相干散射波的合成波振幅A Ab b：11221(.)jniiiibennejjAAf ef e

14、f eAf e一个晶胞对一个晶胞对X X射线的散射射线的散射其中晶胞中所有原子散射波叠加的波即为结构因子，用其中晶胞中所有原子散射波叠加的波即为结构因子，用F F表示：表示：1jnibjjeAFf eAbeAFA一个晶胞内所有原子散射的相干散射波振幅一个电子的散射波振幅可以证明，可以证明，hklhkl晶面上的原子（坐标为晶面上的原子（坐标为uvwuvw）与原点处原子经）与原点处原子经hklhkl晶面反晶面反射后的位向差射后的位向差，可以由反射面的晶面指数和坐标，可以由反射面的晶面指数和坐标uvwuvw来表示：来表示：2()1jjjni hukvlwhkljjFf e对于一个对于一个hklhkl

15、晶面的结构因子晶面的结构因子,F,F为：为：22（hu+kv+lwhu+kv+lw）一个晶胞对一个晶胞对X X射线的散射射线的散射 结构因子表征了晶胞内原子种类、原子结构因子表征了晶胞内原子种类、原子 个数、原子位置对衍射强度的影响。个数、原子位置对衍射强度的影响。 结构因子与晶胞的形状和大小无关结构因子与晶胞的形状和大小无关! !结构因子与晶胞的关系结构因子与晶胞的关系 结构因子结构因子F FHKLHKL 的讨论的讨论晶胞中（晶胞中（H K LH K L）晶面的衍射强度：）晶面的衍射强度：2eaHKLIFI关于结构因子关于结构因子：2jjjjhukvlw其中其中: u: uj j、v vj

16、j、w wj j是是j j原子的阵点坐标原子的阵点坐标. . H K L H K L是发生衍射的晶面。是发生衍射的晶面。 产生衍射的充分条件：产生衍射的充分条件：满足布拉格方程且满足布拉格方程且F FHKLHKL00 简单晶胞的结构因子简单晶胞的结构因子在简单点阵中，每个晶胞中只包含在简单点阵中，每个晶胞中只包含一个原子，位于坐标原点一个原子，位于坐标原点000000处。处。2(0.0.0. )22ihklFfeFf结论：结论：预备知识：3524611iiiiiieeeeee 简单晶胞底心斜方晶胞底心斜方晶胞的结构因子的结构因子每个晶胞中有每个晶胞中有2 2个同类原子，其坐标分别为个同类原子，

17、其坐标分别为000000和和1/2 1/2 01/2 1/2 0，原子散射因子相同，都为原子散射因子相同，都为f fa a112( .0. )2(0.0.0. )222(0)2 2(1)ihklihklh kiFfefeFfe 底心斜方晶胞底心斜方晶胞当当H+KH+K为偶数时，即为偶数时，即H H，K K全为奇数或全为偶数，（如全为奇数或全为偶数，（如111111，112112，113113，021021等，与等，与l l的取值无关）。的取值无关）。2224FfFfH, K为同性数当当H+KH+K为奇数时，即为奇数时，即H H，K K有一个奇数，一个偶数，（如有一个奇数，一个偶数，（如0010

18、01，012012，013013，101101等）。等）。0F H, K为异性数在底心斜方晶胞中，在底心斜方晶胞中，F FHKLHKL不受不受L L的影响，只有当的影响，只有当H H、K K全为奇数或全为偶数时才能产生衍射。全为奇数或全为偶数时才能产生衍射。底心斜方晶胞底心斜方晶胞的结构因子的结构因子体心立方晶胞的结构因子体心立方晶胞的结构因子每个晶胞中有每个晶胞中有2 2个同类原子，其坐标为个同类原子，其坐标为000000和和1/2 1/2 1/2 1/2 1/2 1/2 ，其原子散射因子其原子散射因子f f 相同相同: :1112( . )2(0.0.0. )()2221ihklihkli

19、 h k lFfefefe 2224FfFf0F （h+k+l）为偶数（h+k+l）为奇数体心点阵中，只有当体心点阵中，只有当H+K + LH+K + L为为偶数时才能产生衍射偶数时才能产生衍射体心立方每个晶胞中有每个晶胞中有4 4个同类原子，分别位于个同类原子，分别位于000000、1/2 1/21/2 1/2 0 0、 1/2 0 1/2 1/2 0 1/2 ，0 1/2 1/20 1/2 1/2面心立方晶胞的结构因子面心立方晶胞的结构因子1111112( . )2( . )2( . )2(0.0.0. )222222()()()1ihkiklihlihkli h ki k li h lF

20、fefefefefeee22416FfFf0F h,k,l为同性数h,k,l为异性数在面心立方中，只有当在面心立方中，只有当H H、K K、L L全为全为奇数或全为偶数时才能产生衍射。奇数或全为偶数时才能产生衍射。面心立方四种基本点阵的消光规律四种基本点阵的消光规律布拉菲点布拉菲点阵阵出现的反射出现的反射消失的反射消失的反射简单点阵简单点阵全部全部无无底心点阵底心点阵H H、K K全为奇数或全为偶数全为奇数或全为偶数H H、K K奇偶混奇偶混杂杂体心点阵体心点阵H+K+LH+K+L为偶数为偶数H+K+LH+K+L为奇数为奇数面心点阵面心点阵H H、K K、L L全为奇数或全为偶数全为奇数或全为

21、偶数H H、K K、L L奇偶奇偶混杂混杂课堂习题课堂习题具有面心立方结构的具有面心立方结构的Si元素，其晶胞参数如下：元素，其晶胞参数如下：点阵常数点阵常数a=0.54nm，单胞有，单胞有4个原子，分别位于个原子，分别位于0 00，1/2 1/2 0，1/2 0 1/2，0 1/2 1/2，试求，试求CuK射线得到射线得到X射线衍射图谱中最初射线衍射图谱中最初3条衍射线的位置，条衍射线的位置，必须考虑衍射线条结构消光的影响。必须考虑衍射线条结构消光的影响。2/110. 022454. 0077. 02/154. 02/222222 nmlkhadnm（422）为例：）为例：习题答案习题答案面

22、心立方结构物质面心立方结构物质(fcc(fcc) )体心立方结构物质体心立方结构物质(bcc)(bcc)超点阵衍射斑点超点阵衍射斑点假设晶胞内有异种原子存在，必须在假设晶胞内有异种原子存在，必须在F F的求和公式的求和公式中考虑各原子的原子散射因子中考虑各原子的原子散射因子f f不相同这一因素。因不相同这一因素。因而消光规律和衍射强度都发生变化。而消光规律和衍射强度都发生变化。实验中经常出现在某一合金上原来不存在的衍射实验中经常出现在某一合金上原来不存在的衍射线，经过热处理形成长程有序后出现超点阵衍射斑线，经过热处理形成长程有序后出现超点阵衍射斑点，这就是晶胞内出现异种原子所引起的。点，这就是

23、晶胞内出现异种原子所引起的。 结构因子应用举例有序固溶体分析结构因子应用举例有序固溶体分析 CuCu3 3AuAu在高温下系无序固溶体，当温度低于在高温下系无序固溶体，当温度低于T Tc c（有序（有序无序转无序转变温度）点阵中各原子重新排列，呈现某种规律，即有序化，变温度）点阵中各原子重新排列，呈现某种规律，即有序化，此时称之有序固溶体，经过有序化的固溶体点阵称之超点阵此时称之有序固溶体，经过有序化的固溶体点阵称之超点阵或超结构。或超结构。（1 1）完全无序）完全无序每个晶胞中含有四个平均原子（每个晶胞中含有四个平均原子（0.75 Cu+0.25Au0.75 Cu+0.25Au）属面心）属面

24、心立方点阵。坐标立方点阵。坐标000 1/2 1/2 0 1/2 0 1/2 0 1/2 1/2000 1/2 1/2 0 1/2 0 1/2 0 1/2 1/2 F FHKLHKL=f=f平均平均1+ei(H+K)+ei(H+L)+ei(K+L) 1+ei(H+K)+ei(H+L)+ei(K+L) 当当H H、K K、L L全为奇数或全为偶数时全为奇数或全为偶数时 FHKL=4 fFHKL=4 f平均平均=fAu+3fCu=fAu+3fCu 当当H H、K K、L L为奇偶混杂时，为奇偶混杂时， F FHKLHKL=0 =0 消光消光有序固溶体分析有序固溶体分析 2 2）当完全有序）当完全有

25、序 AuAu占据坐标占据坐标000 Cu000 Cu占据坐标：占据坐标： 1/2 1/21/2 1/2 0 0， 1/2 0 1/2 0 ， 0 1/2 1/20 1/2 1/2 F FHKLHKL=fAu+ fCu ei(H+K)+ei(H+L)+ei(K+L=fAu+ fCu ei(H+K)+ei(H+L)+ei(K+L) 当当H H、K K、L L全为奇数或全为偶数时全为奇数或全为偶数时 F FHKLHKL=fAu+3fCu=fAu+3fCu 当当H H、K K、L L为奇偶混杂时为奇偶混杂时 F FHKLHKL=fAu-fCu0=fAu-fCu0基本线条、超点阵线条。超点阵线条的存在是

26、有序化有力证基本线条、超点阵线条。超点阵线条的存在是有序化有力证据，它的强度变化确定合金的长程有序度。据，它的强度变化确定合金的长程有序度。有序固溶体分析有序固溶体分析 3-3 3-3 多晶体的衍射强度多晶体的衍射强度为了计算衍射线强度，首先要求出结构因子。对于多为了计算衍射线强度，首先要求出结构因子。对于多晶粉末，影响晶粉末，影响X X射线强度的因子有五项。射线强度的因子有五项。 结构因子结构因子 角因子角因子( (包括极化因子和罗仑兹因子包括极化因子和罗仑兹因子) ) 多重性因子多重性因子 吸收因子（平面状和圆柱状样品的吸收）吸收因子（平面状和圆柱状样品的吸收） 温度因子温度因子多重性因子

27、多重性因子晶体中晶面距相同、晶面上原子排列规律相同的晶晶体中晶面距相同、晶面上原子排列规律相同的晶面，称为等同晶面。面，称为等同晶面。在多晶衍射中，等同晶面的所有成员都有机会参与在多晶衍射中，等同晶面的所有成员都有机会参与衍射，这些晶面对应的衍射角衍射，这些晶面对应的衍射角22都相等，形成一个都相等，形成一个衍射锥。衍射锥。一个晶面族中，等同晶面越多，参与衍射的概率就一个晶面族中，等同晶面越多，参与衍射的概率就越大，这个晶面族对衍射强度的贡献也就越大。越大，这个晶面族对衍射强度的贡献也就越大。把把同族晶面同族晶面HKLHKL的等同晶面数的等同晶面数P P称为衍射强度的多重称为衍射强度的多重因子

28、。因子。各晶面族的多重因子列表各晶面族的多重因子列表 晶系晶系指数指数H000K000LHHHHH0HK00KLH0LHHLHKLP 立方立方6812242448菱方、六方菱方、六方6261224 正方正方4248816 斜方斜方248 单斜单斜2424 三斜三斜222角因子之罗仑兹因子角因子之罗仑兹因子罗仑兹因子是考虑影响衍射线强度的一些几何因素：罗仑兹因子是考虑影响衍射线强度的一些几何因素： 晶粒大小对强度的影响晶粒大小对强度的影响 晶粒数目的影响晶粒数目的影响 衍射线位置对强度测量的影响衍射线位置对强度测量的影响以上三种几何因子影响均于布拉格角有关，称为：以上三种几何因子影响均于布拉格角

29、有关，称为：罗仑兹因子罗仑兹因子()() 晶粒大小对强度的影响晶粒大小对强度的影响 1) 1) 晶体很薄时的衍射强度晶体很薄时的衍射强度在严格的布拉格角情况下，对于在严格的布拉格角情况下，对于晶体的某些晶面将会出现消光。晶体的某些晶面将会出现消光。( (晶体为无穷大时晶体为无穷大时) )但晶体很薄，晶面数目很少，相但晶体很薄，晶面数目很少，相消过程不完全，结果某些本应相消过程不完全，结果某些本应相消的衍射线将会重新出现。消的衍射线将会重新出现。 晶粒大小对强度的影响晶粒大小对强度的影响 在稍微偏离布拉格角情况下，在稍微偏离布拉格角情况下，将导致强度减弱的衍射线出将导致强度减弱的衍射线出现。现。

30、如果晶面数少，则布拉格角如果晶面数少，则布拉格角偏到很大仍有衍射线强度。偏到很大仍有衍射线强度。实际晶体的衍射强度曲线（实际晶体的衍射强度曲线（a a）和理想状态下衍射强度曲线（）和理想状态下衍射强度曲线（b)b)的比较的比较影响衍射峰宽的因素：影响衍射峰宽的因素：1 1）X X射线不是绝对平行，存在较小的发散角。射线不是绝对平行，存在较小的发散角。 2 2） X X射线不是单色的。射线不是单色的。3 3）仪器宽化。）仪器宽化。 4 4）内应力造成的宽化。）内应力造成的宽化。 5 5）晶粒细小造成的宽化。）晶粒细小造成的宽化。 晶粒大小对强度的影响晶粒大小对强度的影响 晶体二维方向很小时的衍射

31、强度晶体二维方向很小时的衍射强度当晶体转过一个很小的角度，当当晶体转过一个很小的角度，当时，衍射线依然存在，可以推时，衍射线依然存在，可以推导出使衍射线消失的条件：导出使衍射线消失的条件：()2sin()2sinaabbNNNN为晶面长度为晶面宽度一个小晶体在三维方向的衍射强度：一个小晶体在三维方向的衍射强度：23cossinsin2bacIItN NV称为第一几何因子，它反映了晶粒大小对衍射强度的影响。称为第一几何因子，它反映了晶粒大小对衍射强度的影响。参加衍射晶粒的数目的影响参加衍射晶粒的数目的影响衍射强度正比于参加衍射衍射强度正比于参加衍射晶粒的数目。参与衍射的晶粒的数目。参与衍射的晶粒

32、数目与试样中总晶粒晶粒数目与试样中总晶粒数目之比就等于环带的面数目之比就等于环带的面积与整个球的面积之比。积与整个球的面积之比。 2/cos4)90sin(2*2*drrdrqq称为第二几何因子称为第二几何因子粉末多晶衍射的强度粉末多晶衍射的强度 cos I衍射线位置对强度测量的影响衍射线位置对强度测量的影响单位弧长的衍射强度，单位弧长的衍射强度，I I单位单位= =衍射环上总强度衍射环上总强度/ /（2Rsin22Rsin2）即：即： ，称为第三几何因子。，称为第三几何因子。 2sin/1 I罗仑兹极化因子罗仑兹极化因子22(1 cos 2 )( )sin.cos 罗仑兹极化因子罗仑兹极化因

33、子()()：罗仑兹因子罗仑兹因子23cossinsin2bacIItN NV cos I 2sin/1 I cossin412sin1cos2sin12 I吸收因子吸收因子试样本身对试样本身对X X射线的吸收会造成衍射强度的衰减，一般用吸射线的吸收会造成衍射强度的衰减，一般用吸收因子来收因子来A()A()描述：描述：121( )() exp()iVIASSdVIVA()A()的值与入射的值与入射X X射线的波射线的波长及样品的形状、大小、线长及样品的形状、大小、线吸收系数有关。吸收系数有关。V V： 试样的体积试样的体积S1S1、S2S2：入射线和衍射线的路径：入射线和衍射线的路径i i :

34、: 试样的线吸收系数试样的线吸收系数 试样吸收的影响试样吸收的影响VeRVssl)(21)(圆柱形试样的吸收因子圆柱形试样的吸收因子 R( R() ) 平板试样的吸收因数平板试样的吸收因数平板试样的吸收因数与布拉平板试样的吸收因数与布拉格角无关。格角无关。 200abIdII 温度因子温度因子温度的变化实际上影响原子在平衡位置的热振动。原子热温度的变化实际上影响原子在平衡位置的热振动。原子热振动的结果使点阵中原子排列周期性部分被破坏，即衍射振动的结果使点阵中原子排列周期性部分被破坏，即衍射条件部分破坏，造成衍射强度的降低，而且将在非布拉格条件部分破坏，造成衍射强度的降低，而且将在非布拉格方向产生散射，这种现象称之热漫散射。方向产生散射，这种现象称之热漫散射。 有热振动影响时的衍射强度温度因子无热振动理想情况下的衍射强度MTeIID2M:与热振动振幅和散射角有关的系数。与热振动振幅和散射角有关的系数。1 1）衍射角）衍射角一定时，温度越高，衍射强度一定时，温度越高，衍射强度I I 随之减小。随之减小。2 2）温度）温度T T一定时，衍射角一定时，衍射角越大，衍射强度越大，衍射强度I I 随之减小。随之减小。原子振动的振幅不单纯是温度的函数，还与材料的原子振动的振幅不单纯是温度的函数，