杆件的强度、刚度和稳定性介绍

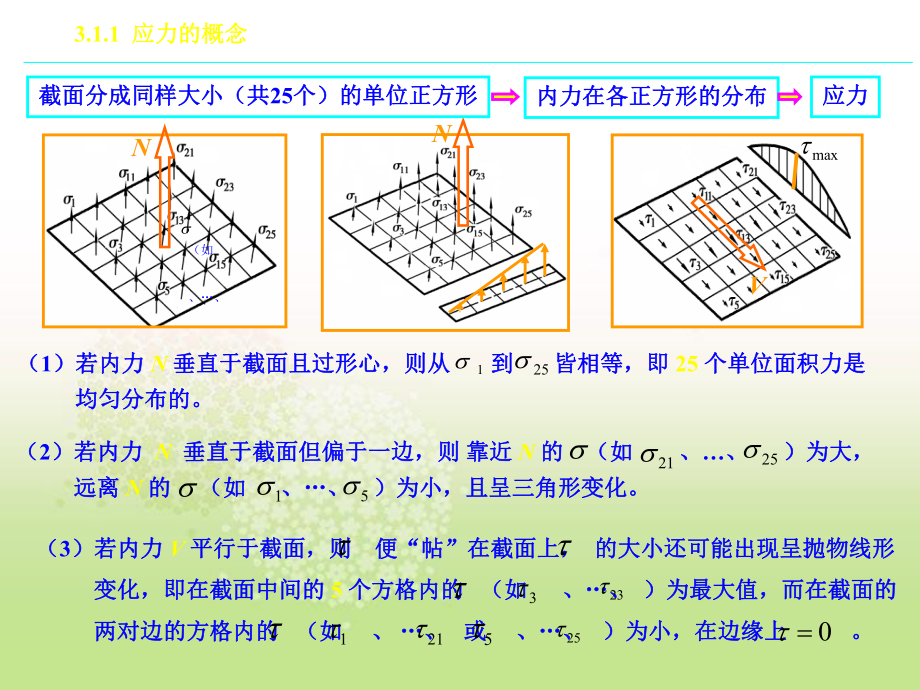
1、杆件的强度、刚度和稳定性杆件的强度、刚度和稳定性介绍介绍第第3 3章杆件的强度、刚度和稳定性章杆件的强度、刚度和稳定性 3.1应力与强度应力与强度 问题引入问题引入细杆细杆粗杆粗杆（有关）（有关）杆之截面杆之截面形状大小形状大小（轴力（轴力 N （轴力（轴力 N 钢杆钢杆（材料相同）（材料相同）（粗细一致）（粗细一致）细杆易断细杆易断粗杆难断粗杆难断钢杆钢杆 难断难断木杆木杆 易断易断杆之材料杆之材料（有关）（有关）杆之截面杆之截面形状大小形状大小杆之杆之材料材料截面截面材料材料3.1.1 应力的概念应力的概念 NNVmax截面分成同样大小（共截面分成同样大小（共25个）的单位正方形个）的单位

2、正方形内力在各正方形的分布内力在各正方形的分布应力应力（如、（2）若内力）若内力 N 垂直于截面但偏于一边，则垂直于截面但偏于一边，则 靠近靠近 N 的的 （如（如 、 ）为大，）为大， 远离远离 N 的的 （如（如 、 ）为小，且呈三角形变化。）为小，且呈三角形变化。212515（1）若内力）若内力 N 垂直于截面且过形心，则从垂直于截面且过形心，则从 到到 皆相等，即皆相等，即 25 个单位面积力是个单位面积力是 均匀分布的。均匀分布的。 125（3）若内力）若内力 V 平行于截面，则平行于截面，则 便便“帖帖”在截面上，在截面上， 的大小还可能出现呈抛物线形的大小还可能出现呈抛物线形 变

3、化，即在截面中间的变化，即在截面中间的 5 个方格内的个方格内的 （如（如 、 ）为最大值，而在截面的）为最大值，而在截面的 两对边的方格内的两对边的方格内的 （如（如 、 、 或或 、 ）为小，在边缘上）为小，在边缘上 。3231215250讨论：讨论： NNVmax（如 应力是单位面积上的力，单位面积力的数值之和应力是单位面积上的力，单位面积力的数值之和截面上的合力。截面上的合力。如均匀分布的如均匀分布的 应力应力 （ ），截面面积为），截面面积为 A，轴向内力为，轴向内力为 N，则则 ，或，或 。2512ANAN 当当 A 越小，在越小，在 N 不变之下，不变之下， 分布的密集程度就越高

4、，即数值越大，反之亦然。分布的密集程度就越高，即数值越大，反之亦然。 故应力为内力在一点处的集度。故应力为内力在一点处的集度。 应力应力 垂直于截面的应力垂直于截面的应力平行于截面的应力平行于截面的应力正应力，与正应力，与 N 相同正负号相同正负号 。剪应力，与剪应力，与 V 相同正负号相同正负号 。 应力单位：牛顿应力单位：牛顿/ /米米2（N/ /m2），用），用“帕（帕（Pa）”示之，即示之，即1Pa1N/ /m2。1KPa103Pa103N/ /mm2；1MPa106Pa1N/ /mm2；1GPa109Pa103N/ /mm2。如何通过改变几何形状或尺寸，来改变应力的大小？如何通过改变

5、几何形状或尺寸，来改变应力的大小？体重体重 W 不变，脚下的应力可随鞋与地面的接触面积不同而改变。不变，脚下的应力可随鞋与地面的接触面积不同而改变。 雪橇鞋雪橇鞋 高背软椅的低应力使人感到舒适，而硬板凳的高应力却使人不爽。高背软椅的低应力使人感到舒适，而硬板凳的高应力却使人不爽。 大头盖使拇指产生舒适应力，针尖产生非常高的应力大头盖使拇指产生舒适应力，针尖产生非常高的应力图钉一按即图钉一按即硬板凳硬板凳abcd3.1.2 轴向拉（压）杆的应力及强度计算轴向拉（压）杆的应力及强度计算 1) )轴向拉（压）杆的应力轴向拉（压）杆的应力N拉伸前拉伸前画两线段画两线段 、abcd 和和 仍然保持直线仍

6、然保持直线 纵向伸长量纵向伸长量 都相同都相同ba dcl平面假设：平面假设：变形前横截面为平面，变形后仍保持为平面，且垂直于杆轴线变形前横截面为平面，变形后仍保持为平面，且垂直于杆轴线平面平面假设假设纵向伸长纵向伸长 l 相同相同abcd拉伸后拉伸后，ba abdccdlN 轴力；轴力；A 横截面积；横截面积； 正应力正应力(拉为拉为正正，压为，压为负负)各点各点内力相等内力相等应力应力均匀分布均匀分布AN讨论：讨论： 对于变截面杆（对于变截面杆（ A 非常量），非常量）， 所在截面的应力不一定为最大，因还需所在截面的应力不一定为最大，因还需 考虑考虑 A 是否为最小。是否为最小。 maxN

7、 对于等直杆，当对于等直杆，当 N 不变时，若杆截面（不变时，若杆截面（A）细小，则就大，细杆易断；）细小，则就大，细杆易断； 当轴向外力较多时，应求得最大轴力当轴向外力较多时，应求得最大轴力 ，此时，此时 。maxNANmaxmax3m4m 【例例3. .1】在例在例2.2.2中，砖柱上段截面尺寸为中，砖柱上段截面尺寸为 240mm 240mm，承受荷，承受荷 P1 1=50kN；下段下段 370mm 370mm，承受荷载，承受荷载 P2100kN，现试求各段之应力。，现试求各段之应力。【解解】 （1）作轴力图）作轴力图 AB段段：A1240 240mm57600mm2（2）求应力）求应力M

8、Pa87. 0N/mm87. 057600105023111ANMPa1 . 1N/mm1 . 11369001015023222AN注意：计算时，将轴力注意：计算时，将轴力 N 的正负号代入，结果为正则为拉应力，负即为压应力。的正负号代入，结果为正则为拉应力，负即为压应力。AB段：段：kN501NBC段：段：kN1502NBC段：段：A2370 370mm136900mm2N 图图【例例3. .2】图图 (a) 为一斗式提升机。斗与斗之间用链条连接，链条的计算简图如图为一斗式提升机。斗与斗之间用链条连接，链条的计算简图如图(b)所示，每个料斗连同物料的总重量所示，每个料斗连同物料的总重量 P

9、=2000N。钢链由两层钢板构成，如图。钢链由两层钢板构成，如图(c)所示。所示。每个链板厚每个链板厚 t =4.5mm，宽，宽 h = 40mm，高，高H =65mm，钉孔直径，钉孔直径 d=30mm。试求链板的。试求链板的最大应力。最大应力。 【解解】（1）求轴力并画轴力图）求轴力并画轴力图 （2）求应力）求应力: : 腰部：腰部：A12ht =2 40mm 4.5mm 360mm2孔处：孔处：A22(H- -d) t =2 （65- -30）mm 4.5mm =315mm2MPa1 .38N/mm1 .383152000622maxmaxANN 图图(a)(b)(c)最大轴力最大轴力 N

10、max= 6 P最大应力在链最大应力在链条的钉孔之处条的钉孔之处材料名称材料名称牌号牌号容许应力容许应力低低 碳碳 钢钢Q235170170100低合金钢低合金钢Q345230230140灰口铸铁灰口铸铁3454160200混凝土混凝土C200.447混凝土混凝土C300.610.3松、杉（顺纹）松、杉（顺纹）578121栎木、桦木等（顺纹）栎木、桦木等（顺纹）810121622) )强度条件强度条件最大应力与材料强度最大应力与材料强度 比较比较杆是否会因强度不足而破坏杆是否会因强度不足而破坏 判断判断等截面轴向拉（压）杆的强度条件：等截面轴向拉（压）杆的强度条件： 注：maxmaxAN 材料

11、在拉伸（压缩）时的容许应力。材料在拉伸（压缩）时的容许应力。 为容许压应力；表表3. .1常用材料的容许应力值（常用材料的容许应力值（MPa）（适用于常温、静荷载和一般工作条件下的杆）（适用于常温、静荷载和一般工作条件下的杆）轴向拉伸轴向拉伸为容许拉应力； 为容许剪应力。轴向压缩轴向压缩受剪受剪已知内力、材料（已知内力、材料（ 、 ），根据强度条件选），根据强度条件选 。 maxNA ANmaxmax（1）强度校核：）强度校核： 已知材料、尺寸（、）和所受之荷载（），校核杆已知材料、尺寸（、）和所受之荷载（），校核杆之强度是否满足要求。之强度是否满足要求。 AmaxN ANmaxmax若若 ，

12、则杆满足强度要求，则杆满足强度要求 max若若 ，则杆之强度就不够，则杆之强度就不够 max问题：问题：欲使欲使 ，可，可 ，但不经济；有时可稍大于，但不能超过，但不经济；有时可稍大于，但不能超过5%。 maxAmax maxNA （2）截面选择：）截面选择：（3）容许荷载：）容许荷载：已知材料、尺寸（、），根据强度条件确定已知材料、尺寸（、），根据强度条件确定 。 AmaxN ANmax3) )强度计算强度计算之截面为危险截面之截面为危险截面maxN 为材料的容许应力为材料的容许应力强度计算强度计算三种类型三种类型强度条件强度条件安全安全不安全不安全由可选型钢（工字钢、槽钢、角钢）之型号由可

13、选型钢（工字钢、槽钢、角钢）之型号A（内力与荷载关系）（内力与荷载关系）结构的最大容许荷载结构的最大容许荷载?？ 【例例3. .3】现有一高度为现有一高度为 24m 的正方形截面花岗岩石柱，在其顶部作用一轴向荷载的正方形截面花岗岩石柱，在其顶部作用一轴向荷载P1000 kN。已知石材容重。已知石材容重 ，容许压应力，容许压应力 1 MPa，现要设计石柱，现要设计石柱所需的截面尺寸，分两种情况：（所需的截面尺寸，分两种情况：（1）柱为等值杆；（）柱为等值杆；（2）柱分为三段的阶梯形杆。）柱分为三段的阶梯形杆。3kN/m28l = 24 m自自重重【解解】 1.计算轴力计算轴力 用横截面用横截面

14、nn ，在距顶端为，在距顶端为 x 处截杆，并取处截杆，并取上部分为对象。上部分为对象。 nnx由平衡方程：由平衡方程：由由（A）式可得轴力图。式可得轴力图。)()()(xAPxWPxN（A） 2. .设计横截面设计横截面（1）等直杆的柱）等直杆的柱)(maxlAPN由由（A）式知，当式知，当 xl 时，时， 。 根据强度条件有根据强度条件有maxmaxlAPANlPA（B） 2363m324102810101000lPA取取 a =1.8 m，则，则 。2m24. 3A正方形截面的边长正方形截面的边长 ，m73. 13 Aa（2）阶梯形的柱）阶梯形的柱比较：比较： 与与 ，对于受拉（压）的等

15、直杆，对于受拉（压）的等直杆，当考虑自重作用时，相当于从材料的容许应力当考虑自重作用时，相当于从材料的容许应力 里减去里减去 。若为变截面杆（如若为变截面杆（如 阶梯形），则柱顶的力应分段计算。阶梯形），则柱顶的力应分段计算。maxNAllPA第第 1 柱段：柱段：236311m29. 18102810101000lPA取，则。取，则。 m2 . 11a21m44. 1A正方形截面边长正方形截面边长 ：m14. 129. 111Aa第第 2 段柱：段柱：作用在第作用在第 2 段柱面上的力为段柱面上的力为 ，则，则11lAP 236332112m7 . 11028101

16、000llAPA取取 ，则，则 。 m4 . 12a22m96.1A正方形截面边长正方形截面边长 ：m3 . 17 . 122Aa第第 3 段柱：段柱：23633322113m27. 281028108)96. 144. 1 (1028101000llAlAPA正方形截面边长正方形截面边长 ： ，取，取 ，则，则 。m51. 127. 233Aam6 . 13a23m56. 2A3. .等直柱与阶梯柱用材比较等直柱与阶梯柱用材比较设等直柱和梯形柱体积为设等直柱和梯形柱体积为 、 1V2V31m76.772424. 3lAV33212m68.478)56. 296. 144. 1 (3)(lAA

17、AV阶梯柱省材阶梯柱省材 3.1.3 梁的正应力及强度计算梁的正应力及强度计算 1) )分析梁的变形分析梁的变形mmnnaabbmmnnaabbO1O2中性层中性层中性轴中性轴zy（1）在加）在加 M 前，画两横向线前，画两横向线 和和 ， 代代 表两横截面；在两横向线间，又画两条表两横截面；在两横向线间，又画两条 纵向线纵向线 和和 。mmnnaabb（2）在加）在加 M 后，梁发生弯曲变形后，梁发生弯曲变形 。 两横向线两横向线 、 ，仍保持直线，只是倾，仍保持直线，只是倾 斜了微小角度，即横截面仍然保持平面。斜了微小角度，即横截面仍然保持平面。mmnn 两纵向线两纵向线 和和 都变成了弧

18、线，都变成了弧线， 缩短缩短 伸长。伸长。aabbaabb 在在 与与 之间，有一弧线之间，有一弧线 ，它既没，它既没 缩短也不伸长。缩短也不伸长。aabb21oo（3）与）与 为同一纵向纤维层，即为中性层，其为同一纵向纤维层，即为中性层，其 横截面上的轴为中性轴。此处的中性层之上横截面上的轴为中性轴。此处的中性层之上 为受压区，之下为受拉区。为受压区，之下为受拉区。21oo受压区受压区受拉区受拉区2) )纯弯曲的正应力公式纯弯曲的正应力公式(- -)(+)y中性层中性层中性层中性层中性层之上（中性层之上（下下）的各）的各纤维层纤维层 缩短缩短 （伸长伸长 ），），离离 越远，其越远，其 缩短

19、缩短（伸长伸长 ）量就越大。）量就越大。 21oo应力和变形成正比，在应力和变形成正比，在梁的梁的上上（下下）边缘，其）边缘，其压压（ 拉拉 ）应力为）应力为最大最大；在中性层处，应力为在中性层处，应力为零零。 设横截面上的中性轴设横截面上的中性轴为为 z ，在与，在与 z 的距离的距离为为 y 处的任一点的应处的任一点的应力为力为 。 zIyM中性轴中性轴zI 截面的惯性矩。截面的惯性矩。 梁在纯弯曲段内，梁的横截面上的弯矩梁在纯弯曲段内，梁的横截面上的弯矩 M 为一常数。为一常数。 b 沿梁宽沿梁宽 b 的各点正应力的各点正应力 ，其，其 y 值若相同，则值若相同，则 值就不变。值就不变。

20、 当当 y0 时，即在中性轴上，时，即在中性轴上， ；当；当 时，即在梁的上下时，即在梁的上下 边缘，边缘， 压（拉）应力的绝对值皆为最大。压（拉）应力的绝对值皆为最大。 0maxyy讨论讨论3) )惯性矩惯性矩 Iz截面几何性质截面几何性质 惯性矩惯性矩 Iz截面的形状和尺寸截面的形状和尺寸取决于取决于梁的承载能力将不同梁的承载能力将不同不同不同 Izbhzzbh立立放放平平放放矩形截面对矩形截面对 z 轴轴惯性矩惯性矩 Iz = b h3 / /12矩形截面对矩形截面对 z 轴轴惯性矩惯性矩 Iz = h b3 / /12结论：结论：同样一根梁，在同样的荷载作用下，立放时其承载能力比平放时

21、要强。同样一根梁，在同样的荷载作用下，立放时其承载能力比平放时要强。hb大大小小123zbhI 123yhbI 644yzdII等截面梁（等截面梁（Iz 不变）不变）梁又是纯弯曲（梁又是纯弯曲（M 不变）不变）ymax 和和 Iz 同属于截面几何性质，把两者归类，即令，则同属于截面几何性质，把两者归类，即令，则maxzzyIW 最大正应力最大正应力 发生发生 在离中性轴最远（在离中性轴最远（ y ymax ）的边缘处）的边缘处 maxzmaxmaxIyMzmaxWMWz 为抗弯截面模量。若为抗弯截面模量。若Wz 愈大，则愈大，则 就愈小，梁的抗弯性能就愈好，反之亦然，就愈小，梁的抗弯性能就愈好

22、，反之亦然，故故 Wz 又称为截面抵抗矩，单位为又称为截面抵抗矩，单位为 m3。max对于矩形截面，若对于矩形截面，若 ，且，且 ，则，则123zbhI 2maxhy621223maxzzbhhbhyIW对于圆形截面，若对于圆形截面，若 ，且，且 ，则，则644zdI2maxdy3226434maxzzdddyIW4) )横力弯曲的正应力公式横力弯曲的正应力公式弯矩弯矩 M 沿梁的轴线沿梁的轴线 x 是变化的是变化的 Mmax最大弯矩最大弯矩 Mmax 所在的横截面，其应力比其它截面的应力都要大，属于所在的横截面，其应力比其它截面的应力都要大，属于危险截面危险截面。 zmaxmaxWMMmax

23、=M=0M=000max)(max横力弯曲的正应力公式：横力弯曲的正应力公式：且离中性轴最远（且离中性轴最远（yymax）的边缘处。）的边缘处。 结论：结论：中性轴中性轴max在危险截面（即在危险截面（即Mmax 所在横截面）上，所在横截面）上，梁的梁的)(max ZWMmaxmaxymax（1）强度条件强度条件)()(材料抗弯容许应力材料抗弯容许应力强度条件变成：强度条件变成：脆性材料：脆性材料： ，为达到材尽其用，常用上下不对称之截面。，为达到材尽其用，常用上下不对称之截面。)(1max1max)max(ZZWMIyM)(2max2max)max(ZZWMIyM此时，同一截面则有两个抗弯截

24、面模量，此时，同一截面则有两个抗弯截面模量， 且较小者，其应力较大。且较小者，其应力较大。（2）强度计算）强度计算 强度校核强度校核 截面选择截面选择 许可荷载许可荷载5) )强度条件及计算强度条件及计算)(maxzyCy1)(max maxMWZMmaxy2三类问题三类问题)()( ZWM max满足者，则安全，否则不安全。满足者，则安全，否则不安全。截面形状及尺寸。截面形状及尺寸。荷载最大值。荷载最大值。 【例例3. .4】如图所示楼板主梁为工字型钢。已知集中荷载如图所示楼板主梁为工字型钢。已知集中荷载 P75kN，跨度，跨度 l10m，钢的材料抗弯容许应力钢的材料抗弯容许应力 152MP

25、a，试选择工字钢截面的型号。，试选择工字钢截面的型号。lmkN375maxM【解解】梁的两端具有稍为转动及伸缩的可能，梁的两端具有稍为转动及伸缩的可能，故梁计算简图可视为简支梁，故梁计算简图可视为简支梁， maxM33663maxZcm2467m1024671015210375 MW1. .求求先求出先求出 A、B 两处的支座反力：两处的支座反力：YAYB（375）/ /2112.5 kN再画出梁的弯矩图，最大弯矩在为再画出梁的弯矩图，最大弯矩在为ZW2. .求求3. .选型号选型号查查 附录附录3 型钢表，选型钢表，选 56b 号工字钢，得号工字钢，得 Wx2447cm3 Wz=2467cm

26、3但相差不到但相差不到1%，故可用。故可用。 【例例3.53.5】矩形截面的简支木梁，已知矩形截面的简支木梁，已知 l = =4m，b= =120mm，h= =180mm，q= =5.1kN/m， 木材的容许应力木材的容许应力=10MPa。试校核梁的强度。试校核梁的强度。 4633mm1032. 581218012012bhIZ4633mm1032. 581218012012bhIZ【解解】1.计算截面几何特征量计算截面几何特征量366mm10648. 0901032.582hIWZZmaxM2.求求mmN1010.2mkN2 . 104 1 . 58181622max l qMMPa8.15

27、mmmmN10648.0102.10366maxmaxZWM3.强度校核强度校核MPa10 36maxmm1002. 1102 .10MWZ故不安全，应重新设计截面。故不安全，应重新设计截面。4.截面重设截面重设23bh取取322916) 32 (6hhhbhWZ（为什么？）（为什么？）北宋李诫北宋李诫营造法式营造法式：“凡梁之大小，随其广高为三分，以二分为厚凡梁之大小，随其广高为三分，以二分为厚”61002. 1q l 2/ /8h = = 300mmb = = 200mm3.1.4 梁的剪应力及强度计算梁的剪应力及强度计算横力弯曲横力弯曲 正应力正应力 剪应力剪应力 弯矩弯矩 M + 剪力

28、剪力V （内力）（内力）？1) )矩形截面梁的剪应力矩形截面梁的剪应力max立立体体图图平平面面图图y0抛物线抛物线横截面，当横截面，当 y0，；当，；当 ，或，或 。2hy )(max)(maxbhV23max横截面，当横截面，当 y = =0， ，当，当， 。 2 hy 0zmaxmaxWM比比较较危险截面危险截面bhVmaxmax23危险截面危险截面任意荷载任意荷载任一横截面任一横截面【例例3. .6】图为一矩形截面悬臂梁，试比较横截面内发生的最大剪应力和最大正应力。图为一矩形截面悬臂梁，试比较横截面内发生的最大剪应力和最大正应力。bhPbhV2323maxmaxV 图图62zbhWM

29、图图Mmax=P l【解解】1. .作作 V 图和图和 M 图图最大负弯矩发生在梁的根部，最大负弯矩发生在梁的根部，MmaxPl 。所有横截面上，剪力值恒定，所有横截面上，剪力值恒定，VmaxP，2. .求最大剪应力求最大剪应力2zmaxmax6bhplWM3. .求最大正应力求最大正应力因矩形截面的抵抗矩因矩形截面的抵抗矩 ，故有，故有 )(41maxmaxlhmax4. .比较比较max 和和 之比为之比为梁高跨比的四分之一梁高跨比的四分之一 一般一般情况情况细长梁的细长梁的 h/ /l 1/ /5 ，则，则 不会超不会超过过 之值的之值的 1 / /20 。 故对一般梁故对一般梁（非短粗

30、梁或非薄壁梁），其强度（非短粗梁或非薄壁梁），其强度只按正应力计算，不必考虑剪应力只按正应力计算，不必考虑剪应力max2) )薄壁截面梁的剪应力薄壁截面梁的剪应力薄壁薄壁h1上翼缘上翼缘下翼缘下翼缘腹板腹板maxmax壁厚比宽和高要小得多壁厚比宽和高要小得多工字形、工字形、T形和圆环形等薄壁截面梁形和圆环形等薄壁截面梁工字形截面：上、下翼缘工字形截面：上、下翼缘 很小，不计。腹板为矩形，在中性轴（很小，不计。腹板为矩形，在中性轴（z 轴）有轴）有 ，且，且 与与 相差相差 很小很小 ，故视为均匀分布：，故视为均匀分布： minmin1max11maxmaxAVhbVmaxminmax（A1为腹

31、板的面积）为腹板的面积）腹板腹板T形截面：其腹板与工字形的腹板类似，形截面：其腹板与工字形的腹板类似， 在截面的中性轴（在截面的中性轴（z 轴）之上。轴）之上。 23maxmaxbhV圆环形截面圆环形截面 ： 还是发生在中性轴（还是发生在中性轴（z 轴）之上。轴）之上。 23maxmaxbhVMPa11 MPa11 3) )强度条件及计算强度条件及计算MPa2 . 1 材料在纯剪切时的容许剪应力材料在纯剪切时的容许剪应力 梁的剪应力强度条件：梁的剪应力强度条件： 对于矩形截面的等直梁，其强度条件：对于矩形截面的等直梁，其强度条件： 【例例3.7】一矩形截面简支木梁，梁上作用有均布荷载一矩形截面

32、简支木梁，梁上作用有均布荷载 q。已知：。已知：l4m，q4kN/m，弯曲时材料的容许拉应力弯曲时材料的容许拉应力 ，容许剪应力，容许剪应力 ；若取截面的高宽比为；若取截面的高宽比为 3/2，试确定矩形截面的高和宽。，试确定矩形截面的高和宽。3363maxzm10727. 01011108MW332210727. 0836)23(6bbbbhWzm125. 0bV 图图m187. 0hM 图图【解解】 1. .画出画出V 图、图、M 图图 2. .由正应力强度条件确定由正应力强度条件确定 b、h 梁所需的抗弯截面模量：梁所需的抗弯截面模量：23bh1.2MPa MPa486. 019. 013

33、. 010823233maxmaxbhV而而lll1aaa1又又，取，取b13 cm，h19 cm3. .验算剪应力强度条件：验算剪应力强度条件：满足满足 3.2杆件的变形与刚度杆件的变形与刚度 问题引入问题引入杆杆件件变形是否过大？变形是否过大？杆件是否破坏？杆件是否破坏？刚度条件刚度条件取决于取决于强度条件强度条件取决于取决于？问题：问题：杆件的变形应如何确定？其量值怎样计算？何谓刚度条件？杆件的变形应如何确定？其量值怎样计算？何谓刚度条件？ 3.2.1 拉（压）杆的轴向变形拉（压）杆的轴向变形虎克定律虎克定律 llaallaa1) )纵向变形纵向变形杆原杆原长长 l杆的纵向变形（伸长或缩

34、短）为杆的纵向变形（伸长或缩短）为轴向轴向力力P伸长伸长缩短缩短内力内力变形变形外力外力作用作用杆长杆长为为 l101aaa拉伸：拉伸：l 0 压缩：压缩：l 0 2) )横向变形横向变形设原横向尺寸为设原横向尺寸为 a，变形后为，变形后为 a1，则杆横向总变形为：，则杆横向总变形为： 01aaa拉伸：拉伸：a 0 压缩：压缩：a0 00较粗较粗较细较细3) )线应变线应变 问题：问题：纵向伸长纵向伸长 l 为杆的总变形量，反映不了杆的变形程度。为杆的总变形量，反映不了杆的变形程度。 试试验验拉伸拉伸橡皮筋橡皮筋长长 度度 l 长度长度 l/ /2伸长伸长l相同相同变细程度小（变细程度小（较粗

35、较粗）变细程度大（变细程度大（较细较细）变形程度变形程度与与 l 有关有关 纵向纵向应变应变l / / l 是相对变形，称是相对变形，称线应变线应变，是一无量纲的量。，是一无量纲的量。 l 是绝对变形，量纲为是绝对变形，量纲为长度长度，单位为，单位为m 或或 mm； llaa拉伸时拉伸时a 1 a压缩时压缩时a1 a 横向横向应变应变 拉伸：拉伸：压缩：压缩：AlNl 拉（压）杆的与拉（压）杆的与 的正负号总是相反的！的正负号总是相反的！ANEll1或或（为泊松比）（为泊松比） EAl Nl应力不超过应力不超过 材料比例极限材料比例极限4) )应力和应变关系应力和应变关系虎克定律虎克定律 杆伸

36、长或压缩杆伸长或压缩 的变形量的变形量 l 与轴力与轴力 N 和杆长和杆长 l 成正比成正比与杆截面的面积与杆截面的面积 A 成反比成反比E引人比例常数引人比例常数 E拉（压）杆虎克定律拉（压）杆虎克定律 讨论：讨论：（1）比例常数比例常数 E弹性模量弹性模量随材料而异随材料而异实验测定实验测定杆抗拉（压）的杆抗拉（压）的截面刚度截面刚度EA（2） A为杆的截面面积，故为杆的截面面积，故EA代表截面的刚度代表截面的刚度 两层两层含义含义若若EA 大，则大，则 l 小，小， EA为拉（压）刚度为拉（压）刚度 与与 之关系之关系) m( 0005. 0101020101002105062931 1

37、ABABAB A El Nl) m( 0001. 0101020101001 102062931 1BCBCBC A El Nl（3）) m( 0001. 0101020101001 102062931 1BCBCBC A El Nl) m( 000075. 0101020102001 103062931 2CDCDCD A El Nl) m(000375. 0101010102005 . 21030629322DEDEDEAEl NlDECDBCABlllll虎克定律虎克定律 结论：结论：在应力不超过比例极限时，应力和应变成正比，其比例常数为弹性模量在应力不超过比例极限时，应力和应变成正比，

38、其比例常数为弹性模量E。 （4）弹性弹性模量模量E 比例常数比例常数 E 是具有单位的量，故又称之为模量是具有单位的量，故又称之为模量 弹性是指外力撤消后，变形消失而恢复其原状弹性是指外力撤消后，变形消失而恢复其原状 单位单位GPa 【例例3. .8】由铜和钢组成的变截面杆，由铜和钢组成的变截面杆，AB段横截面面积段横截面面积A120102 mm2，DE段横段横截面面积截面面积A210102 mm2；铜的弹性模量；铜的弹性模量E1100 GPa，钢的弹性模量，钢的弹性模量E2200GPa。试求杆纵向总变形量试求杆纵向总变形量l。【解解】按按N、E、A 变化情况，分别计算每段长度的变化情况，分别

39、计算每段长度的 改变量，最后的代数和即为杆纵向总变形量改变量，最后的代数和即为杆纵向总变形量 l。 2. .求求各段的纵向伸长量或缩短量各段的纵向伸长量或缩短量1. . 画杆之轴力图画杆之轴力图000375. 0000075. 00001. 00005. 0)mm(15. 0)m(00015. 0BA（正值正值表示该段表示该段伸长伸长，负值负值表示该段表示该段缩短缩短） C3. .求求lCy故整根杆缩短了故整根杆缩短了0.15mm。CN 图图3.2.2 梁的弯曲变形及刚度校核梁的弯曲变形及刚度校核以悬以悬臂梁臂梁为例为例横看梁横看梁的截面的截面AB 轴线轴线为直线为直线变形前变形前挠曲线挠曲线

40、 连续连续光滑曲线光滑曲线变形后变形后横截面横截面形心形心 C变形前变形前横截面横截面形心形心A变形后变形后A x y平面内平面内转角转角 B挠度挠度 yC位移位移纵观梁纵观梁的轴线的轴线因设因设 y 轴轴向下为正向下为正规规定定讨论：讨论：（1）挠度的正负与单位）挠度的正负与单位（2）转角的正负与单位）转角的正负与单位单位常用单位常用 弧度弧度（rad）单位常取单位常取mm或或cm 转角转角顺顺时针为时针为正正逆逆时针为时针为负负B 挠度挠度向下向下为为正正向上向上为为负负过过 点作挠曲线的切线，则该切线点作挠曲线的切线，则该切线与与 x 轴的夹角恰好也是轴的夹角恰好也是 。 Bz2BA16

41、 EIPl1) )梁的转角、挠度和挠曲线方程梁的转角、挠度和挠曲线方程ymax20lxymax) 43 (4823zxlEIPxyz3max48 EIPly ) 43 (4823zxlEIPxyz3max48 EIPly )2(2433zxlxlEIqxyz3BA24 EIqlymaxz3max48 EIPly ymaxz3max48 EIPly z4max3845EIqly最大转角：最大转角：挠曲线方程：挠曲线方程：（ ）)3(6z2xlEIPxyz2B2 EIPl最大最大挠度：挠度：z3max3EIPly挠曲线方程：挠曲线方程：)46(2422z2lxlxEIqxyz3B6 EIql最大转

42、角：最大转角：最大挠度：最大挠度：z4max8 EIqly挠曲线方程：挠曲线方程：最大转角：最大转角：最大挠度：最大挠度：挠曲线方程：挠曲线方程：最大转角：最大转角：最大挠度：最大挠度：lx 0B4z3A124EIql（ ）z413845EIqlyC（ ）z413845EIqlyC（ ）z413845EIqlyCz2A216 EIPl2) )用叠加法计算梁的变形用叠加法计算梁的变形 【例例3. .9】一等截面简支梁，其上作用有集中荷载一等截面简支梁，其上作用有集中荷载 P 和均布荷载和均布荷载 q，求跨中，求跨中 C 点点的挠度和截面的挠度和截面 A 的转角。的转角。z32C48EIPlyz2

43、z3A2A1A1624 EIPlEIqlz3z4C2C1483845EIPlEIqlyyyCB【解解】 lflymaxf1000250 lllf受有多个受有多个荷载的梁荷载的梁叠加叠加转角转角挠度挠度荷载单独荷载单独作用的梁作用的梁转角转角挠度挠度0.01mmm10101034061020038464538456894z4maxEIqly0025. 0400100166. 0600001. 0maxlfly3) )梁的刚度校核梁的刚度校核梁的变形是否超过容许值梁的变形是否超过容许值 梁的刚度条件：梁的刚度条件： 刚度条件刚度条件梁的容许挠度梁的容许挠度 限值在限值在 范围内，规范对范围内，规范

44、对 值有具体规定。值有具体规定。MPa40mm5mm30梁应满足梁应满足强度条件强度条件一般一般情况情况控制作用控制作用从属地位从属地位先选择梁的截面先选择梁的截面再校核梁的刚度再校核梁的刚度 【例例3.10】现有一简支梁，已知：现有一简支梁，已知：l6m ，q4kN/ / m，f/ /l 1/400，由强度，由强度条件梁已选用条件梁已选用 22a 号工字钢，其弹性模量号工字钢，其弹性模量 E200GPa；试校核梁的刚度。；试校核梁的刚度。 【解解】查查附录附录3知，知，22a号工字钢的惯性矩号工字钢的惯性矩 IzIx3406cm4340610-8m4，在均布荷载在均布荷载 q 作用下的简支梁

45、，其最大挠度发生于跨中，且为作用下的简支梁，其最大挠度发生于跨中，且为mm2001lmm10002l故满足刚度要求。故满足刚度要求。3.3 压杆的稳定性分析压杆的稳定性分析问题引入问题引入N60005 3040 AP两根粗细一样，但长短不同之木杆，两根粗细一样，但长短不同之木杆，为什么长杆容易被折断？为什么长杆容易被折断？试验比较试验比较不同长细之杆的抗压能力不同长细之杆的抗压能力材料材料： 松木松木截面尺寸：截面尺寸：杆之长度：杆之长度：若按材料强度计算，则杆之抗压承载力为若按材料强度计算，则杆之抗压承载力为故杆之压力故杆之压力 6000N 时才会发生强度破坏时才会发生强度破坏问题：问题：强

46、度计算时，并没有考虑杆之长度，强度计算时，并没有考虑杆之长度，而而 l 对压杆承载力有无影响呢？对压杆承载力有无影响呢？rcN试验表明试验表明rcN22r c)( lEIN22r c)( lEIN结论：结论：压杆承载力为压杆承载力为 P2=30N3.3.1 压杆稳定性的概念压杆稳定性的概念 把压杆保持原有直线平衡状态的能力，称为压杆的稳定性，其破坏简称为把压杆保持原有直线平衡状态的能力，称为压杆的稳定性，其破坏简称为压杆失稳压杆失稳。压杆强度不足的破坏压杆强度不足的破坏压杆失稳的破坏压杆失稳的破坏有明显的先兆（比如变形过大，肉眼可见）有明显的先兆（比如变形过大，肉眼可见）无明显预兆的突然性破坏，其危害性更大无明显预兆的突然性破坏，其危害性更大加拿大魁北克大桥加拿大魁北克大桥下弦杆失稳下弦杆失稳 E突然倒塌突然倒塌 I脚手架失稳脚手架失稳l脚手架脚手架3.3.2 压杆的临界力及公式压杆的临界力及公式1) )压杆的临界力压杆的临界力临界力临界力N杆件材料杆件材料杆件尺