邮路规划和邮车调度的优化

1、邮路规划和邮车调度的优化一、问题的提出本题是2007年全国研究生数学建模竞赛 D题，题目如下：我国的邮政运输网络采用邮区中心局体制，即以邮区中心局作为基本封发单 元和网路组织的基本节点，承担着进、出、转口邮件的处理、封发和运输任务， 在此基础上组织分层次的邮政网。 邮路是邮政运输网络的基本组成单元,它是指 利用各种运输工具按固定班期、规定路线运输邮件，并与沿线有交接频次的邮政 局、所交换邮件总包所行驶的路线。邮路的结构形式有三种：辐射形、环形和混 合形。如图1所示，邮路A为一条环形邮路，邮路B为一条辐射形邮路。图1邮路示意图1、辐射形邮路：是指从起点局出发，走直线或曲折线的邮路，具特点是不 论

2、用一种或几种运输工具联运，从起点到终点后，仍按照原路线返回出发地点。 因此须在同一条路线上往返两个行程。这种邮路可以缩短运递时间，加快邮运 速度。但它的联系点较少，需用的运输工具较多，所耗费用较大。2、环形邮路：是指邮政运输工具走环形路线的邮路，即运输工具从起点出 发单向行驶，绕行一周，经过中途各站，回到出发地点。它的特点是不走重复 路线，联系点较多，运输工具的利用率高，运费也较省。但是邮件送到最后几 个交接点的时间较长。3、混合形邮路：是指包含辐射形和环形两种结构形式的邮路。某地区的邮政局、所分布如图2所示，分为地市中心局（简称地市局）、县 级中心局（简称县局）和支局三级机构，该地区的邮政运

3、输网络由区级邮政运 输网和县级邮政运输网构成。区级邮政运输网由从地市局出发并最终返回地市 局的区级邮车所行驶的全部邮路构成，县级邮政运输网由从县局出发并最终返 回县局的县级邮车所行驶的全部邮路构成。为使邮政企业实现低成本运营和较 高的服务质量，我们需要对该地区的邮政运输网络进行重构，确定合适的邮路 规划方案并进行邮车的合理调度。为了满足邮政的时限要求，必须尽可能地保证各县局、支局在营业时间内收寄的多数邮件能当天运送回地市局进行分拣封发等处理，以及每天到达地市 局的多数邮件能当天运送到目的地县局、支局。该地区从地市局到县局每天两 班车，从县局到支局每天仅有一班车。 该地区的邮政运输流程及时限规定

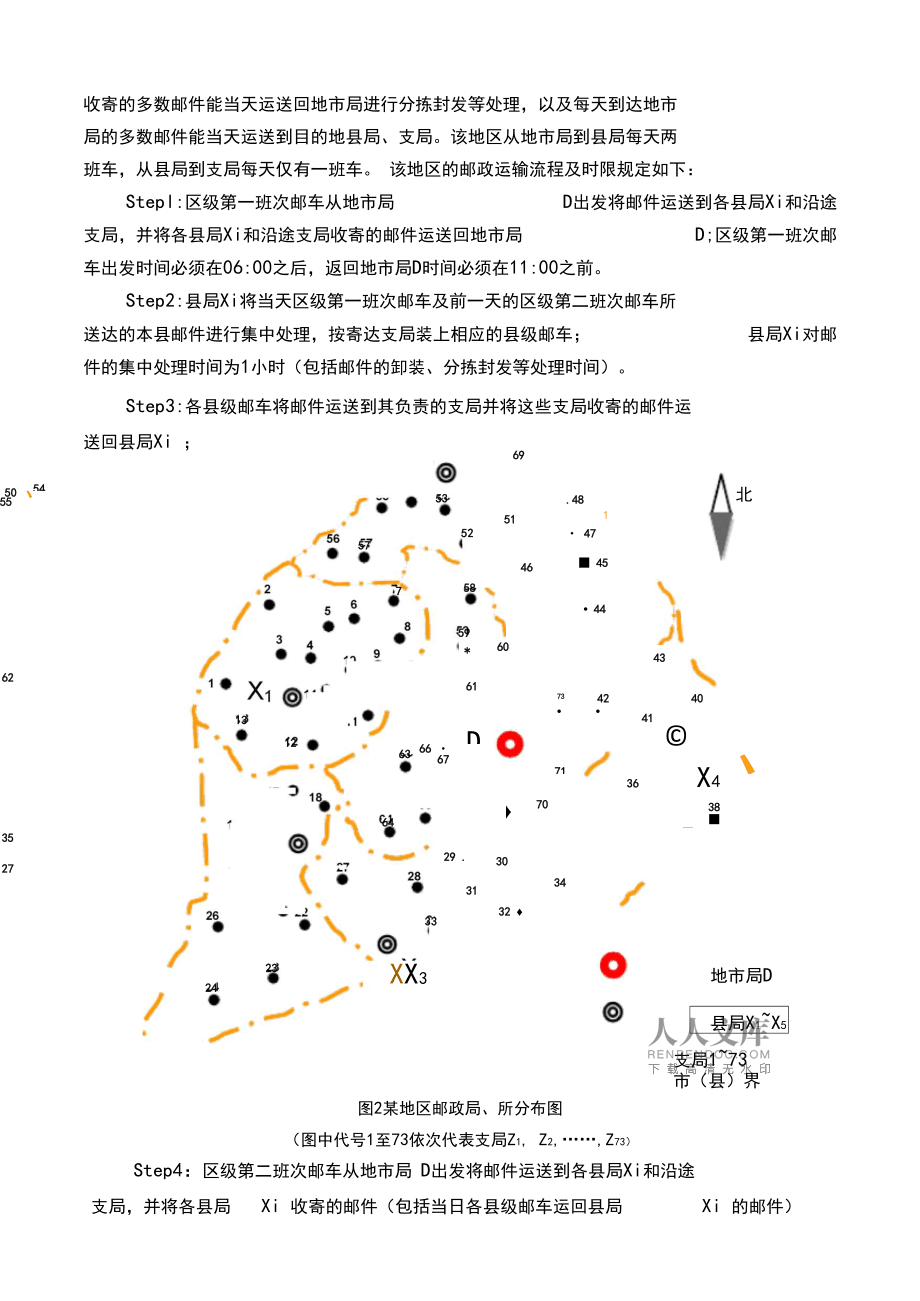
4、如下：Stepl:区级第一班次邮车从地市局 D出发将邮件运送到各县局Xi和沿途 支局，并将各县局Xi和沿途支局收寄的邮件运送回地市局 D;区级第一班次邮 车出发时间必须在06:00之后，返回地市局D时间必须在11:00之前。Step2:县局Xi将当天区级第一班次邮车及前一天的区级第二班次邮车所 送达的本县邮件进行集中处理，按寄达支局装上相应的县级邮车； 县局Xi对邮 件的集中处理时间为1小时（包括邮件的卸装、分拣封发等处理时间）。Step3:各县级邮车将邮件运送到其负责的支局并将这些支局收寄的邮件运送回县局Xi ；535157465876261D63706429 .273133XX323245

5、259*5455603032 66 67131214 *15 ®161117 19X220 .21” 222550 、4969656、.481 47 45 447342713534413643北40©X438 37 、39 .I地市局D县局X1X5支局173 市（县）界图2某地区邮政局、所分布图（图中代号1至73依次代表支局Z1, Z2,Z73）Step4：区级第二班次邮车从地市局 D出发将邮件运送到各县局Xi和沿途支局，并将各县局Xi 收寄的邮件（包括当日各县级邮车运回县局Xi 的邮件）和沿途支局收寄的邮件运送回地市局D;请注意区级第二班次邮车在县局Xi卸装完邮件后的出发

6、时间必须在县局Xi 的全部县级邮车返回县局并集中处理1小时以后，最终返回地市局D 的时间必须在18:00之前。假设区级两个班次邮车的行驶路线相同，要求区级邮政运输网必须至少覆盖该地市附近的16个支局Z58, Z59,Z73和5个县局X1 ,，X5。各县级邮政运输网必须覆盖本县内区级邮车不到达的支局。该地区邮局间公路网分布见表1， 并且县级邮车平均时速为30km/h， 区级邮车的平均时速为65km/h，邮车在各支局卸装邮件耗时5 分钟，在各县局卸装邮件耗时10 分钟。问题 1：以县局X1及其所辖的16个支局Z1, Z2,Z16为研究对象，假设区级第一班次邮车08:00 到达县局X1 ，区级第二班

7、次邮车16:00 从县局 X1 再出发返回地市局D， 若每辆县级邮车最多容纳65袋邮件， 试问最少需要多少辆邮车才能满足该县的邮件运输需求？同时，为提高邮政运输效益，应如何规划邮路和如何安排邮车的运行？（邮件量见表2， 空车率=（邮车最大承运的邮件量（袋 ）-邮车运载的邮件量（袋 ）/邮车最大承运的邮件量（袋 ），单车由于空车率而减少的收入为（空车率*2 元 /km ） ）问题2：采用尽可能少、尽可能短的邮路可以减少邮政部门车辆和人员等的投入，从而显著降低全区邮政运输网的总运行成本。考虑投入车况较好的邮车，通常每条邮路只需要一辆邮车即能满足运载能力要求，试问应如何构建该地区的邮政运输网络（县的

8、划分不能变更）， 请你给出邮路规划和邮车调度方案。请注意邮车的调度必须满足上文中有关该地区的邮政运输流程及时限规定。（每条邮路的运行成本为3 元 /km）问题3：考虑到部分县与县交界地带的支局，其邮件由邻县县局负责运送可能会降低全区的运行成本，带来可观的经济效益。若允许在一定程度上打破行政区域的限制，你能否给出更好的邮路规划和邮车调度方案？（在此同样不必考虑邮车的运载能力的限制，每条邮路的运行成本为3 元 /km）问题4：县局选址的合理与否对构建经济、快速的邮政运输网络起到决定性的作用。假设图2中县局X1,X5均允许迁址到本县内任一支局处，同时原来的县局弱化为普通支局。设想你是该地区网运部门负

9、责人，请你重新为各个县局 选址，陈述你的迁址理由并以书面材料形式提交省局网运处。表1:（详细信息请参照Excel文档：邮局间直达公路里程.xls）邮局i邮局j直达公路里程（km）DZ4250DZ5954DZ6043DZ6122DZ6240DZ6351DZ6551Z72Z7313表2：V支目 邮 局件、Z1Z2Z3Z4Z5Z6Z7Z8Z9Z10Z11Z12Z13Z14Z15Z16寄达局为Z i的邮件量（袋）101569136114131711211211314支局Zi收寄的邮件量（袋）9145109101391596713151016二、基本假设1 .各条路线的路况相差不大，耗费与路程成正比。2

10、 .邮车保持匀速行驶。三、问题1的分析和建模准备1 .分析本问题以一个县（包含县局 X1和16个支局）为研究对象，解决以下两个 问题：（1）在满足该县邮件运输需求的前提条件下，求出最少邮车数量；（2）合理规划各邮车的运行路线，在确保完成邮件运输任务的条件下，使 经济效益最高。以上两个问题可以分成两步来解决，第一步确定最少用多少辆邮车能够按时完成邮件运输任务，第二步对16个支局进行优化分组，使得费用最省。首先考虑最少邮车数量，由题目所给表2中的数据，寄达16个支局的邮件 总数为176袋，从各支局收寄的邮件总数为170袋，每一辆邮车最多容纳65袋 邮件，至少需要176 ft 2.7辆邮车，由于邮车

11、数量n为整数，因此n知卫6,即 6565最少需要3辆邮车。如果3辆邮车在规定的时间内能够完成邮件运输任务，则 3辆车就是邮车数量的最优解。假设3辆邮车可以按时完成任务，则第二步要解决的问题是，将16个支局 分成3组，分别由3辆邮车包干负责邮件送达和收寄，每组（每辆邮车）的起 点和终点都是县局，每个支局都必须有邮车到达，且只需一次，科学地规划邮 车在本组内的行驶路线，使得总费用最小，题目所给由于空车率而减小的收入 为空车率*2元/km,如果空车率变化不大，则损失与总行驶公里数成正比，而 邮车的行驶费用（含耗油量、磨损折旧、维修）通常与行驶公里数成正比，所 以，只要3辆邮车的总行驶里程最小，则行驶

12、成本（费用）费用也是最小，假 如16个支局已经分成了 3组，各组安排一辆邮车，它在本组内的最优行驶路线 相当于找出一条能够到达组内每个支局一次且只需一次，最后回到县局，行驶 里程最短的路线，这个问题相当于旅行售货商（TSP）模型，但是有附加约束条件 （时间约束和载重约束）。安排3辆邮车的最优行驶路线可以作为一个整体优化模型，其目标可以有 以下两点考虑：（1） 3辆邮车的合计行驶里程最少；（2）空车率损失最小。空车率与寄达各支局的邮件量以及从各支局收寄的邮件量有关，在邮车达 到一个支局以后，卸下寄达该支局的邮件，装上需要寄走的邮件，空车率发生 一些变化，因为邮车的负载每天有变化，所以空车率每天都

13、不相同。县局以及各支局之间的距离是相对固定不变的，我们应当尽可能使每一辆 邮车的行驶路线相对固定，避免每天重新做规划，使路线变来变去，万一某一 天某个支局的邮件较多，偶尔超载几袋邮件不至于发生大问题。由此看来，两个目标函数相比较，第一目标是关键，把3辆邮车的总行驶里程最少作为首要目标，而第二目标，即空车率最小可以作为次要目标。设各辆邮车的行驶里程为sk（k =1,2,3）,则目标函数可以写成：3m i n 二 sk（1）约束条件有以下两条：(1)时间约束按照题意，区级(地市局)邮车 8:00达到县局，集中处理1小时(含邮件 的卸装)，县级邮车在9:00出发前往本县支局，因为区级邮车16:00从

14、县局出发 返回，县级邮车完成运输任务返回县局以后，县局还需要集中处理 1小时，所 以县级邮车必须在15:00之前回到县局，可以利用的时间最多为 6小时，即行 车时间加上装卸时间合起来不超过 6小时，如果某一辆邮车的行驶里程为 L, 负责m个支局，则行车时间为L/30小时(2L分钟)，卸装邮件用时5m分钟， 于是该邮车的时间约束可以表示为：2L 5m M 360(2)(2)运载量约束题目规定，每一辆邮车最多装65袋邮件。假设按照行车计划，某一辆邮车 去m个支局，寄达这些支局的邮件量为Pj,支局收寄的邮件量为Qj,则该邮车m从县局出发时的邮件总量为 Z Pj ,达到某个支局以后，卸下Pj袋，装上Q

15、j袋, j 1经过若干次卸和装，到达第n个支局以后，邮车上的邮件量变为 mnE Pj - £ (P-QJ,(n =1,2,，m),在达到最后一个支局后,所有寄达各支局 j 1i 1m的邮件全部卸完，从各支局收寄的邮件全部装上邮车，总装载量变为Z Qi ,在i=1邮车行驶全过程中，限制运载量始终不超过65袋，于是运载量约束可以表示为：1 m£ Pj <65j 1mn' Pj J (P -Qi) £65,(n =1,2,m)j 1iT由以上分析可知，问题1需要解决的问题是：先把16个支局分成3个组， 一辆邮车承包一个组，负责组内各支局邮件的送达和收寄，然

16、后规划各组最优 行驶路线使目标函数最优，分组以及组内行车路线都会影响最后结果，这是一 个求整体最优化的规划问题，它有明确的目标函数和约束条件，但不能把分组 和组内行驶路线隔离起来，即不能孤立地分开处理成两个问题。这相当于有附 加约束条件的多人旅行商问题。为了对16个支局进行科学分组并建立解决问题 1的数学模型，需要做一些 建模前的准备工作，例如求出16个支局和县城共17个节点中任意两个点之间 的最短路、找出该公路网的最小生成树、根据两两节点之间的距离对16个支局 进行聚类分析。2任意两点之间的最短路径在图论中求解最短路的较成熟的方法是Dijkstra 和 Floyd 算法， 其中 Dijkst

17、ra算法适用于指定某个节点为起点，从该点出发到其它任意点的最短路，换另外起点时需要重新编程，而Floyd 算法能够一次性求出任意两点之间的最短路，它是一种通过循环进行逐步比较、动态寻优的方法，可以在Matlab 中用矩阵运算来解决，输入节点的距离矩阵，输出计算结果(最短路矩阵和表示最短路经过哪些节点的路径矩阵)先编写 Flody 算法的子程序(函数)如下：function D,R=floyd(a)n=size(a,1);D=a;for i=1:nfor j=1:n R(i,j)=j;endendfor k=1:nfor i=1:nfor j=1:nif D(i,k)+D(k,j)<D(i

18、,j) D(i,j)=D(i,k)+D(k,j);R(i,j)=R(i,k);endendendendD,R将以上程序以文件名floyd.m 存盘。编写主程序如下：a=0, 27, 44, 17, 11, 27, 42, inf, inf, inf, 20, 25, 21, 21, 18, 27, inf;27, 0, 31, 27, 49, inf,inf,inf,inf,inf,inf,inf,52,21,41,inf,inf;44,31,0,19,inf,27,32,inf,inf,inf,47,inf,inf,inf,50,inf,inf;17,27,19,0,14,inf,inf,i

19、nf,inf,inf,30,inf,inf,inf,31,inf,inf;11,49,inf,14,0,13,20,inf,inf,28,15,inf,inf,inf,15,25,30;27,inf,27,inf,13,0,9,21,inf,26,26,inf,inf,inf,28,29,inf;42,inf,32,inf,20,9,0,13,inf,32,inf,inf,inf,inf,inf,33,inf; inf,inf,inf,inf,inf,21,13,0,19,inf,inf,inf,inf,inf,inf,inf,inf; inf,inf,inf,inf,inf,inf,inf,

20、19,0,11,20,inf,inf,inf,inf,33,21;inf,inf,inf,inf,28,26,32,inf,11,0,10,20,inf,inf,29,14,13;20,inf,47,30,15,26,inf,inf,20,10,0,18,inf,inf,14,9,20;25,inf,inf,inf,inf,inf,inf,inf,inf,20,18,0,23,inf,inf,14,inf;21,52,inf,inf,inf,inf,inf,inf,inf,inf,inf,23,0,27,22,inf,inf;21,21,inf,inf,inf,inf,inf,inf,inf,

21、inf,inf,inf,27,0,inf,inf,inf;18,41,50,31,15,28,inf,inf,inf,29,14,inf,22,inf,0,11,inf;27,inf,inf,inf,25,29,33,inf,33,14,9,14,inf,inf,11,0,9;inf,inf,inf,inf,30,inf,inf,inf,21,13,20,inf,inf,inf,inf,9,0;D,R=floyd(a);程序中的a 是县局 X1 和 16 个支局之间的距离矩阵，运行以上程序，求得最短路矩阵为：X1Z1Z2Z3Z4Z5Z6Z7Z8Z9Z10Z11Z12Z13Z14Z15Z16X1

22、027361711243144403020252121182736Z1270312738515871675747524821415261Z2363101933273245645347615752485663Z3172719014273447493929423838293844Z4113833140132033352515333232152430Z524512727130921372626434545282938Z631583234209013323235475252353342Z7447145473321130193039506565484440Z84067644935373219011203

239305753392526323011010204351241413Z1020474729152635392010018364114918Z11255261423343475031201802346251423Z12214857383245526554433623027223342Z13212152383245526561514146270394857Z14184148291528354834241425223901120Z152752563824293344251491433481109Z1636616344303842402113182342572090程序能够同时

24、求出路径矩阵（最短路经过哪些节点）以能磅夕同M卜求出解径加车：（最短路-经过:哪些;节点），此处省略结果。此处省略结果。3最小生成树最小生成树是网络优化的重要基础，在分析解决各种网络优化问题时能够起到重要作用。将县局 X1以及16个支局(Z1,Z2j,Z16)作为一个网络，求其最小生成树。下面用整数规划法来解决(该方法的原理详见 LINGO 和 Excel在数学建模中的应用第78 页) ，编写 LINGO 程序如下：MODEL:sets:city / 1.17/: u;link( city, city): dist, x;endsetsn = size( city);data:dist =0,

25、27,44,17,11,27,42,800,800,800,20,25,21,21,18,27,80027,0,31,27,49,800,800,800,800,800,800,800,52,21,41,800,80044,31,0,19,800,27,32,800,800,800,47,800,800,800,50,800,800 17,27,19,0,14,800,800,800,800,800,30,800,800,800,31,800,800 11,49,800,14,0,13,20,800,800,28,15,800,800,800,15,25,3027,800,27,800,13,

26、0,9,21,800,26,26,800,800,800,28,29,800 42,800,32,800,20,9,0,13,800,32,800,800,800,800,800,33,800 800,800,800,800,800,21,13,0,19,800,800,800,800,800,800,800,800 800,800,800,800,800,800,800,19,0,11,20,800,800,800,800,33,21 800,800,800,800,28,26,32,800,11,0,10,20,800,800,29,14,1320,800,47,30,15,26,800,

27、800,20,10,0,18,800,800,14,9,2025,800,800,800,800,800,800,800,800,20,18,0,23,800,800,14,800 21,52,800,800,800,800,800,800,800,800,800,23,0,27,22,800,800 21,21,800,800,800,800,800,800,800,800,800,800,27,0,800,800,800 18,41,50,31,15,28,800,800,800,29,14,800,22,800,0,11,80027,800,800,800,25,29,33,800,33

28、,14,9,14,800,800,11,0,9800,800,800,800,30,800,800,800,21,13,20,800,800,800,800,9,0; enddatamin = sum( link: dist * x);U(1)=0;for( link: bin( x);for(city(K)|K#GT#1:sum(city(I)|I#ne#K:x(I,K)=1;for(city( J)| J#gt#1 #and# J #ne# K:u(J)>=u(K)+X(K,J)-(N-2)*(1-X(K,J)+(N-3)*X(J,K);););sum( city( J)| J #G

29、T# 1: x( 1, J) >= 1;for(city(K)|K#gt#1:U(K)>=1;U(K)<=N-1-(N-2)*X(1,K);); end图3县局X1以及16个支局的网络最小生成树运行以上程序，求得一种最小生成树如图3所示，树的总长度为221km,包含 16 条边:X1-Z4, X1-Z12, X1-Z13, Z13-Z1, Z4-Z3, Z3-Z2 , Z4-Z5, Z5-Z6, Z6-Z7, Z4-Z10, Z10-Z9, Z9-Z8, Z10-Z15, Z15-Z16, Z15-Z11, Z15-Z14。需 要注意的是：最小生成树不一定是唯一的。求网络最小

30、生成树的成熟算法有Prim (普里姆)算法和Kruskal (克鲁斯卡尔)算法。下面给出分别 Prim算法和Kruskal算法的matlab程序。(1) Prim算法的matlab程序a=0, 27, 44, 17, 11,27, 42, inf, inf, inf, 20, 25, 21,21, 18, 27, inf;27, 0, 31,27, 49, inf,inf,inf,inf,inf,inf,inf,52,21,41,inf,inf;44,31,0,19,inf,27,32,inf,inf,inf,47,inf,inf,inf,50,inf,inf;17,27,19,0,14,in

31、f,inf,inf,inf,inf,30,inf,inf,inf,31,inf,inf;11,49,inf,14,0,13,20,inf,inf,28,15,inf,inf,inf,15,25,30; 27,inf,27,inf,13,0,9,21,inf,26,26,inf,inf,inf,28,29,inf; 42,inf,32,inf,20,9,0,13,inf,32,inf,inf,inf,inf,inf,33,inf; inf,inf,inf,inf,inf,21,13,0,19,inf,inf,inf,inf,inf,inf,inf,inf; inf,inf,inf,inf,inf

32、,inf,inf,19,0,11,20,inf,inf,inf,inf,33,21; inf,inf,inf,inf,28,26,32,inf,11,0,10,20,inf,inf,29,14,13; 20,inf,47,30,15,26,inf,inf,20,10,0,18,inf,inf,14,9,20; 25,inf,inf,inf,inf,inf,inf,inf,inf,20,18,0,23,inf,inf,14,inf; 21,52,inf,inf,inf,inf,inf,inf,inf,inf,inf,23,0,27,22,inf,inf; 21,21,inf,inf,inf,in

33、f,inf,inf,inf,inf,inf,inf,27,0,inf,inf,inf;18,41,50,31,15,28,inf,inf,inf,29,14,inf,22,inf,0,11,inf; 27,inf,inf,inf,25,29,33,inf,33,14,9,14,inf,inf,11,0,9; inf,inf,inf,inf,30,inf,inf,inf,21,13,20,inf,inf,inf,inf,9,0; T=;e=0;v=1;n=size(a,1);c=2:n;for j=2:nb(1,j-1)=1;b(2,j-1)=j;b(3,j-1)=a(1,j);endwhile

34、 size(T,2)<n-1m,i=min(b(3,:);T(:,size(T,2)+1)=b(:,i);e=e+b(3,i);v=b(2,i);v,t=find(c=b(2,i);c(t)= ;b(:,i)= ;for j=1:length(c)d=a(v,b(2,j);if d<b(3,j)b(1,j)=v; b(3,j)=d;endendendT,e(2) Kruskal 算法的 matlab 程序矩阵a与前面相同，此处省略k=0;n=size(a,1);for i=1:n-1for j=i+1:nif a(i,j)>0 & a(i,j)<800k=k+1

35、;b(1,k)=i;b(2,k)=j;b(3,k)=a(i,j);endendendB,i=sortrows(b',3);B=B'm=size(b,2);t=1:n;k=0;T= ;c=0;for i=1:mif t(B(1,i)=t(B(2,i)k=k+1; T(k,1:2)=B(1:2,i);c=c+B(3,i);tmin=min(t(B(1,i),t(B(2,i);tmax=max(t(B(1,i),t(B(2,i);for j=1:nif t(j)=tmaxt(j)=tmin;endendendif k=n-1break;endendT,c以上程序运行结果与LINGO

36、的结果基本相同(见图3) 。4聚类分析聚类分析通过分析数据，根据它们之间的相似关系，合理地划分数据集合，使同一类别内的个体差别尽量小，而不同类别上的个体差别尽量大。聚类分析是一种探索性的分析，在分类过程中，人们不必事先给出一个分类标准，也不 必确定分成几类，聚类分析能够从样本数据出发，按照它们在性质上的的相近 程度在没有先验知识的情况下自动进行分类。聚类分析的方法中有一种称为层次聚类分析方法，它使具有共同特点的样 本聚齐在一起，根据观测值或变量之间的亲疏程度，将最相似的对象结合在一 起，以逐次聚合（分解）的方式将观测值分类。又分成两种：（1）自顶向下，开始时所有对象为一类，然后逐步分裂，直至每

37、个对象单 独为一类。（2）自底向上，开始时每个对象为一类，逐次合并相近的对象，直至所有 样本都聚为一类。分类的重要依据是对象之间的距离，这里所说的距离是广义上的距离概念， 不是单纯的几何意义上的距离。前面我们求出了任意两个节点之间的最短路， 不妨就把节点之间的几何距离作为分类的主要依据，对它们进行自底向上的聚 类分析。开始时类的总数等于对象数目，然后将相互之间距离最近的两个（或 几个）对象归为一类，逐步减少类别的总数，直至达到预设的类别数或较理想 的状态。判别聚类效果是否优的标准是同一类内的差别（平均距离）尽可能小,而不同类之间差别（指标）尽可能大。riFnrli口考tke匕Linkf 巳-

38、(INi thin Grouj:)Res:aled rictance Cluster ComL incCASELabelNum2L0 ?L5 蒲 以 6 ill311 ZS £12 Z526 乳23 Z72L ZL32213-图4根据距离对16个支局聚类分析的结果15一十5H可以用统计分析软件SPSS来进行聚类分析，将最短路矩阵输入 SPSS统计分析软件，执行 AnalyzeYlassifyTierarchical Cluster （层次聚类分析），在 Cluster Method （聚类方法）选项中选择 Within-group linkage （组内连接法，即 同一类中所有项之间

39、的平均距离最小），点击“OK”，得到结果如图4所示。从结果分析，支局10,15,9,16,14,11,8,1怨第一组（排队越靠前，关系越紧 密），5,6,4,3,7是第二组，1,13,2是第三组。因为这种分组只考虑了支局之间的 距离，没有考虑邮车装载量约束，如第一组含8个支局，邮件的总量为97袋，超过最大装载量65,所以聚类结果只能供参考而不能作为邮车规划的依据。为了在分类的同时考虑邮件装载量约束，可以建立规划模型对16个支局进 行分类（分组）。用i =1,2，,16表示16个支局，k =1,2,3表示3个组，Pi表示 寄达支局Zi的邮件量，Qi表示从支局Zi收寄的邮件量，用0-1型决策变量X

40、ik 表示支局i,是否分在第k组，Xik =1表示支局i分在第k组，Xik =0表示否。每两个支局之间均存在最短路（有些支局之间没有直接通路，但存在经过其它 支局的间接路径），用Cij表示支局i与支局j之间的最短路。约束条件如下:（1）每个支局必须分一次，且只能分到一组（2）每个组最多8个支局，最少3个支局（该条件并非必须）65袋。1516Lk = £ £ Cj Xik，Xjk ,组 i W j iL,优化分组的目标是使总平均 mk（3）各组寄达和收寄的邮件总量都不超过第k组内两两支局之间最短路经的总和为16内支局数量为mk =£ Xik ,组内平均距离为i 1距

41、离达到最小。综上所述，建立优化分组的规划模型如下:.:Lk min km mk3X Xik =1, i =1,2，16 k=i16mk =£ Xik , k =1,2,3 I3 <mk <8 , k =1,2,316«£ Pi 凡 W65,k =1,2,3 iT16Q Qi -Xik E65,k =1,2,3 iT15 16Lk =££ Cij Xik -Xjk ,k =1,2,3 i3 j>Xik =0 或 1以上规划模型可以用LINGO 求解，编写程序如下：MODEL:SETS:ZHIJU/1.16/: P,Q;GROUP

42、/1.3/:L,M,YJ,YD;FL( ZHIJU, GROUP): X;LINKS(ZHIJU,ZHIJU)|&2#GT#&1:C;ENDSETSDATA:P=10,15,6,9,13,6,11,4,13,17,11,2,11,21,13,14;Q=9,14,5,10,9,10,13,9,15,9,6,7,13,15,10,16;C=31 27 38 51 58 71 67 57 47 52 48 21 41 52 6119 33 27 32 45 64 53 47 61 57 52 48 56 6314 27 34 47 49 39 29 42 38 38 29 38 44

43、13 20 33 35 25 15 33 32 32 15 24 309 21 37 26 26 43 45 45 28 29 3813 32 32 35 47 52 52 35 33 4219 30 39 50 65 65 48 44 4011 20 31 54 61 34 25 2110 20 43 51 24 14 1318 36 41 14 9 1823 46 25 14 2327 22 33 4239 48 5711 209;ENDDATAFOR( FL : BIN( X);FOR(ZHIJU(I): SUM(GROUP(K): X(I,K) = 1);FOR(GROUP(K):M(

44、K)=SUM(ZHIJU(I):X(I,K);FOR(GROUP:M<=8); FOR(GROUP:M>=3);FOR(GROUP(K):YJ(K)=SUM(ZHIJU(I):X(I,K)*P(I);FOR(GROUP(K):YD(K)=SUM(ZHIJU(I):X(I,K)*Q(I);FOR(GROUP:YJ<=65); FOR(GROUP:YD<=65);FOR(GROUP(K):L(K)=SUM(LINKS(I,J):C(I,J)*X(I,K)*X(J,K);MIN=SUM(GROUP:L/M);END运行以上程序，得到结果如下：第 1 组：2,3,4,5,6,7

45、,总里程 387km,总邮件 60,61。第 2 组：1,11,12,13,14,总里程 344km,总邮件 55,50。第 3 组：8,9,10,15,16,总里程 150km,总邮件 61,59。以上分组可以作为规划邮车路线的参考。四、问题1的模型1 .组内路径优化模型虽然邮路并不限定是环形邮路，可以是辐射形或混合形，对于少数比较孤立的支局，也许只能去了以后再原路返回（根据具体情况具体分析），但是，因为距离矩阵中两点之间的距离取最短路，若两点之间没有直接的通路，该两点 之间的距离不表示成无穷大，而是取最短路，故本题的邮政网络可以看成是一 个完全图（即任意一对顶点都有一条边相连），于是，形式

46、上的环形路线实际上 有可能带有辐射形，个别点有可能不止经过一次。假如已经把支局分了 3组，每一辆邮车负责一个组，则余下的问题是规划 邮车行驶路线，从县局出发，逐次行进到达一个一个支局，每个支局都到一次 且仅需一次，最后回到县局，整个旅程是一个回路（圈），合理安排行驶路线， 使总里程最短，这类似于网络优化中的旅行商（TSP）问题，但是附加了额外的约束条件。可以参考一些解决 TSP问题的方法求解。我们另辟途径，把该问题转换成以县局为起点和终点，对组内支局优化排 序，合理安排装卸点的顺序，使行驶总里程最短的规划问题。邮车行走路线分成m+1个步骤，第一步从县局出发到某个支局，该支局即 排在第一位，第二

47、步从该支局出发到另一个支局 （这个支局排在第二位），依次 类推，直至第m步到达组内最后一个支局，然后第m+1步从最后一个支局返回 县局。行驶路线不同（即支局的排序不同），全程的总路程也不同，总路程最小 的排序就是邮车行进的最佳路线，即我们要寻找的最优解。引入0-1型决策变量Xnj,下标n表示邮车行走的步数，下标j表示到达哪 一个支局，Xnj =1表示邮车第n个目标（装卸点）是支局j, Xnj =0表示否。用Cij表示支局i与支局j之间的最短路。约束条件有以下 4条:m(1)每一步到达一个支局，即 £ Xnj =1,n =1,2,，m。j 1 m(2)每一个支局必须到一次且只需一次，即

48、 Z Xnj =1, j =1,2,，m。n 1必须分一次，且只能分到一组。(3)在邮车行进的任何路段上，装载的邮件不超过65袋。(4)行车时间不超过6小时( 360分钟)，若行驶总里程为L,在m个支局 进行装卸，则行车时间为L/30小时(2L分钟)，卸装邮件用时5m分钟，于是 该邮车的时间约束为：2L +5m <360o设寄达组内各支局的邮件量为 Pj,各支局收寄的邮件量为 Qj,则邮车从县 mm局出发时的邮件总量为 W0 =£ Pj ,达到第一个支局以后，卸下 Z Pj，X1j袋， j：j wmm装上Q Qj ,X1j袋，从该支局出发时的装载量为 W1 =W0 -Z (Pj

49、 -Qj)，X1j。由 j 1j 1于m个X1j中实际只有一个等于1 (其余m-1个都等于0),所以计算式中虽然 有求和表达式，但是实际上装卸的只是邮车所到达支局计划内应该卸和装的邮 件，依此类推，从第n个支局出发时的装载量的递推关系为mmmnWn =Wn。-£ (Pj -Qj)人=£ Pj(Pj -Qj) Z Xqj 0 从最后一个支局出发j 1j d jdq=1m返回县局的路上，邮车的装载量变为 Wm=£Qj ,综上所述，各段路程上邮车j 1装载量是变化的，计算公式为：-mw0 = £ Hj 1(5) mnWn =W -V (Pj -Qj) '

50、; Xqj j=1qw限制运载量始终不超过65袋，即皿W65,i =0,1,2,，m。在邮车从一个点到另一个点的途中，若装载量为四(单位：袋)，该段路程长度为Lj (单位：km),则题目定义空车率为 吃=(65-Wj)/65 = 1-"，由65空车引起的损失费为2Nj L =(2-m)L ,与行驶里程成正比。65目标函数可以取两种：(1)总路程最小；(2)空车损失最小。由于空车损失与行驶里程成正比，所以优化的最基本目标是优化到达各支局的先后次序使行驶总里程最小。首先要根据决策变量的0-1值，计算出邮车从一个支局到另一个支局所走过的路程，假设在第 n步邮车达到支局i,在第 n+1步达到

51、支局j,即Xni和Xn4j同时等于1,则走过的里程为Cij，Xni，Xn刊j, 式中Cij是支局之间的最短路距离矩阵。用lj表示县局到各支局的最短路距离，m则邮车从县局出发到第一个点的行驶里程为 Z ij .Xij ,从第一个装卸点到最后j 1mJ m m一个装卸点（共有 m-1段）行驶的总里程为ZZZ Cij ,XnXn书,j ,从最后一 nJ i 4 j=1m个点返回县局的行驶里程为£ l j 'Xmj。综上所述，以总里程最短作为目标j w函数，当总路程最短时，自然行车时间也是最短，求出目标函数的最小值以后 就可以判断时间约束条件是否能够得到满足，故模型中暂时不用考虑时间

52、约束由此建立如下数学模型： mm-1 m mmmin L = " lj X1j Ci j Xni Xn 1,j 1 j Xm jj 1n 3 i 3 j 3j 1m m(6)X Xnj =1,n=1,2i ,m j苴ms.t.辔 Xnj =1 , j =1,2,，m n =1w M65 ,i =0,1,2，mXnj =0 或 1式中装载量Wi由（5）式来计算。以上规划可以用LINGO来求解，对于第一组（支局2,3,4,5,6,70 ,编写程序 如下：MODEL:SETS:STATION/2,3,4,5,6,7/: JL,P,Q;ORDER/1.6/:W;LINE( ORDER, ST

53、ATION): X;LINKS(STATION,STATION):C;ENDSETSDATA:JL=36,17,11,24,31,44;P=15,6,9,13,6,11;Q=14,5,10,9,10,13;C=0,19,33,27,32,4519,0,14,27,34,4733,14,0,13,20,3327,27,13,0,9,2132,34,20,9,0,1345,47,33,21,13,0;ENDDATAFOR( LINE : BIN( X);M=SIZE(STATION);FOR(STATION(I): SUM(ORDER(N): X(N,I) = 1);FOR(ORDER(N):SUM(STATION(I):X(N,I)=1);W0=SUM(STATION:P);W(1)=W0-SUM(STATION(J):(P(J)-Q(J)*X(1,J);FOR(ORDER(N)|N#GE#2:W(N)=W(N-1)-SUM(STATION(J):(P(J)-Q(J)* X(N,J);FOR(ORDER(N):W(N)<=65);L=SUM(STATION(I):X(1,I)*JL(I)+X(6,I)*JL(I);L1=SUM(ORDER(N)|N#L