立体几何大题20道

1、立体几何大题20道1、(17年浙江)如图，已知四棱锥P-ABCD , APAD是以AD为斜边的等腰直角三角形，BC / AD , CD丄AD ,PC=AD=2DC=2CB,E为PD的中点.(I)证明：CE /平面PAB; (II)求直线 CE与平面PBC所成角的正弦值2、(17新课标3)如图，四面体 ABCD中， ABC是正三角形，AD=CD . ( 1)证明：AC丄BD； ( 2)已知 ACD是直 角三角形，AB=BD .若E为棱BD上与D不重合的点，且 AE丄EC,求四面体 ABCE与四面体ACDE的体积比.3、( 17新课标2)如图，四棱锥 P ABCD中，侧面PAD为等边三角形且垂直于

2、底 ABCD,1AB BC -AD, BAD ABC 90 . (1)证明：直线 BC/平面 PAD；(2)若 PCD的面积为2j7，求四棱锥P ABCD的体积.8（2）若PA=PD=AB=DC, aPD 90°，且四棱锥P-ABCD的体积为-，求该四棱锥的侧面积.3c5、（ 17年山东）由四棱柱 ABCD-AiBiCiDi截去三棱锥 Ci- B1CD1后得到的几何体如图所示，四边形ABCD为正方形，0为AC与BD的交点,E为AD的中点,AiE 平面ABCD,(I)证明：A0 /平面 BiCDi;（n）设M是0D的中点，证明：平面AiEM 平面BiCDi.6、（ i7年北京）如图，在

3、三棱锥P 识BC 中，PA 丄 AB, PA丄 BC, AB丄 BC, PA=AB=BC=2 , D 为线段 AC 的中点,E为线段PC上一点.（I）求证:PA丄BD ;（n ）求证：平面 BDE丄平面PAC;（川）当PA/平面BDE时，求三棱锥 E -BCD的体积.7、（ 16年北京）如图，在四棱锥 P-ABCD中, pc丄平面ABCD AB / DC, DC AC(I)求证：DC 平面PAC ; (II )求证：平面PAB 平面PAC .(III)设点E为AB的中点，在棱 PB上是否存在点F,使得PA/平面CEF ?说明理由8、(16年山东)在如图所示的几何体中，D是AC的中点，EF/ D

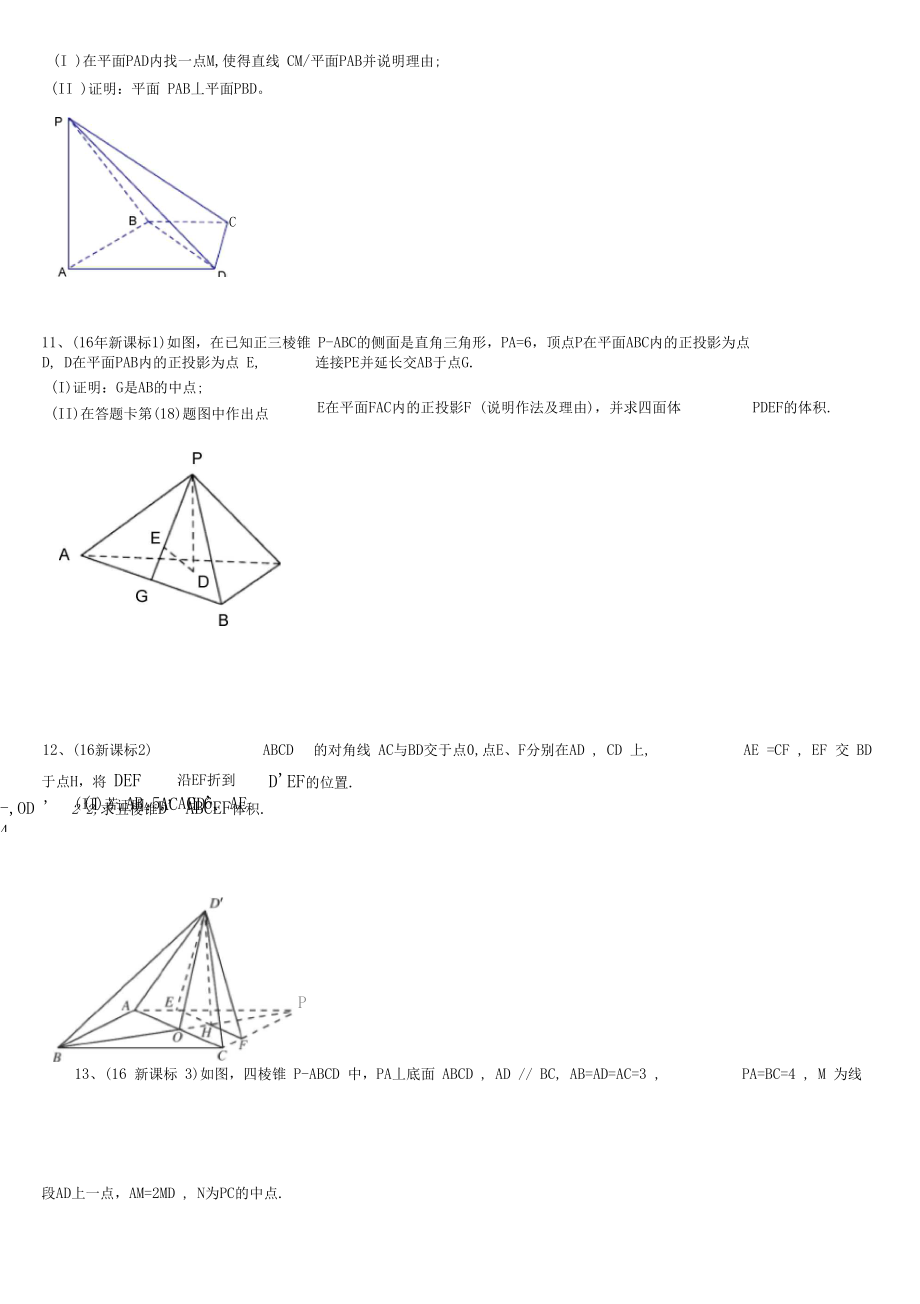
4、B.(I )已知 AB=BC AE=EC求证：AC丄 FB;(II )已知G,H分别是EC和FB的中点.求证：GH/平面 ABC.B9、( 16年上海)将边长为1的正方形AAiOiO (及其内部)绕 001旋转一周形成圆柱,如图，AC长为影长为3,其中B1与C在平面AA1010的同侧.求圆柱的体积与侧面积;求异面直线OiBi与0C所成的角的大小.2 AD。W|10、如图，在四棱锥 P-ABCD中，PA丄 CD, AD/ BC, / ADC=Z PAB=90 , BC CD(I )在平面PAD内找一点M,使得直线 CM/平面PAB并说明理由;(II )证明：平面 PAB丄平面PBD。C11、(1

5、6年新课标1)如图，在已知正三棱锥 P-ABC的侧面是直角三角形，PA=6，顶点P在平面ABC内的正投影为点D, D在平面PAB内的正投影为点 E,连接PE并延长交AB于点G.(I)证明：G是AB的中点;(II)在答题卡第(18)题图中作出点E在平面FAC内的正投影F (说明作法及理由)，并求四面体PDEF的体积.12、(16新课标2)ABCD的对角线 AC与BD交于点0,点E、F分别在AD , CD 上,AE =CF , EF 交 BD于点H，将 DEF沿EF折到D'EF的位置.(I )证明：AC HD'.(II)若 AB 5, AC 6, AE-,OD '22,求五

6、棱锥D' ABCEF体积.4P13、(16 新课标 3)如图，四棱锥 P-ABCD 中，PA丄底面 ABCD , AD / BC, AB=AD=AC=3 ,PA=BC=4 , M 为线段AD上一点，AM=2MD , N为PC的中点.(I)证明MN /平面PAB;(II )求四面体N-BCM的体积.14、(2013陕西，18, 12分)如图，四棱柱ABCD-A1B1C1D1的底面ABCD是正方形，0是底面中心，A1O丄底面ABCD, AB= AA1 =近.(1)证明：平面A1BD /平面CD1B1；求三棱柱ABD-A1B1D1的体积.甘q15、(2016 宁夏银川二模，18, 12 分)

7、如图 1,在直角梯形 ABCD 中，/ ADC= 90°, CD/ AB, AD= CD1=2AB= 2,点E为AC中点.将 ADC沿AC折起，使平面 ADC丄平面ABC，得到几何体D-ABC，女口图2所示.(1)在CD上找一点F，使AD/平面EFB;求点C到平面ABD的距离.B16、(2015 山东，18, 12分，中)如图，三棱台DEF-ABC中，AB= 2DE, G, H分别为AC , BC的中点.(1)求证：BD /平面FGH ;求证：平面BCD丄平面EGH.17、（2014 课标 I, 19, 12 分,中）如图，三棱柱ABC-A1B1C1中，侧面BB1C1C为菱形，BQ的

8、中点为0,且AO丄平面BB1C1C.（1）证明:B1C 丄 AB;若 AC丄 AB1 , / CBB1 = 60°,BC= 1,求三棱柱 ABC-A1B1C1的高.18、（2014辽宁，19, 12分）如图， ABC和 BCD所在平面互相垂直，且/ DBC= 120°, E, F, G 分别为 AC, DC, AD 的中点.（1）求证：EF丄平面BCG ;AB= BC= BD = 2,/ ABC=cBD的交点，BE丄平面ABCD.19、（2015课标I , 18, 12分）如图，四边形 ABCD为菱形,证明：平面AEC丄平面BED;(2)若/ ABC= 120°, AE丄EC,三棱锥E-ACD的体积为晋，求该三棱锥的侧面积.20、(2016江苏扬州二模，16, 14分)如图1,在边长为4的菱形ABCD中，/