机械能守恒计算

1、 机械能守恒计算1. 如图所示,ABCDO是处于竖直平面内的光滑轨道,AB是半径为R=15m的圆周轨道,CDO是直径为15m的半圆轨道.AB轨道和CDO轨道通过极短的水平轨道(长度忽略不计)平滑连接.半径OA处于水平位置,直径OC处于竖直位置.一个小球P从A点的正上方高H处自由落下,从A点进入竖直平面内的轨道运动(小球经过A点时无机械能损失).当小球通过CDO轨道最低点C时对轨道的压力等于其重力的倍,取g为10m/s2.(1)试求高度H的大小？(2)试讨论此球能否到达CDO轨道的最高点O,并说明理由？(3)求小球沿轨道运动后经多长时间再次落回轨道上？PAOHCDB 2. 如图所示,一位质量m=

2、60kg参加“挑战极限”的业余选手,要越过一宽度为s=2.5m的水沟,跃上高为H=2.0m的平台,采用的方法是:人手握一根长L=3.25m的轻质弹性杆一端,从A点由静止开始匀加速助跑,至B点时,杆另一端抵在O点的阻挡物上,接着杆发生形变、同时脚蹬地,人被弹起,离地时重心高h=0.8m,到达最高点时杆处于竖直,人的重心在杆的顶端.运动过程中空气阻力可忽略不计.(取g=10m/s2)(1)第一次试跳,人恰能到达最高点,则人在B点离开地面时的速度v1是多少？(2)第二次试跳,人在最高点放开杆水平飞出,恰好趴落到平台边缘,则人在最高点飞出时速度v2至少多大？(3)设在第二次试跳中,人跑到B点时速度大小

3、为vB=8m/s,求人在B点蹬地弹起瞬间,至少应做多少功？OHABs3. 如图所示，一半径R=0.2m的水平圆盘绕过圆心的竖直轴转动，圆盘边缘有一质量m=1.0kg的小滑块。当圆盘转动的角速度达到某一数值时，滑块从圆盘边缘滑落，经光滑的过渡圆管（图中圆管未画出）进入轨道ABC。已知AB段为光滑的弧形轨道，A点离B点所在水平面的高度h=1.2m ；BC斜面与AB轨道对接，倾角为37°，滑块与圆盘及BC斜面间的动摩擦因数均=0.5，滑块在运动过程中始终未脱离轨道，不计在过渡圆管处和B点的机械能损失, 最大静摩擦力近似等于滑动摩擦力，取g=10m/s2，sin37°=0.6，co

4、s37°=0.8（1）当圆盘的角速度多大时，滑块从圆盘上滑落？（2）若取圆盘所在平面为零势能面，求滑块到达B点时的机械能。（3）从滑块到达B点时起，经0.6s正好通过C点，求BC之间的距离。4. 小球A用不可伸长的细绳悬于O点,在O点的正下方有一固定的钉子B,OB=d,初始时小球A与O同水平面无初速度释放,绳长为L,为使小球能绕B点做完整的圆周运动,如图所示.试求d的取值范围.DdLOmBCA5. 如图所示,A物体用板托着,位于离地h=1.0m处,轻质细绳通过光滑定滑轮与A、B相连,绳子处于绷直状态,已知A物体质量M=1.5,B物体质量m=1.0kg,现将板抽走,A将拉动B上升,设A

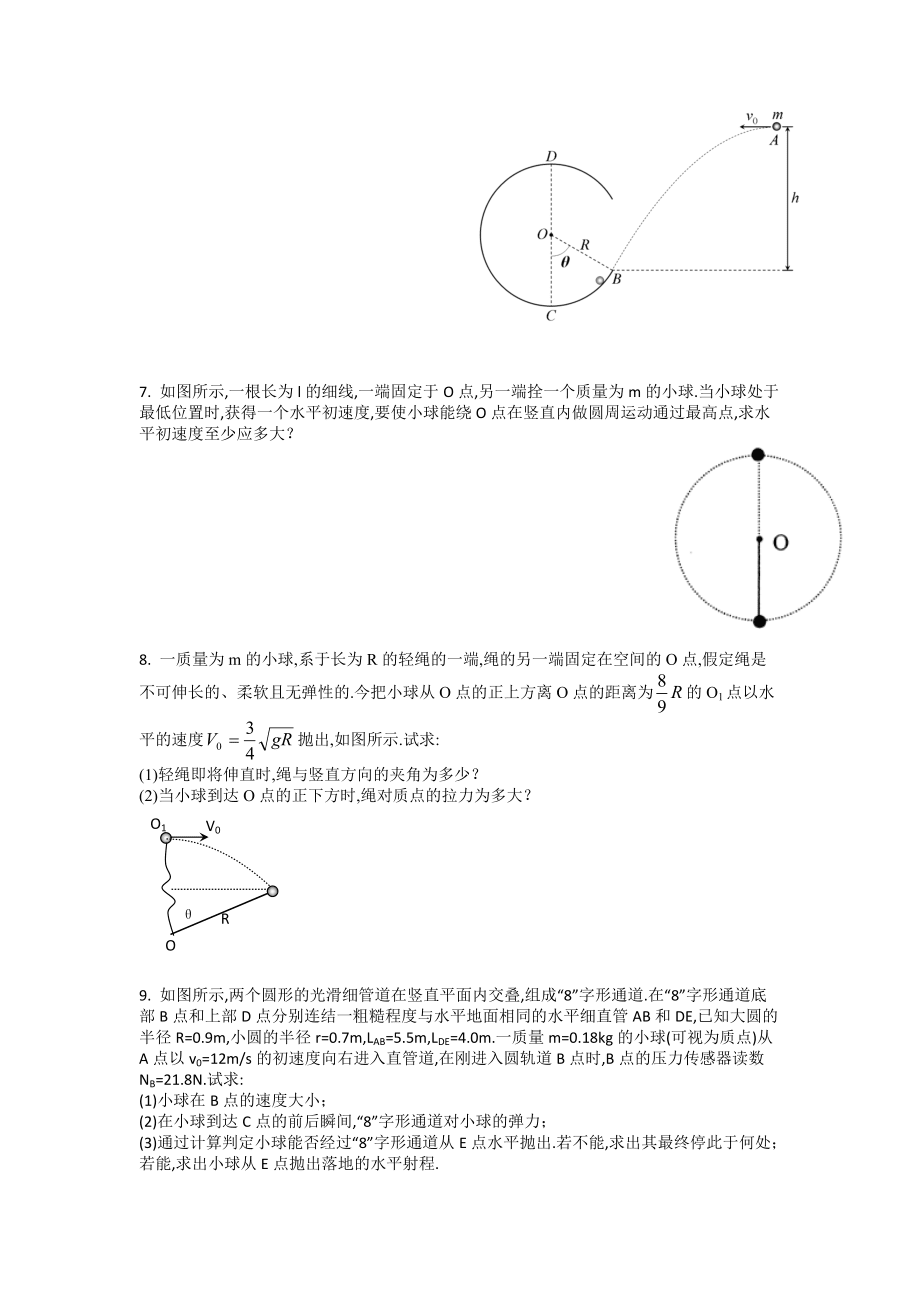
5、与地面碰后不反弹,B上升过程中不会碰到定滑轮,问:B物体在上升过程中离地的最大高度为多大？取g=10m/s2.6. 如图所示,一个半径R=1.0m的圆弧形光滑轨道固定在竖直平面内,轨道的一个端点B和圆心O的连线与竖直方向夹角=60°,C为轨道最低点,D为轨道最高点.一个质量m=0.50kg的小球（视为质点）从空中A点以v0=4.0m/s的速度水平抛出,恰好从轨道的B端沿切线方向进入轨道.重力加速度g取10m/s2.试求:小球抛出点A距圆弧轨道B端的高度h.小球经过轨道最低点C时对轨道的压力FC.小球能否到达轨道最高点D？若能到达,试求对D点的压力FD.若不能到达,试说明理由.7. 如

6、图所示,一根长为l的细线,一端固定于O点,另一端拴一个质量为m的小球.当小球处于最低位置时,获得一个水平初速度,要使小球能绕O点在竖直内做圆周运动通过最高点,求水平初速度至少应多大？8. 一质量为m的小球,系于长为R的轻绳的一端,绳的另一端固定在空间的O点,假定绳是不可伸长的、柔软且无弹性的.今把小球从O点的正上方离O点的距离为的O1点以水平的速度抛出,如图所示.试求:(1)轻绳即将伸直时,绳与竖直方向的夹角为多少？(2)当小球到达O点的正下方时,绳对质点的拉力为多大？V0O1RO9. 如图所示,两个圆形的光滑细管道在竖直平面内交叠,组成“8”字形通道.在“8”字形通道底部B点和上部D点分别连

7、结一粗糙程度与水平地面相同的水平细直管AB和DE,已知大圆的半径R=0.9m,小圆的半径r=0.7m,LAB=5.5m,LDE=4.0m.一质量m=0.18kg的小球(可视为质点)从A点以v0=12m/s的初速度向右进入直管道,在刚进入圆轨道B点时,B点的压力传感器读数NB=21.8N.试求:(1)小球在B点的速度大小；(2)在小球到达C点的前后瞬间,“8”字形通道对小球的弹力；(3)通过计算判定小球能否经过“8”字形通道从E点水平抛出.若不能,求出其最终停此于何处；若能,求出小球从E点抛出落地的水平射程.ABCDEFRrv010. 如图所示,半径R=0.8m的光滑1/4圆弧轨道固定在光滑水平

8、上,轨道上方的A点有一个可视为质点的质量m=1kg的小物块.小物块由静止开始下落后打在圆弧轨道上的B点但未反弹,在该瞬间碰撞过程中,小物块沿半径方向的分速度即刻减为零,而沿切线方向的分速度不变,此后小物块将沿着圆弧轨道滑下.已知A点与轨道的圆心O的连线长也为R,且AO连线与水平方向的夹角为30°,C点为圆弧轨道的末端,紧靠C点有一质量M=3kg的长木板,木板的上表面与圆弧轨道末端的切线相平,小物块与木板间的动摩擦因数,g取10m/s2.求:(1)小物块刚到达B点时的速度；(2)小物块沿圆弧轨道到达C点时对轨道压力FC的大小；(3)木板长度L至少为多大时小物块才不会滑出长木板？11.

9、ACBLL如图所示,物块A的质量为M,物块B、C的质量都是m,并都可看作质点,且mM2m.三物块用细线通过滑轮连接,物块B与物块C的距离和物块C到地面的距离都是L.现将物块A下方的细线剪断,若物块A距滑轮足够远且不计一切阻力.求:(1)物块A上升时的最大速度；(2)物块A上升的最大高度.12. 如图是为了检验某种防护罩承受冲击能力的装置,M为半径为、固定于竖直平面内的光滑圆弧轨道,轨道上端切线水平,N为待检验的固定曲面,该曲面在竖直面内的截面为半径的圆弧,圆弧下端切线水平且圆心恰好位于M轨道的上端点,M的下端相切处置放竖直向上的弹簧枪,可发射速度不同的质量的小钢珠,假设某次发射的钢珠沿轨道恰好

10、能经过M的上端点,水平飞出后落到N的某一点上,取,求:(1)发射该钢珠前,弹簧的弹性势能多大？(2)钢珠落到圆弧上时的速度大小是多少？(结果保留两位有效数字)13. 如图所示轻杆长1m,其两端各连接质量为1kg的小球,杆可绕距B端0.2m处的轴O在竖直平面内转动,轻杆由水平从静止转至竖直方向,A球在最低点的速度为4m/s.求:（1）A球此时对杆的作用力大小及方向（2）B球此时对杆的作用力大小及方向OAB14. 如图所示,一很长的、不可伸长的柔软轻绳跨过光滑定滑轮,绳两端各系一小球a和b.a球质量为2m,静置于地面；b球质量为3m,用手托住,高度为h,此时轻绳刚好拉紧.从静止开始释放b后,求a可

11、能达到的最大高度.15. 滑板运动已成为青少年所喜爱的一种体育运动,如图所示,某同学正在进行滑板运动.图中AB段路面是水平的,BCD是一段半径R=20m的拱起的圆弧路面,圆弧的最高点C比AB段路面高出h=1.25m.已知人与滑板的总质量为M=60kg.该同学自A点由静止开始运动,在AB路段他单腿用力蹬地,到达B点前停止蹬地,然后冲上圆弧路段,结果到达C点时恰好对地面压力为零,不计滑板与各路段之间的摩擦力及经过B点时的能量损失(g取10m/s2).求:(1)该同学到达C点时的速度.(2)该同学在AB段所做的功.16. 如图所示,质量m=2kg的小球以初速度V0沿光滑的水平面飞出后,恰好无碰撞地进

12、入光滑的圆弧轨道,其中圆弧AB对应的圆心角,圆半径R=0.5m.若小球离开桌面运动到A点所用时间.（g=10m/s2）（1）求小球沿水平面飞出的初速度V0的大小？（2）到达B点时,求小球此时对圆弧的压力N1大小？（3）小球是否能从最高点C飞出圆弧轨道,并说明原因.17. 水平传送带距地面高h=0.8m,B、C为光滑圆弧的两端点,其连线水平.圆弧半径R=1.0m,圆弧对应圆心角=106°,斜面CD与圆弧相切与C点.质量为m=1kg的小物块轻轻放在水平匀速运动的传送带上的P点,随传送带运动到A点后水平抛出,物块恰好无碰撞的沿圆弧切线从B点进入圆孤轨道下滑.且物块离开C点恰能无碰撞的沿固定

13、斜面向上运动,经0.8s恰到达D点,物块与斜面间的滑动摩擦因数为（g=10m/s2,sin37°=0.6,cos37°=0.8）试求:（1）小物块离开A点的水平初速度v1（2）小物块经过最低点O点时对轨道的压力（3）斜面上CD间的距离.18. 如图所示,有一长为L的细线,细线的一端固定在O点,另一端拴一质量为m的小球,现使小球恰好能在竖直面内做完整的圆周运动.已知水平地面上的C点位于O点正下方,且到O点的距离为1.9L.不计空气阻力.求:(1)小球通过最高点A时的速度vA；(2)小球通过最低点B时,细线对小球的拉力T；(3)若小球运动到最低点B时细线恰好断裂,小球落地点到C

14、点的距离.19. 如图所示,位于竖直平面内的光滑轨道,由一段斜的直轨道和与之相切的圆形轨道连接而成,圆形轨道的半径为R.一质量为m的小物块从斜轨道上某处由静止开始下滑,然后沿圆形轨道运动.要求物块能通过圆形轨道最高点,且在该最高点与轨道间的压力不能超过5mg(g为重力加速度).求物块初始位置相对于圆形轨道底部的高度h的取值范围.20. 如图所示,光滑曲面轨道置于高度为H=1.8m的平台上,其末端切线水平.另有一长木板两端分别搁在轨道末端点和水平地面间,构成倾角为=37°的斜面,整个装置固定在竖直平面内.一个可视作质点的质量为m=0.1kg的小球,从光滑曲面上由静止开始下滑(不计空气阻

15、力,g取10m/s2,sin37°=0.6,cos37°=0.8)(1)若小球下滑后做平抛运动正好击中木板的末端,则释放小球的高度h为多大？(2)试推导小球下滑后做平抛运动第一次撞击木板时的动能与它下滑高度h的关系表达式.21. 如图所示,一水平圆盘绕过圆心的竖直轴转动,圆盘边缘有一质量m=1.0kg的小滑块.当圆盘转动的角速度达到某一数值时,滑块从圆盘边缘滑落,经光滑的过渡圆管进入轨道ABC.已知AB段斜面倾角为530,BC段斜面倾角为370,滑块与圆盘及斜面间的动摩擦因数均为,A点离B点所在水平面的高度.滑块在运动过程中始终未脱离轨道,不计在过渡圆管处和B点的机械能损失

16、,最大静摩擦力近似等于滑动摩擦力,取,.(1)若圆盘半径为R,当圆盘的角速度多大时,滑块从圆盘上滑落？(2)若取圆盘所在平面为零势能面,求滑块到达B点时的机械能.(3)从滑块到达B点时起,经0.6s正好通过C点,求BC之间的距离.22. 如图所示,小球从光滑的圆弧轨道下滑至水平轨道末端时,光电装置被触动,控制电路会使转筒立刻以某一角速度匀速连续转动起来.转筒的底面半径为R,已知轨道末端与转筒上部相平,与转筒的转距离为L,且与转筒侧壁上的小孔的高度差为h；开始时转筒静止,且小孔正对着轨道方向.现让一小；h；开始时转筒静止，且小孔正对着h球从圆弧轨道上的某处无初速滑下,若正好能钻入转筒的小孔(小孔

17、比小球略大,小球视为质点,不计空气阻力,重力加速度为g),求:(1)小球从圆弧轨道上释放时的高度H；(2)转筒转筒的角速度.23. 如图所示，圆管构成的半圆形轨道竖直固定在水平地面上，轨道半径为R，MN为直径且与水平面垂直，直径略小于圆管内径的小球A以某一速度冲进轨道，到达半圆轨道最高点M时与静止于该处的质量与A相同的小球B发生碰撞，碰后两球粘在一起飞出轨道，落地点距N为2R。重力加速度为g，忽略圆管内径，空气阻力及各处摩擦均不计，求（1）粘合后的两球从飞出轨道到落地的时间t；（2）小球A冲进轨道时速度v的大小。24. 如图所示，长度为l的轻绳上端固定在O点，下端系一质量为m的小球（小球的大小

18、可以忽略）。（1）在水平拉力F的作用下，轻绳与竖直方向的夹角为，小球保持静止，画出此时小球的受力图，并求力F的大小。（2）由图示位置无初速度释放小球，求当小球通过最低点时的速度大小及轻绳对小球的拉力。不计空气阻力。25. 某校物理兴趣小组决定举行遥控赛车比赛。比赛路径如图所示，赛车从起点A出发，沿水平直线轨道运动L后，由B点进入半径为R的光滑竖直圆轨道，离开竖直圆轨道后继续在光滑平直轨道上运动到C点，并能越过壕沟。已知赛车质量m=0.1kg，通电后以额定功率P=1.5w工作，进入竖直轨道前受到阻力恒为0.3N，随后在运动中受到的阻力均可不记。图中L=10.00m，R=0.32m，h=1.25m

19、，S=1.50m。问：要使赛车完成比赛，电动机至少工作多长时间？（取g=10 ） 26. 长为L的轻绳，一端系一质量为M的小球，一端固定于O点，在O点正下方距O点H处有一枚钉子C，现将绳拉至水平位置，如图所示，将小球由静止释放，欲使小球到达最低点后能够以C为圆心做完整圆周运动，试确定H应满足的条件.（运动过程中绳始终不断裂）27. 如下图所示，半径为r，质量不计的圆盘盘面与地面互相垂直.圆心处有一个垂直于盘面的光滑水平固定轴O，在盘的最边缘固定一个质量为m的小球A，在O点的正下方离O点r/2处固定一个质量也为m的小球，现放开盘让其自由转动，问：(1)当A球转到最低点时，两小球的重力势能之和减少

20、了多少？(2)A球转到最低点时的线速度是多少？(3)在转动过程中半径OA向左偏离竖直方向的最大角度是多少？28. 如图所示，质量为m=2kg的小球系在轻质弹簧的一端，另一端固定在悬点O处，将弹簧拉至水平位置A处，且弹簧处于自然状态，弹簧的原长0A=0.3m；然后小球由静止释放，小球到达距O点下方h=0.5m处的B点时速度为VB=2m/s, 求（1）小球从A运动到B的过程中弹簧的弹力做的功和此时弹簧的弹性势能.（2）求该弹簧的劲度系数 29. 如图所示，质量为m的小球，用一轻绳系着在竖直平面内做变速圆周运动，小球过最低点时绳的拉力与小球过最高点时绳的拉力之差为多少？30. V0O1RO一质量为m

21、的质点，系于长为R的轻绳的一端，绳的另一端固定在空间的O点，假定绳是不可伸长的、柔软且无弹性的。今把质点从O点的正上方离O点的距离为的O1点以水平的速度抛出，如图所示。试求；（1）轻绳即将伸直时，绳与竖直方向的夹角为多少？（2）当质点到达O点的正下方时，绳对质点的拉力为多大？31. （15分）某兴趣小组设计了如图所示的玩具轨道，其中“2008”四个等高数字用内壁光滑的薄壁细圆管弯成，固定在竖直平面内（所有数字均由圆或半圆组成，圆半径比细管的内径大得多），底端与水平地面相切.弹射装置将一个小物体（可视为质点）以va5 m/s的水平初速度由a点弹出，从b点进入轨道，依次经过“8002”后从p点水平

22、抛出.小物体与地面ab段间的动摩擦因数0.3，不计其它机械能损失.已知ab段长L1. 5 m，数字“0”的半径R0.2 m，小物体质量m0.01 kg，g10 m/s2.求：小物体从p点抛出后的水平射程.bapva小物体经过数字“0”的最高点时管道对小物体作用力的大小和方向.32. 如图所示，AB是一段位于竖直平面内的光滑轨道，高度为h，末端B处的切线方向水平.一个质量为m的小物体P从轨道顶端A处由静止释放，滑到B端后飞出，落到地面上的C点，轨迹如图中虚线BC所示.已知它落地时相对于B点的水平位移OCl.现在轨道下方紧贴B点安装一水平传送带，传送带的右端与B的距离为l2.当传送带静止时，让P再

23、次从A点由静止释放，它离开轨道并在传送带上滑行后从右端水平飞出，仍然落在地面的C点.当驱动轮转动从而带动传送带以速度v匀速向右运动时（其他条件不变），P的落地点为D.（不计空气阻力）（1）求P滑至B点时的速度大小； （2）求P与传送带之间的动摩擦因数m ；（3）求出O、D间的距离s随速度v变化的函数关系式.33. 如图所示，一轻绳绕过无摩擦的两个轻质小定滑轮O1.O2和质量mB=m的小球连接，另一端与套在光滑直杆上质量mA=m的小物块连接，已知直杆两端固定，与两定滑轮在同一竖直平面内，与水平面的夹角=60°，直杆上C点与两定滑轮均在同一高度，C点到定滑轮O1的距离为L，重力加速度为g

24、，设直杆足够长，小球运动过程中不会与其他物体相碰.现将小物块从C点由静止释放，试求：（1）小球下降到最低点时，小物块的机械能（取C点所在的水平面为参考平面）；CmBO1mAO2（2）小物块能下滑的最大距离；（3）小物块在下滑距离为L时的速度大小.34. 如图所示，半径为R的 圆弧支架竖直放置，支架底ab离地的距离为4R，圆弧边缘C处有一小定滑轮，一轻绳两端分别系着质量分别为m1与m2的物体，挂在定滑轮两边，切m1>m2，开始时m1.m2均静止，切m1.m2视为质点（不计一切摩擦），求：（1）m1经过圆弧最低点a时的速度；（2）若m1到最低点时绳断开，m1与m2之间必须满足什么关系？35.

25、 一质量m2kg的小球从光滑斜面上高h3.5m处由静止滑下，斜面底端紧接着一个半径R1m的光滑圆环，如图所示，试求：(1)小球滑至圆环顶点时对环的压力(2)小球至少应从多高处由静止滑下才能越过圆环最高点(3) 小球从2m处由静止滑下时将在何处脱离圆环.（g10m/）36. 如图所示，质量可忽略不计，半径为R的薄圆盘，可绕过圆心O的光滑水平轴，在竖直平面内自由转动.在圆盘边缘的A点和距圆心R/2的B点分别固定质量分别为、的小物块（可视为质点），已知2，且OA与OB垂直，现让圆盘从OA连线为水平位置时开始由静止释放.当OA转到竖直位置时，求此时：（1）圆盘转动的角速度；（2）物块对圆盘作用力的大小

26、和方向.37. 一圆环A套在一均匀圆木棒B上，A的高度相对B的长度来说可以忽略不计A和B的质量都等于m，A和B之间的滑动摩擦力为f（f < mg）开始时B竖直放置，下端离地面高度为h，A在B的顶端，如图所示让它们由静止开始自由下落，当木棒与地面相碰后，木棒以竖直向上的速度反向运动，并且碰撞前后的速度大小相等设碰撞时间很短，不考虑空气阻力，问：在B再次着地前，要使A不脱离B， B至少应该多长？hAB38. 图311一个质量为0.20kg的小球系于轻质弹簧的一端。套在光滑竖立的圆环上，弹簧的上端固定于环的最高点，环的半径R=0.5m,弹簧的原长l0=0.5m,劲度系数为4.8N/m,如图31

27、1所示。若小球从B点有静止开始滑到最低点C时，弹簧的弹性势能E=0.60J。求；（1）小球到C点时速度vc的大小.（2）小球在C对环的作用力(g=10m/s2).39. 如图所示轻杆长1m，其两端各连接质量为1kg的小球，杆可绕距B端0.2m处的轴O在竖直平面内转动，轻杆由水平从静止转至竖直方向，A球在最低点的速度为4m/s。求： A B O （1）A球此时对杆的作用力大小及方向（2）B球此时对杆的作用力大小及方向40. 如图所示，A物体用板托着，位于离地h=1.0m处，轻质细绳通过光滑定滑轮与A、B相连，绳子处于绷直状态，已知A物体质量M=1.5，B物体质量m=1.0kg，现将板抽走，A将拉

28、动B上升，设A与地面碰后不反弹，B上升过程中不会碰到定滑轮，问：B物体在上升过程中离地的最大高度为多大？取ABh41. 如图所示，一质量不计的直角形支架两端分别连接质量为m和2m 的小球A和B，支架的两直角边长度分别为2l和l，支架可绕固定轴O在竖直平面内无摩擦转动，开始时OA边处于水平位置，由静止释放，试求两小球总的最小重力势能和最大动能。42. 城市中为了解决交通问题，修建了许多立交桥，如图所示，桥面为圆弧形的立交桥AB，横跨在水平路面上，长为L=200m，桥高h=20m。可以认为桥的两端A、B与水平路面的连接处的平滑的。一辆汽车的质量m=1040kg，以=25m/s的速度冲上圆弧形的立交

29、桥，假设汽车冲上立交桥后就关闭了发动机，不计车受到的阻力。试计算：（g取10m/s2）小汽车冲上桥顶时的速度是多大？小汽车在桥顶处对桥面的压力的大小。ABLh43. 如图所示，一固定在竖直平面内的光滑的半圆形轨道ABC，其半径R5.0m，轨道在C处与水平地面相切。在C处放一小物块，给它一水平向左的初速度v05m/s，结果它沿CBA运动，通过A点，最后落在水平面上的D点，求C、D间的距离s。取重力加速度g10m/s2。44. 如图所示，支架的质量为M，转轴O处用长为L的轻绳悬挂一质量为m的小球。若小球在竖直面内做圆周运动，到达最高点时恰好支架对地面无压力。设M=3m。0mM0求：（1）小球在最高

30、点时的速度大小是多少？（2）支架对地面的最大压力是多少？ 45. 如图所示，半径R=0.50m的光滑圆环固定在竖直平面内。轻质弹簧的一端固定在环的最高点A处，另一端系一个质量m=0.20kg的小球。小球套在圆环上。已知弹簧的原长为，劲度系数K=4.8N/m。将小球从如图所示的位置由静止开始释放。小球将沿圆环滑动并通过最低点C，在C点时弹簧的弹性势能。求：小球经过C点时的速度的大小。小球经过C点时对环的作用力的大小和方向。46. 质量为0.02 kg的小球，用细线拴着吊在沿直线行驶着的汽车顶棚上，在汽车 距车站15 m处开始刹车，在刹车过程中，拴球的细线与竖直方向夹角37°保持不变，如

31、图所示，汽车到车站恰好停住.求：(1)开始刹车时汽车的速度；(2)汽车在到站停住以后，拴小球细线的最大拉力. (取g10 ms2，sin37°0.6，cos37°0.8) 47. OABC固定的光滑圆弧轨道ABC处在竖直平面内，圆轨道半径为R，半径OA处于水平，OB处于竖直方向，BOC=60º，如图所示。一个小物体质量为m，从A处由静止开始滑下，沿圆弧轨道运动，从C点飞出。求：小物块通过B点时的速度大小。小物块经过B点时对轨道的压力的大小和方向。小物块从C点飞出时的速度大小和方向。2012年高考模拟题参考答案（仅供参考）四.计算题答案:1. 解:(1)在C点对轨道

32、的压力等于重力的倍,由牛顿第三定律得,在C点轨道对小球的支持力大小为mg设小球过C点速度v1-2分P到C过程,由机械能守恒:-1分解得:-1分(2)设小球能到达O点,由P到O,机械能守恒,到O点的速度v2:-2分设小球能到达轨道的O点时的速度大小为v0,则mg=v0-1分v2>v0所以小球能够到达O点.-1分(3)小球在O点的速度离开O点小球做平抛运动:水平方向:-1分竖直方向:-1分且有:-1分解得:-1分2. 解:(1)由机械能守恒定律,得:(2)人飞出作平抛运动,最高点速度v最小时人刚好落在平台上,则S=t解得:(3)设蹬地瞬间人做功W,由动能定理,有:3. （1）滑块在圆盘上做圆

33、周运动时，静摩擦力充当向心力，根据牛顿第二定律，可得：mg=m2R 代入数据解得：=5rad/s （2）滑块在A点时的速度：VA=R=1m/s 在B点时的机械能EB=mvA2/2 =0.5J （3）滑块在从A到B的运动过程中机械能守恒mgh+ mvA2/2= mvB2/2 vB=5m/s 滑块沿BC段向上运动时的加速度大小：a1=g（sin37°+cos37°）=10m/s2 返回时的加速度大小：a2=g（sin37°-cos37°）=2m/s2 BC间的距离：sBC=vB2/2a1-1/2 a2（t-vB/a1）2=1.24m 4. 解:为使小球能绕B

34、点做完整的圆周运动,则小球在D对绳的拉力F1应该大于或等于零,即有:根据机械能守恒定律可得由以上两式可求得:5. 解:在A下降B上升的过程中,A、B系统机械能守恒,由机械能守恒定律得:解得代入数据有2m/sA着地后,B做竖直上抛运动,竖直上抛能上升的高度为代入数据有0.2mB物体上升过程中距地面的最大高度为1.2m6. 解:B点速度在竖直方向的分量:m/s竖直方向的分运动为自由落体运动:m根据机械能守恒定律,有:解得m2/s2根据牛顿第二定律,有解得F'C=42N根据牛顿第三定律,F=F'=42N,方向竖直向下.设小球能到达D点,根据机械能守恒定律,有:解得,即小球能到达D点.

35、根据牛顿定律,有代入数据,解得小球受到的压力根据牛顿第三定律,小球对轨道的压力为FD=F'D=12N,方向竖直向下.7. 解析:设小球在最低点的速度大小为v0,在最高点的速度大小为v.小球在线拉力T和重力mg作用下,绕O点在竖直面内做变速率圆周运动.由于拉力不做功,小球向下运动过程中动能转化为势能,小球与地球系统机械能守恒,以小球在最低点时的重力势能为零,有mv02+0=mv2+mg（2l）小球在最高点时受重力mg与拉力T的作用,两力方向都竖直向下.根据牛顿第二定律有T+mg=m重力mg恒定,v越大,T也越大,v越小T也越小.v最小的条件为T=0由两式得v=代入得v0=8. 解:小球的

36、运动可分为三个过程:第一过程:小球做平抛运动.设绳即将伸直时,绳与竖直方向的夹角为,如图所示,则OV0VVV/,其中联立解得.第二过程:绳绷直过程.绳棚直时,绳刚好水平,如图所示.由于绳不可伸长,故绳绷直时,V0损失,小球仅有速度V,且.第三过程:小球在竖直平面内做圆周运动.设小球到达O点正下方时,速度为V,根据机械能守恒守律有:设此时绳对小球的拉力为T,则,联立解得:.9. 解:(1)在B点:(2分)得:(1分)(2)对B到C过程:有:(1分)得:(1分)到达C点前:(1分)得:(1分),方向竖直向下(1分).到达C点后:(1分)得:(1分),方向竖直向上(1分).(3)设能到达E点,且速度

37、大小为vE对A到B过程有:(1分)得:(1分)对C到E过程:有:(1分)得:,能过E点.(1分)由:和得:(1分)10. 解:(1)由几何关系可知,AB间的距离为R(1分)小物块从A到B做自由落体运动,根据运动学公式有(2分)代入数据解得vB=4m/s,方向竖直向下(2分)(2)设小物块沿轨道切线方向的分速度为vBx,因OB连线与竖直方向的夹角为60°,故vBx=vBsin60°(2分)从B到C,只有重力做功,根据机械能守恒定律有(2分)代入数据解得m/s(1分)在C点,根据牛顿第二定律有(2分)代入数据解得N(1分)再根据牛顿第三定律可知小物块到达C点时对轨道的压力FC=

38、35N(1分)(3)小物块滑到长木板上后,它们组成的系统在相互作用过程中总动量守恒,减少的机械能转化为内能.当物块相对木板静止于木板最右端时,对应着物块不滑出的木板最小长度.根据动量守恒定律和能量守恒定律有mvC=(m+M)v(2分)(2分)联立、式得代入数据解得L=2.5m(2分)11. 解:(1)A、B、C三物体系统机械能守恒.B、C下降L,A上升L时,A的速度达到最大.2mgLMgL=(M+2m)V22分V=(2)当C着地后,A、B二物体系统机械能守恒.B恰能着地,即B物体下降L时速度为零.MgLmgL=(M+m)V2将V代入,整理后得:M=m若Mm,B物体将不会着地.Mghmgh=(M

39、+m)V2h=HL=L+h=L+若M=m,B恰能着地,A物体再上升的高度等于L.H2=2L若Mm,B物体着地后,A还会上升一段.MgLmgL=(M+m)(V2v2)V2=h=H3=2L+h=2L+12. 解:(1)设钢珠在轨道最高点的速度为,在最高点,由题意从发射前到最高点,由机械能守恒定律得:(2)钢珠从最高点飞出后,做平抛运动由几何关系从飞出到打在得圆弧面上,由机械能守恒定律:联立、解出所求13. （1）29.8N（30N）；方向竖直向下（2）4.8N（5N）；方向竖直向下14. 解:在b球落地前,a.b球组成的系统机械能守恒,且a.b两球速度大小相等,设为v,根据机械能守恒定律有:3mg

40、h2mgh(2m3m)v2,解得:b球落地时,a球高度为h,之后a球向上做竖直上抛运动,由机械能守恒有,(2m)v22mghh0.2h所以a球可能达到的最大高度为H=h+0.2h=1.2h.15. 解:(1)该同学通过C点时有代入数据得(2)人和滑板从A点运动到C的过程中,根据动能定理有代入数据解得16. 解:（1）小球开始做平抛运动,有:2分根据几何关系,有:2分代入数据,解得:2分（3）小球从点B运动到点C时,满足机械能守恒定律,有:2分又:1分代入数据,解得:2分所以小球能从C点飞出.17. 解:(1)对小物块由A到B有（2分）在B点（2分）(2)对小物块由B到O有（2分）其中且在O点有

41、得（3分）N=43N；由牛顿第三定律物体对轨道压力N=43N.（1分）（3）物块沿斜面上滑:（2分）物块沿斜面下滑:（2分）由机械能守恒有（1分）小物块上升到最高点的时间:（1分）小物由最高点回到D点时间:（1分）有得18. 解:(1)小球恰好能做完整的圆周运动,则小球通过A点时细线的拉力为零,根据向心力公式有:解得:(2)小球从A点运动到B点,由机械能守恒定律有:解得:小球在B点时根据牛顿第二定律有:解得:T6mg(3)小球运动到B点时细线断裂,小球做平抛运动,有:xvBt解得:.19. 解:设物块在圆形轨道最高点的速度为v,由机械能守恒定律得mgh=2mgRmv2物块在最高点mgN=mVh

42、2.5R按题的需求,N=5mg,Vh5Rh的取值范围是2.5Rh5R20. 解:(1)小球离开平台后做平抛运动,小球正好落到水平地面木板的末端,则H=联立式得:设释小球的高度为h1,则:(2)由机械能守恒定律可得:小球由离开平台后做平抛运动,可看做水平方向的匀速直线运动和竖直方向的自由落体运动,则:得:Ek=3.25h21. 解:(1)滑块在圆盘上做圆周运动时,静摩擦力充当向心力,根据牛顿第二定律可得,代入数据得:(2)滑块在A点时的速度:从A到B的运动过程中由动能定理得:在B点时的机械能:(3)滑块在B点的速度:滑块沿BC段向上运动时的加速度大小:返回时的加速度大小:BC间的距离:22. 解

43、:(1)设小球离开轨道进入小孔的时间为t,则由平抛运动规律得:小球在轨道上运动过程中机械能守恒,故有联立解得:(2)在小球做平抛运动的时间内,圆筒必须恰好转整数转,小球才能钻进小孔,即所以)23. （1）粘合后的两球飞出轨后做平抛运动，竖直方向分运动为自由落体运动，有 解得 （2）设球A的质量为m，碰撞前速度大小为v1把球A冲进轨道最低点时的重力势能为0，由机械能守恒定律知 设碰撞后粘合在一起的两球速度大小为v2，由动量守恒定律知 飞出轨道后做平抛运动，水平方向分运动为匀速直线运动，有 综合式得 24. （1）受力图见右根据平衡条件，应满足 拉力大小F=mgtanTFmg（2）运动中只有重力做

44、功，系统机械能守恒则通过最低点时，小球的速度大小根据牛顿第二定律 解得轻绳对小球的拉力，方向竖直向上25. 2.53s【解析】本题考查平抛、圆周运动和功能关系。设赛车越过壕沟需要的最小速度为v1，由平抛运动的规律 解得 设赛车恰好越过圆轨道，对应圆轨道最高点的速度为v2，最低点的速度为v3，由牛顿第二定律及机械能守恒定律 解得 m/s通过分析比较，赛车要完成比赛，在进入圆轨道前的速度最小应该是 m/s设电动机工作时间至少为t，根据功能原理 由此可得 t=2.53s26. 欲使小球到达最低点后能够以C为圆心做完整圆周运动，则小球到达圆周最高点的速度至少应为则由：机械能守恒定律可得：解得： 则：

45、27. 以C点为零势能点，以对AB组成的系统，(1）当A球转到最低点过程中两小球的重力势能之和减少了：EP减1=mgr-mgr/2=mgr/2(2) 依机械能守恒定律：EP减1=EK增 又VA=r VB=r/2 VA=2VB 由可解得： (3)设OA向左偏离竖直方向的最大角度为，系统的初始机械能系统末的始机械能：由机械能守恒定律：E1=E2 可解得：28. （1）小球从A至B过程中，取小球下落的最低点B为零势能点，依机械能守恒定律： 可得：EP弹=2 J ，所以弹簧在此过程做的负功，大小为2J（2）在B点：X=（0.5-0.3）m=0.2 m, 可得K=180N/m29. 设小球过最低点时速度

46、为v1，绳的拉力为T1，过最高点时速度为v2，绳的拉力为T2，绳长为L在最低点：T1mgmv12/L在最低点：T2mgmv22/L由机械能守恒得：mv12/2mv22/2mg（2L） T1T26mg30. 错解：很多同学在求解这道题时，对全过程进行整体思维，设质点到达O点的正下方时速度为V,根据能量守恒定律可得： 根据向心力公式得：，解得：.分析纠错：上述解法是错误的。这些同学对物理过程没有弄清楚，忽视了在绳被拉直瞬时过程中机械能的瞬时损失。其实质点的运动可分为三个过程：第一过程：质点做平抛运动。设绳即将伸直时，绳与竖直方向的夹角为，如图所示，则，其中联立解得。第二过程：绳绷直过程。绳棚直时，

47、绳刚好水平，如图31. 解：设小物体运动到p点时的速度大小为v，对小物体由a到p过程应用动能定理得： svt解得：s0.8 m设在数字“0”的最高点时管道对小物体的作用力大小为F，有：解得：F0.3 N方向竖直向下32. （1）物体P在AB轨道上滑动时，物体的机械能守恒，根据机械能守恒定律得物体P滑到B点时的速度为（3分）（2）当没有传送带时，物体离开B点后作平抛运动，运动时间为t，当B点下方的传送带静止时，物体从传送带右端水平抛出，在空中运动的时间也为t，水平位移为，因此物体从传送带右端抛出的速度（2分）.根据动能定理，物体在传送带上滑动时，有（1分）.解出物体与传送带之间的动摩擦因数为（1

48、分）.（3）当传送带向右运动时，若传送带的速度，即时，物体在传送带上一直做匀减速运动，离开传送带的速度仍为，落地的水平位移为，即sl（2分）.当传送带的速度时，物体将会在传送带上做一段匀变速运动.如果尚未到达传送带右端，速度即与传送带速度相同，此后物体将做匀速运动，而后以速度v离开传送带.v的最大值为物体在传送带上一直加速而达到的速度，即.由此解得（1分）.当，物体将以速度离开传送带，因此得O、D之间的距离为（1分）.当，即时，物体从传送带右端飞出时的速度为v，O、D之间的距离为（1分）.综合以上的结果，得出O、D间的距离s随速度v变化的函数关系式为： （1分）33. （1）设此时小物块的机械

49、能为E1.由机械能守恒定律得 （3分）（2）设小物块能下滑的最大距离为sm，由机械能守恒定律有 （2分）而 （1分）代入解得 ； （2分）（3）设小物块下滑距离为L时的速度大小为v，此时小球的速度大小为vB，则 （1分） （2分） 解得 （2分）感悟与反思：本题要求正确判断CO1长度是现变短后变长，从而知道小球是先上升后下降，CO垂于杆时小球速度为零；物块速度为零时小球速度也为零。最后一问要求学生正确处理A.B两物体之间的速度关系，即两者沿绳速度相等。综合考查了运动分析.能量守恒定律.运动的合成与分解等知识。学生对第一问难以上手，所以本题三问的区分度并不好。34. 解：（1）设m1运动到最低点时速度为v1，m2的速度为v2，将