2019高考数学理科全国卷III真题试卷及答案解析

1、绝密启用前2019 年普通高等学校招生全国统一考试理科数学（全国卷III ）注意事项：1答卷前，考生务必将自己的姓名和准考证号填写在答题卡上。2回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上。写在本试卷上无效。3考试结束后，将本试卷和答题卡一并交回。一、选择题：本题共12 小题，每小题5 分，共 60 分。在每小题给的四个选项中，只有一项是符合题目要求的。21已知集合A 1,0,1,2， B xx2 1，则 AI BA1,0,1B0,1C1,1D0,1,22若z（1 i） 2i ，则 z=A

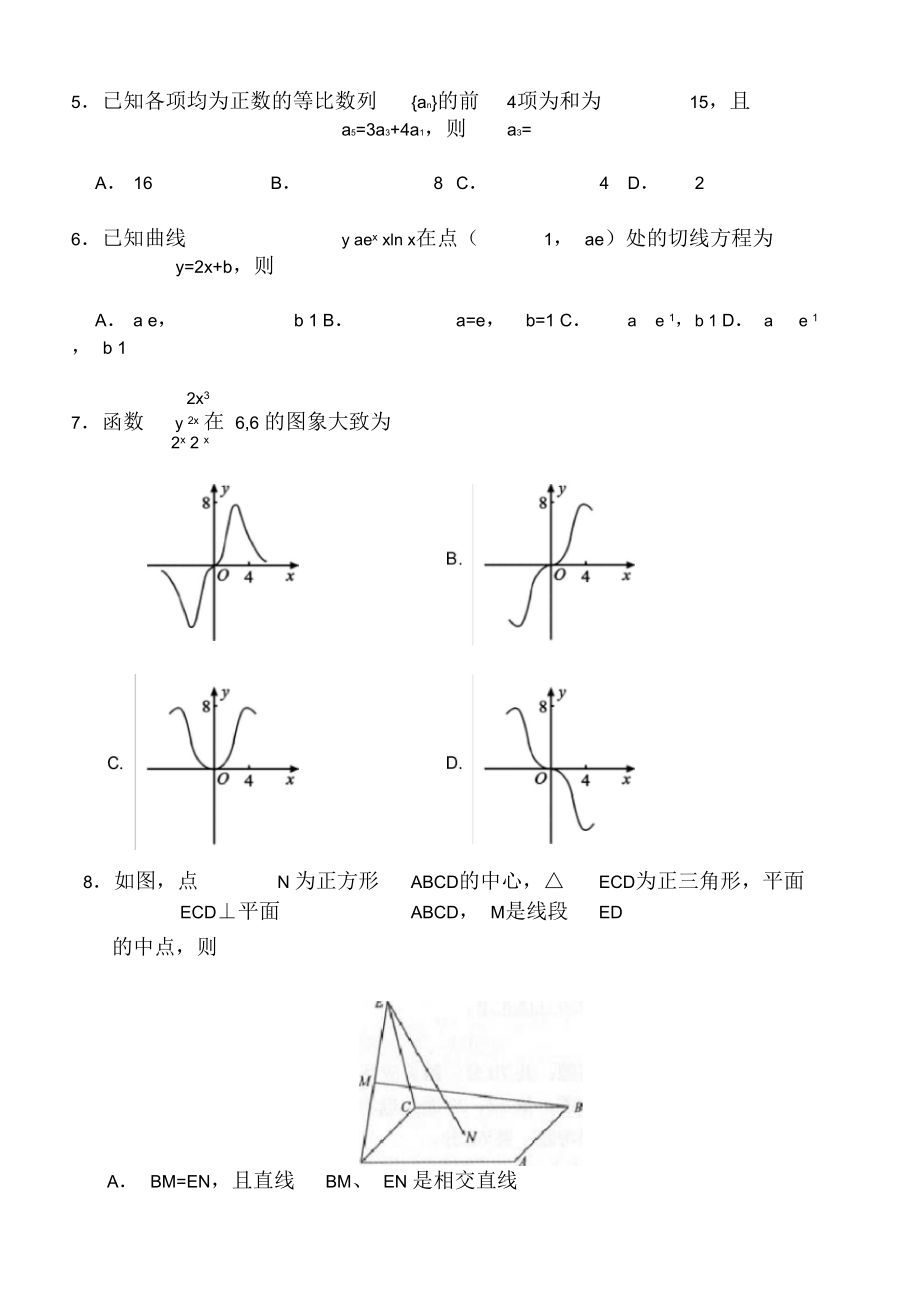
2、1 iB1+iC 1 iD1+i3西游记三国演义水浒传和红楼梦是中国古典文学瑰宝，并称为中国古典小说四大名著. 某中学为了解本校学生阅读四大名著的情况，随机调查了100 学生， 其中阅读过西游记或红楼梦的学生共有90 位，阅读过红楼梦的学生共有80 位，阅读过西游记且阅读过红楼梦的学生共有60 位，则该校阅读过西游记的学生人数与该校学生总数比值的估计值为A 0.5B 0.6C 0.7D 0.84（1+2x2 ）（1+x） 4的展开式中x3的系数为A 12B 16C 20D 245已知各项均为正数的等比数列an的前4项为和为15，且a5=3a3+4a1，则a3=A16B8C4D26已知曲线y a

3、ex xln x在点（1， ae）处的切线方程为y=2x+b，则Aa e，b 1 Ba=e，b=1 Cae 1，b 1 Dae 1 ， b 12x37函数y 2x 在 6,6 的图象大致为2x 2 x8如图，点N 为正方形ABCD的中心，ECD为正三角形，平面ECD平面ABCD， M是线段ED的中点，则A BM=EN，且直线BM、 EN 是相交直线B BM EN，且直线BM， EN 是相交直线C BM=EN，且直线BM、 EN 是异面直线D BM EN，且直线BM， EN 是异面直线9执行下边的程序框图，如果输入的为 0.01 ，则输出s的值等于A. 2142B. 2 215C. 2 216D

4、. 2127210 双曲线C： x42y =1 的右焦点为F， 点 P在 C的一条渐进线上，O为坐标原点，若 PO = PF则PFO的面积为A324B32C 2 2D 3 211设 f x 是定义域为R的偶函数，且在0,单调递减，则A f （ log 3 1 ） f4322 2 ） f （ 2 3 ）23Bf （ log 31 ） f （ 2 3） f （ 2 2 ）42232C f （ 2 2 ） f （ 2 3 ） f （ log 3 1 ）224D f22 3 ） f32 2 ） flog 3 1 ）412设函数f x =sin （ x ） （ > 0），已知 f x 在 0,2

5、有且仅有5 个零点，下述四个5结论： fx在（0,2）有且仅有3个极大值点 fx在（0,2）有且仅有2个极小值点 fx在（0,）单调递增1012 29 的取值范围是 12 ， 15 设 F1， F2为椭圆C: x + y 1 的两个焦点，M为 C上一点且在第一象限. 若 MF1F2为等腰 36 20 三角形，则M的坐标为 . 16 学生到工厂劳动实践，利用 3D打印技术制作模型. 如图， 该模型为长方体ABCD A1B1C1D1 挖去四棱锥O EFGH后所得几何体，其中O为长方体的中心，E， F， G， H 分别为所在棱 的中点，AB= BC= 6cm, AA1 = 4cm ， 3D打印所用原

6、料密度为0.9 g/cm3，不考虑打印损 耗，制作该模型所需原料的质量为. ）5 10其中所有正确结论的编号是A B C D 4 小题，每小题5 分，共 20 分。13已知a， b 为单位向量，且a· b=0，若c 2a 5b，则 cos a,c .S1014记Sn为等差数列an的前n 项和，a1 0， a2 3a1，则.S570 分。解答应写出文字说明、证明过程或演算步骤。第1721 题为必考题，每个试题考生都必须作答。第22、 23 题为选考题，考生根据要求作答。60分。17（12 分）为了解甲、乙两种离子在小鼠体内的残留程度，进行如下试验：将 200 只小鼠随机分成A、B两组，

7、每组100 只，其中A组小鼠给服甲离子溶液，B组小鼠给服乙离子溶液，每组小鼠给服的溶液体积相同、摩尔浓度相同经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比. 根据试验数据分别得到如下直方图：记 C为事件：“乙离子残留在体内的百分比不低于 5.5”，根据直方图得到P（C）的估计值为 0.70 （ 1）求乙离子残留百分比直方图中a，b 的值；（ 2）分别估计甲、乙离子残留百分比的平均值（同一组中的数据用该组区间的中点值为代表）18（12 分）ACABC的内角A、B、C的对边分别为a、b、c，已知asinbsinA2（ 1）求B；（ 2）若ABC为锐角三角形，且c=1，求ABC面积的取

8、值范围19（12 分）图 1 是由矩形ADEB、 Rt ABC和菱形BFGC组成的一个平面图形，其中AB=1， BE=BF=，2FBC=60°，将其沿AB， BC折起使得BE与 BF重合，连结DG，如图2.（ 1）证明：图2 中的A， C， G， D 四点共面，且平面ABC平面BCG；E（ 2）求图2 中的二面角B-CG-A的大小.20（12 分）已知函数f （x） 2x3 ax2 b .（ 1）讨论 f （x） 的单调性；（ 2）是否存在a,b， 使得 f（x） 在区间 0,1的最小值为1且最大值为1？若存在，求出 a,b的所有值；若不存在，说明理由.x2121已知曲线C： y=

9、x ， D为直线 y= 1 上的动点，过D作C的两条切线，切点分别为A， B.221）证明：直线AB 过定点：52)若以E(0， 25 )为圆心的圆与直线AB相切，且切点为线段AB的中点，求四边形ADBE.(二)选考题：共10 分。请考生在第22、 23 题中任选一题作答。如果多做，则按所做的第一题计分。22 选修 4-4：坐标系与参数方程( 10分)如图，在极坐标系Ox中，A(2,0) ， B( 2, 4)， C( 2, 4 )， D(2, )，弧 ?AB ， ?BC ， C?D 所在圆的圆心分别是(1,0)， (1, )， (1, ) ，曲线 M1 是弧?AB，曲线M2是弧?BC ，曲线M

10、3是弧 C?D .( 1)分别写出M 1 ， M 2 ， M 3 的极坐标方程；( 2)曲线M 由 M1 ， M2， M3构成，若点P 在 M上，且 |OP |3，求 P的极坐标.23 选修 4-5：不等式选讲( 10分)设 x, y, z R ，且 x y z 1 .(1)求(x1)2(y1)2(z1)2的最小值；1(2)若(x2)(y1)(za)成立，证明：a 3或 a 1 .32019 年普通高等学校招生全国统一考试理科数学(全国卷III )答案及解析1. A解答： B x|x2 1 x| 1 x 1 ，所以 A B 1,0,1 .2. D解答： z(1 i) 2i , z 2i 2i(

11、1 i) i(1 i) 1 i .1 i (1 i)(1 i )3. C解答： 90 80 60 0.7 1004. A3332133解答：由题意可知含x 的项为 1 C4 1 x 2x C4 1 x 12x ，所以系数为125. C解答：设该等比数列的首项a1 ，公比q ，由已知得，a1q43a1q2 4a1 ，因为 a1 0且 q 0，则可解得q 2，又因为a1(1 q q2 q3) 15 ，即可解得a1 1 ，则a3 a1q2 4 .6. D解析：令f (x) aex xln x，则 f (x)1ae ln x 1 ， f (1) ae 1 2 ，得 aef (1) 7. B 解析：ae

12、 2 b ，可得b1. 故选 D.2x32(f(x) 2x 2x， f( x) 2x3 x)2x2x32x 2 xf (x) ， f (x) 为奇函数，排除选项C. 又f (4)2 432 432 42 48 ，根据图像进行判断，可知选项B 符合题意.24 2 4248. B解析：因为直线， 都是平面内的直线，且不平行，即直线， 是相交直线，设正方形的边长为 ，则由题意可得：，根据余弦定理可得：，所以9. C解析：，故选 B.第一次循环：第二次循环：第三次循环：第四次循环：第七次循环：此时循环结束，可得. 故选 C.10. A 解析：0可得一条渐近线方程为2yx2PFO 中 |PO | |PF

13、 |过点P做 PH直 OF 因为 tanPOF= 2 PO 3 S2 得到2 ; 所以PFO32; 故选 A;11. C解析 :(0,依据题意函数为偶函数且函数在1f(log3 ) f( log34) f(log34)4；)单 调 递 减 ，则函数在30 22 2又因为,0) 上 单 调 递 增 ； 因1 log34；321f(2 2)f(2 3) f(log3 )4 ；故选 C.12.D根据题意，画出草图，由图可知2x1, x2 ，所以 245x1x229512x1x229102452954 对；125 . 填空题x1, x2 ，29，10310 f (x) 在 11250 ，图像中y 轴右

14、侧第一个最值点为最大值点，故0,21013.有 2 个或3 个极小值点，故2 错；495100，故3 对 .2解析：r2 cr2a22ar5br9 ，r4a3，cos a, c23rr14.解析：设该等差数列的公差为d ， a2 3a1 ，a1d 3a1 ，故d 2a1a10,d 0 ，10 a1 a10S10S55 a1 a52 2a1 9d2a1 4d2 10d5d4.215.(3, 15)解析：2 x C：362 y201 可知， a 6 ，c 4 ，由M 为 C 上一点且在第一象限，故等腰三角形MF1F2MF1F1F28， MF2 2aMF14 , sinF1F2M82 228154y

15、MMF2sinF1F2M15 ，代入2C： 362 y201 可得xM3. 故 M 的坐标为(3, 15) .16.118.8解答：S四边形EFGH 4m V 0.9三解答题17.解析解答:1321232118.8g.12cm2， V 66412 3 132 cm3.1）依题意得a 0.2 0.150.70.350.05 b 0.150.15 0.2 a 1b0.10.2 50.3 64.05, ，乙离子残留百分比的平均值为（ 2）0.15 2 0.2 3 0.3 40.05 3 0.1 4 0.15 5得到甲离子残留百分比的平均值为18.0.1 6 0.05 7 4.050.2 7 0.15

16、 8 5.75.7.20.（1）3（ 2）见解析解析：(1) 因B cos2sin Asin sin Bsin A 为2sin Asin 结合正弦定理sin Bsin A,得BB B1Bsin B 2sin cos sin, B22 , 即 22 ；得到263 ；0A(2) 因asin AACbsin BsinC1 acsin2B1C 2,02 sin Ccsin A2所C 2, 又133sin A若 A越大 sin A越大， 则 C越小 sinC 越小；sin C ; 又因为 sin AssiinnCA (21,2)sin Asin C 越大 ） ； 所以 sin C(12,2)23 , A

17、,C 为锐角，19.解析：证明： （ 1）由题意知，又，平面，又平面，平面平面.（2） 分别取， 的中点为， ，连结， ，则，四边形为棱形，且60 ，又平面，即平面，以点 为坐标原点，分别为 轴， 轴， 轴，建立空间直角坐标系，设平面的一个法向量为,，令，则得到，平面的一个法向量为，, 故二面角的大小为.答案：见解析解析：21) f '(x) 6x2 2ax 6x(x a)3当 a 0时， f '(x) 6x2 0，此时 f(x) 在 (,)单调递增 .a0 ，解得 0 x .3a当 a 0时，令 f '(x) 0 ，解得 x a 或 x 0，令 f '(x)3

18、此时 f (x) 在 (,0),( a ,) 单调递增，在(0, a)单调递减.33a0 ，解得x 0 .3a当 a 0时，令 f '(x) 0 ，解得 x 0或 x a ，令 f '(x)3此时 f (x) 在 (, a),(0,) 单调递增，在(a ,0) 单调递减.33综上可得，当a 0时， f (x) 在 (,)单调递增.aa0时，f(x) 在 (,0),( a ,3a0 时，f (x) 在 (, a),(0,32)由(1)中结论可知，当a) 单调递增，在(0, a) 单调递减.a) 单调递增，在( ,0) 单调递减.30时， f (x) 在 0,1 单调递增，此时 f

19、 (x)min f(0) b 1,f (x)max f (1) 2 a b 1， a 0,b1 ，满足题意a当 a 0时，若1 ，即 a 3，则 f (x) 在 0,1 单调递减，3此时 f (x)min f(1) 2 a b 1, f(x)maxf(0) b 1， a 4,b 1，满足题意若 a 1 ，即 0 a 3，则 f(x) 在 0, a 单调递减，在a ,1单调递增.333323aaaa此时 f (x)min f ( ) 2 a bb 1327927f (0) b, f (1) b 2 a当 0 a 2 时，f (x)maxf (1) b 2 a 1 ，由 可得 a 3 3, b 3

20、 3 1 ，与 0 a 2矛盾，故不成立.当 2 a 3时， f(x)max f(0) b 1 ，由 可得 a 33 2, b 1 ，与 2 a 3矛盾，故不成立.综上可知，a 0,b1 或 a 4,b 1 满足题意.21. 答案：见解析；解答：11( 1)当点 D 在 (0,) 时，设过D 的直线方程为y k0x，与曲线C 联立化简得2222x2 2k0x 1 0 ，由于直线与曲线相切，则有4k02 4 0，解得k01 ，111并求得 A, B 坐标分别为( 1, ),(1, )，所以 直线 AB 的方程为y ；222当点 D 横坐标不为0 时，设直线AB 的方程为y kx m ( k 0)

21、 ，由已知可得直线y kx mAB 不过坐标原点即m0 ，联立直线AB 方程与曲线C 的方程可得，x2 ，y2消 y 并化简得x2 2kx2m 0，有两个交点24k2 8m 0，设 A(x1, y1 ) ， B(x2 , y2 ) ，根据韦达定理有，x1 x2 2k ， x1x22m ，x2由已知可得曲线C 为抛物线等价于函数f (x) x 的图像，则有 f (x) x ，则抛物线在A(x1 , y1) 上的切线方程为y y1 x1 (x x1) ，同理，抛物线在B(x2, y2)上的切线方程为y y2 x2(x x2) ，联立，并消去x 可得 yy1x1yy2x2x2x1 ，1y 上，则有2

22、221x121 x22化简得，22x122x2x2x1 ，(x1x2 1)( x2 x1)2x1x2x2x1 ，k 0， x1x1x2 12m 11即 1 21 ，即为1 ，解得m ，经检验2x1x24m2x2 ，1m 满足条件，211所以直线AB 的方程为y kx 1 过定点 (0, 1 ) ，221综上所述，直线AB 过定点 (0, 1 ) 得证 .21( 2)由(1)得直线AB 的方程为y kx ，211当 k 0时，即直线AB 方程为 y ，此时点D 的坐标为(0,)，2251以 E(0, ) 为圆心的圆与直线AB 相切于 F (0, ) 恰为 AB 中点，2211此时SADBEAB ED 2 3 3；22k 0 时，直线AB 方程与曲线方程联立化简得x2 2kx 1 0 ，2x1 x2 2k ， x1x21 ， y1 y