北师大版九级数学下册第三章圆第二节圆的对称性

1、2015.013.2 3.2 圆的对称性圆的对称性O O九年级数学九年级数学(下下)第三章第三章 圆圆定义一：定义一： 在同一平面内，线段在同一平面内，线段OA绕它固定的一个端点绕它固定的一个端点O旋转旋转一周，另一个端点一周，另一个端点A随之旋转所形成的图形叫随之旋转所形成的图形叫圆圆。固定的端点固定的端点O叫做叫做圆心圆心，线段，线段OA叫做叫做半径半径。、从运动和集合的观点理解圆的定义：、从运动和集合的观点理解圆的定义：定义二：定义二：圆圆是到定点的距离等于定长的点的集合。是到定点的距离等于定长的点的集合。、证明几个点在同一个圆上的方法。、证明几个点在同一个圆上的方法。 要证明几个点在同

2、一个圆上，只要证明这几个点要证明几个点在同一个圆上，只要证明这几个点与一个定点的距离相等。与一个定点的距离相等。、点与圆的位置关系：、点与圆的位置关系：设设 的半径为的半径为r，则点，则点P与与 O的位置关系有：的位置关系有：（）点在（）点在 上上 r（）点在（）点在 内内 r（）点在（）点在 外外 r知知识识回回顾顾复习提问：复习提问：1 1、什么是轴对称图形？我们在学过、什么是轴对称图形？我们在学过哪些轴对称图形？哪些轴对称图形？如果一个图形沿一条直线对折，直线两旁的如果一个图形沿一条直线对折，直线两旁的部分能够互相重合，那么这个图形叫轴对称部分能够互相重合，那么这个图形叫轴对称图形。如线

3、段、角、等腰三角形、矩形、菱图形。如线段、角、等腰三角形、矩形、菱形、等腰梯形、正方形形、等腰梯形、正方形2 2、我们所学的圆是不是轴对、我们所学的圆是不是轴对称图形呢？称图形呢？.圆的对称性圆的对称性圆是轴对称图形吗？圆是轴对称图形吗？ 如果是如果是,它的对称轴是什么它的对称轴是什么?你能找到多少条你能找到多少条对称轴？对称轴？O你是用什么方法解决上述问题的你是用什么方法解决上述问题的?圆是中心对称图形吗？圆是中心对称图形吗？ 如果是如果是,它的对称中心是什么它的对称中心是什么?你能你能找到多少个对称中心？找到多少个对称中心？你又是用什么方法解决这个问题的你又是用什么方法解决这个问题的? 想

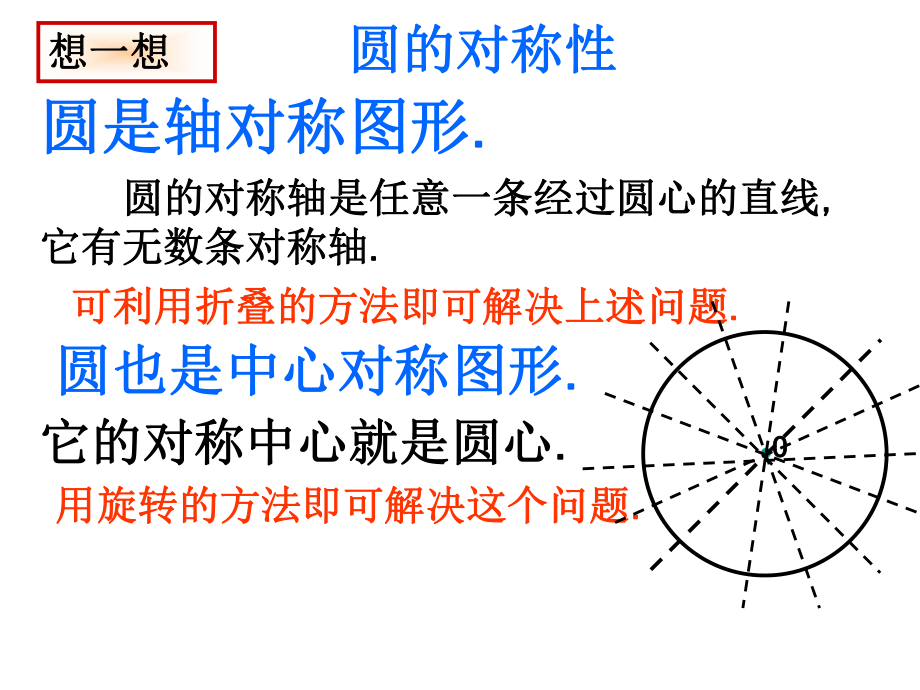
4、一想想一想圆是轴对称图形圆是轴对称图形. .想一想想一想 圆的对称轴是任意一条经过圆心的直线圆的对称轴是任意一条经过圆心的直线, ,它有无数条对称轴它有无数条对称轴. .O O可利用折叠的方法即可解决上述问题可利用折叠的方法即可解决上述问题. .圆也是中心对称图形圆也是中心对称图形. .它的对称中心就是圆心它的对称中心就是圆心. .用旋转的方法即可解决这个问题用旋转的方法即可解决这个问题. .圆的对称性圆的对称性猜一猜猜一猜 请同学们观察屏幕上两个半径相等的圆。请回答：请同学们观察屏幕上两个半径相等的圆。请回答： 它们能重合吗？如果能重合，请将它们的圆心固定它们能重合吗？如果能重合，请将它们的

5、圆心固定在一起。在一起。 O然后将其中一个圆旋转任意一个角度，这时两个然后将其中一个圆旋转任意一个角度，这时两个圆还重合吗圆还重合吗 ?O归纳归纳 ：圆具有旋转不变性圆具有旋转不变性, ,即一个圆绕着它的即一个圆绕着它的圆心旋转任意一个角度，都能与原来的圆心旋转任意一个角度，都能与原来的圆重合。因此圆重合。因此, ,圆是中心对称圆形，对圆是中心对称圆形，对称中心为圆心称中心为圆心。圆的中心对称性是其旋。圆的中心对称性是其旋转不变性的特例转不变性的特例. .ABCDOAOBCODAOCBOD我们把我们把顶点顶点在在圆心圆心的的角叫做角叫做圆心角圆心角. 圆心角的概念圆心角的概念判别下列各图中的角

6、是不是圆心角，并说明理由。判别下列各图中的角是不是圆心角，并说明理由。2015.01弦心距：过圆心作弦的垂弦心距：过圆心作弦的垂线，圆心与垂足之间的距线，圆心与垂足之间的距离叫做弦心距离叫做弦心距CAFBEOD四量定理：在同圆或等圆中，如果两个四量定理：在同圆或等圆中，如果两个圆心角圆心角、两条两条弧弧、两条、两条弦，两条弦心距弦，两条弦心距中有一组量中有一组量 相等，那么它们所对应的其余各组量都分别相相等，那么它们所对应的其余各组量都分别相等。等。CABDEFO2015.01 1 1、如图，、如图，ABAB、CDCD是是OO的两条弦，的两条弦，OEOE、OFOF为为ABAB、CDCD的弦心距

7、的弦心距（1 1）如果）如果AB=CDAB=CD，那么，那么_，_， （2 2）如果）如果 ，那么，那么_，_， （3 3）如果）如果AOB=CODAOB=COD，那么，那么_，_ ,_ , （4 4）如果）如果OE=OFOE=OF，那么，那么_，_， CABDEFOOE=OFOE=OFAB= CDAB= CD AB= CDAB= CD AB=CDAB=CDAB=CDAB=CDAB= CDAB= CD AB= CDAB= CD AB=CDAB=CDOE=OFOE=OFOE=OFOE=OFAOB=CODAOB=CODAOB=CODAOB=CODAOB=CODAOB=COD练习练习2015.01证

8、明：证明：AB=ACAB=AC又又ACB=60ACB=60AB=BC=CAAB=BC=CA. .AOBAOBBOCBOCAOCAOC. .AB BCO例例1 1、如图、如图, , 在在OO中，中， , ACB=60, ACB=60. .求证：求证：AOB=BOC=AOC.AOB=BOC=AOC.AB= ACAB= AC AB= ACAB= AC 例题例题2015.01AOBCDE解：解：2 2、如图，、如图，ABAB是是O O 的直径，的直径，BC=CD=DEBC=CD=DE，COD=35COD=35，求求AOE AOE 的度数的度数 BC=CD=DE BC=CD=DE BOD=COD=DOE

9、=35 BOD=COD=DOE=35 AOE=180 AOE=180-3-33535 =75 =75练习练习 BEODAC例例2：（数学理解：（数学理解2）如图，在如图，在 O中，中，AB，CD是两是两条弦，条弦，OEAB，OFCD,重重足分别为足分别为E，F。CAFBEOD如果如果AOB=COD，那么，那么OE与与OF的大小的大小有什么关系？为什么？有什么关系？为什么？如果如果OE=OF那么那么AB与与CD的大小有什么关的大小有什么关系？为什么？系？为什么？ AOB与与 COD呢？呢？解：解：OE=OF，理由是：理由是：OEAB，OFCD，OA=OB，OC=OD，OEB=OFD=90,EOB

10、= AOB,FOD= CODAOB=COD，EOB=FOD，在在EOB和和FOD中，中，OEBOFD,EOBFOD , OBOD EOB FOD（AAS）OE=OF如图，在如图，在 O中，中，AB，CD是两条弦，是两条弦，OEAB，OFCD,重足分别为重足分别为E，F。CAFBEOD如果如果AOB=COD，那么，那么OE与与OF的的大小有什么关系？为什么？大小有什么关系？为什么？2121例例2：（数学理解：（数学理解2）解：解：AB=CD，AB=CD，AOB=COD，理由是：理由是：OEAB，OFCDOEB=OFD=90在在RtBEO和和RtDFO中，中，OBOD,OEOF RtBEO RtD

11、FO（HL）BE=DF，由垂径定理得：由垂径定理得：AB=2BE，CD=2DF，AB=CD，AB=CD，AOB=COD 如图，在如图，在 O中，中，AB，CD是两条弦，是两条弦，OEAB，OFCD,重足分别为重足分别为E，F。CAFBEOD如果如果OE=OF那么那么AB与与CD的大小有什的大小有什么关系？么关系？ AB与与CD的大小有什么关系？的大小有什么关系？为什么？为什么？ AOB与与 COD呢？呢？例例2：（数学理解：（数学理解2）随堂练习随堂练习2.利用一个圆及其若干条弦分别设计出符合条件的图案：利用一个圆及其若干条弦分别设计出符合条件的图案：（1）是轴对称图形但不是中心对称图形）是轴

12、对称图形但不是中心对称图形（2）是中心对称图形但不是轴对称图形）是中心对称图形但不是轴对称图形（3）既是轴对称图形又是中心对称图形）既是轴对称图形又是中心对称图形随堂练习随堂练习OA BC知识技能知识技能1.如图，如图，A、B、C、D是是 O上的四点，上的四点，AB=DC，ABC与与DCB全等吗？为什么？全等吗？为什么？OBADC数学理解数学理解OA BCD练习练习 如图如图, O中，中，ABCD. （1）求证：）求证： AOC = BOD （2）求证：）求证：AC=BDODCAB你能得出什么结论？你能得出什么结论？在同一个圆中，在同一个圆中，两条平行弦所夹的弦相等，所夹的弧相等。两条平行弦所夹的弦相等，所夹的弧相等。211.1.圆是轴对称图形圆是轴对称图形. . 圆的对称轴是任意一条经过圆心的直线圆的对称轴是任意一条经过圆心的直线, ,它有无数条对称轴它有无数条对称轴. .2.2.圆也是中心对称图形圆也是中心对称图形. .它的对称中心就是圆心它的对称中心就是圆心. .课时小结课时小结4.定