复数的几何意义课件(公开课)

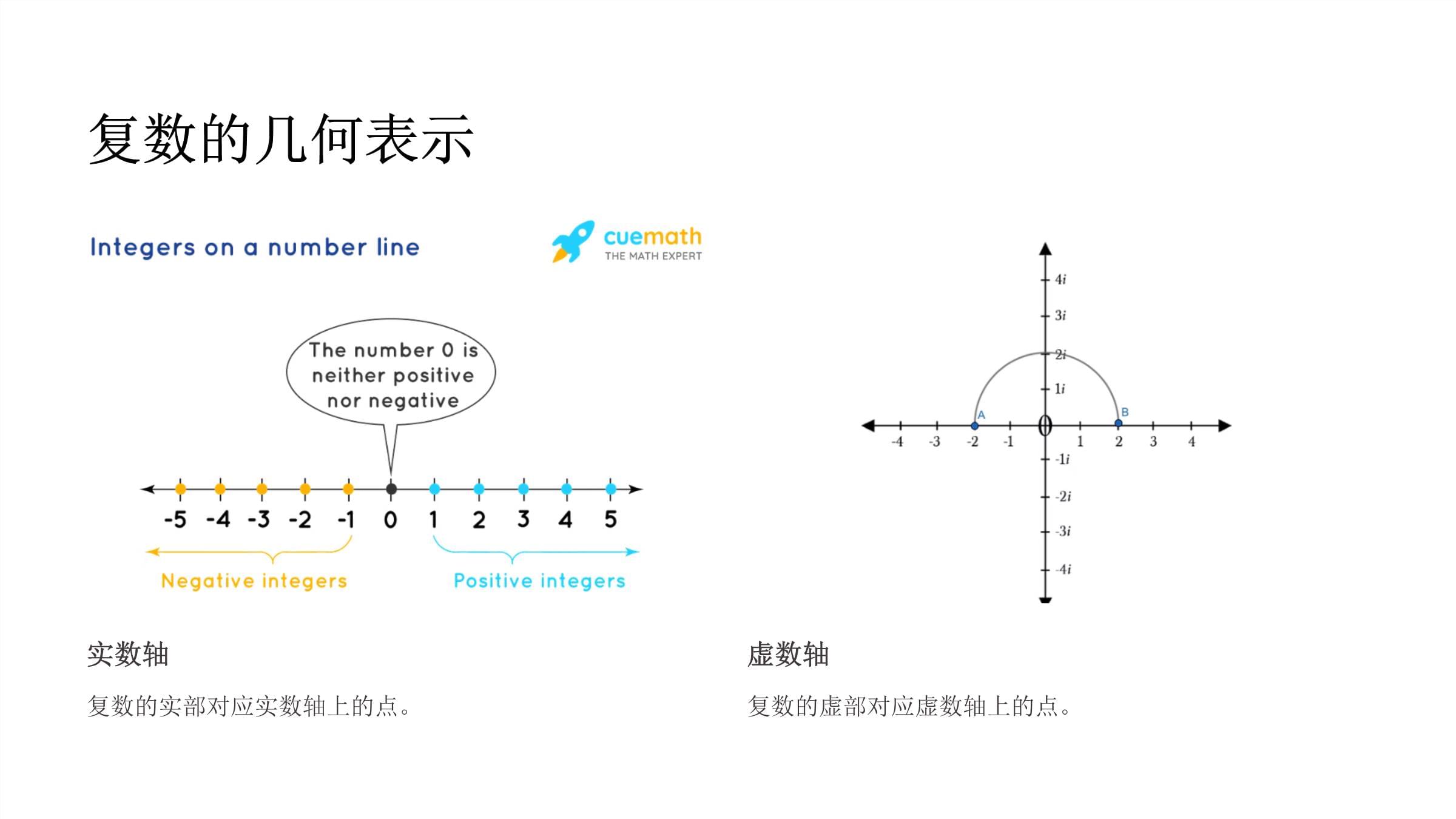
复数的几何意义本课件将探索复数的几何意义，并探讨其在数学、物理和其他领域中的应用。复数的概念回顾实数在数轴上可以表示的数，例如1,2,3,-1,-2,-3,0,π,√2等。虚数单位定义为-1的平方根，记为i，即i^2=-1。复数形如a+bi的数，其中a和b是实数，i是虚数单位。复数的性质加法复数的加法满足交换律和结合律。类似于向量加法，复数加法可以被视为在复平面上将两个复数的向量进行几何叠加。乘法复数的乘法同样满足交换律和结合律。乘法运算可以被视为在复平面上旋转和伸缩，旋转角度由两个复数的辐角之和决定，伸缩比例由两个复数的模长之积决定。单位元复数1是加法运算的单位元，复数1是乘法运算的单位元。逆元每个非零复数都有一个加法逆元，每个非零复数都有一个乘法逆元。复数的加法和乘法加法复数的加法遵循向量加法的法则，即对应实部和虚部相加。乘法复数的乘法遵循分配律，将两个复数相乘，并将结果化简为标准形式。复数的几何表示实数轴复数的实部对应实数轴上的点。虚数轴复数的虚部对应虚数轴上的点。模和辐角1模复数的模表示复数在复平面上的长度，也称为绝对值.2辐角复数的辐角是指复数与实轴正方向所成的角度.复数的极坐标形式1模长复数到原点的距离2辐角复数与实轴的夹角模长和辐角的计算模长使用勾股定理计算复数在复平面上的距离辐角使用反正切函数计算复数与实轴之间的角度模长公式RealPartImaginaryPart复数z=a+bi的模长|z|等于z在复平面上的对应点到原点的距离，即|z|=√(a²+b²).辐角公式1正切复数的辐角可以通过正切函数来计算2范围辐角通常在0到2π之间3象限根据复数所在的象限，需要调整辐角的取值4特殊情况当实部或虚部为0时，辐角取特殊值复数的乘法和除法1复数乘法$(a+bi)(c+di)=(ac-bd)+(ad+bc)i$2复数除法$\frac{a+bi}{c+di}=\frac{(a+bi)(c-di)}{(c+di)(c-di)}=\frac{ac+bd}{c^2+d^2}+\frac{bc-ad}{c^2+d^2}i$复数乘法的几何意义复数乘法可以理解为旋转和平移的组合。将一个复数乘以另一个复数，相当于将第一个复数在复平面上绕原点旋转一个角度，然后按比例缩放。旋转角度等于第二个复数的辐角，缩放比例等于第二个复数的模长。复数除法的几何意义复数除法可以理解为将一个复数旋转并缩放另一个复数的过程。设两个复数为*z1*和*z2*，它们的模长分别为*|z1|*和*|z2|*，辐角分别为*θ1*和*θ2*，则它们的商*z1/z2*的模长为*|z1|/|z2|*，辐角为*θ1-θ2*。因此，复数除法可以看作是将*z1*旋转*θ2*度，并缩放*1/|z2|*倍得到*z1/z2*。复数的幂运算1基本定义复数的幂运算类似于实数的幂运算，将复数自身乘以其本身多次。2公式对于复数z和正整数n，z的n次幂定义为z^n=z*z*...*z（n个z相乘）。3几何意义复数幂运算在复平面上表现为模长变化和辐角的倍增。指数形式下的幂运算1复数的指数形式使用欧拉公式，可以将复数表示为指数形式：z=re^(iθ)。2幂运算复数的幂运算遵循指数的性质：(re^(iθ))^n=r^ne^(inθ)。3几何解释复数的幂运算在复平面上对应着旋转和伸缩，旋转角度为nθ，伸缩倍数为r^n。复平面上的幂运算几何表示复数的乘法对应着复平面上旋转和缩放的复合变换。幂运算复数的幂运算可以通过重复乘法来实现，在复平面上体现为多次旋转和缩放。复数与平面几何复数的几何表示复数可以通过平面上的点来表示，横坐标代表实部，纵坐标代表虚部。复数的加减法复数的加减法可以看作向量加减法，在平面上的几何意义是平行四边形法则。复数的乘法复数的乘法可以通过模长和辐角的运算来实现，在平面上的几何意义是旋转和伸缩。复数表示的平面几何元素点每个复数对应平面上的一个点。例如，复数z=a+bi对应点(a,b)。向量复数还可以表示向量。复数z=a+bi表示从原点到点(a,b)的向量。直线用复数方程可以表示平面上的直线。例如，过点z1且方向向量为z2的直线方程为z=z1+t*z2，其中t为参数。圆圆可以用复数方程表示。例如，以z0为圆心，半径为r的圆方程为|z-z0|=r。复数在几何变换中的应用平移变换复数加法可以表示平移变换，例如z+a表示将复数z平移a个单位。旋转变换复数乘法可以表示旋转变换，例如z*a表示将复数z绕原点旋转arg(a)角度并伸缩|a|倍。伸缩变换复数乘以一个实数可以表示伸缩变换，例如z*k表示将复数z伸缩k倍。复数的平方根平方根的定义对于一个复数z，如果存在另一个复数w，满足w^2=z，则称w为z的平方根。平方根的性质每个非零复数都有两个平方根，这两个平方根互为相反数。平方根的定义1定义对于一个非负实数a，若存在一个实数b，使得b²=a，则称b为a的平方根。2符号用符号√a表示a的非负平方根。3性质每个非负实数都有两个平方根，一个是正数，另一个是负数。平方根的性质唯一性每个复数有两个平方根，它们互为相反数加法性质复数的平方根的加法满足一定规律乘法性质复数的平方根的乘法也满足一定规律三角函数与复数1复数的三角形式复数可以表示为三角形式，即用模长和辐角来表示复数。2三角函数的表示三角函数可以通过复数的模长和辐角来表示，例如，余弦函数可以表示为复数的实部，正弦函数可以表示为复数的虚部。3复数与三角函数的联系复数和三角函数之间存在密切的联系，通过复数的三角形式可以更直观地理解三角函数的性质和应用。复数表示三角函数复数可以用来表示三角函数，例如：cosθ+isinθ表示单位圆上角度为θ的点。这个复数的模长为1，辐角为θ，因此它的实部为cosθ，虚部为sinθ。三角函数在复平面中的应用单位圆复平面上的单位圆可以用来表示三角函数。欧拉公式欧拉公式将三角函数与指数函数联系起来，为复平面上的运算提供了便捷的方法。几何变换三角函数可以用来描述复平面上的旋转，例如：旋转一个复数。练习与总结1课堂练习巩固学习内容2复数几何意义总结回顾学习要点练习是检验学习成果的关键，帮助学生巩固所学知识并发现不足。总结复数几何意义，加深对复数的理解和应用。课堂练习复数加法计算(2+3i)+(4-5i)。复数乘法计算(1+2