142乘法公式（讲练）-2022-2023学年八年级数学上册重要考点(人教版)（原卷版）

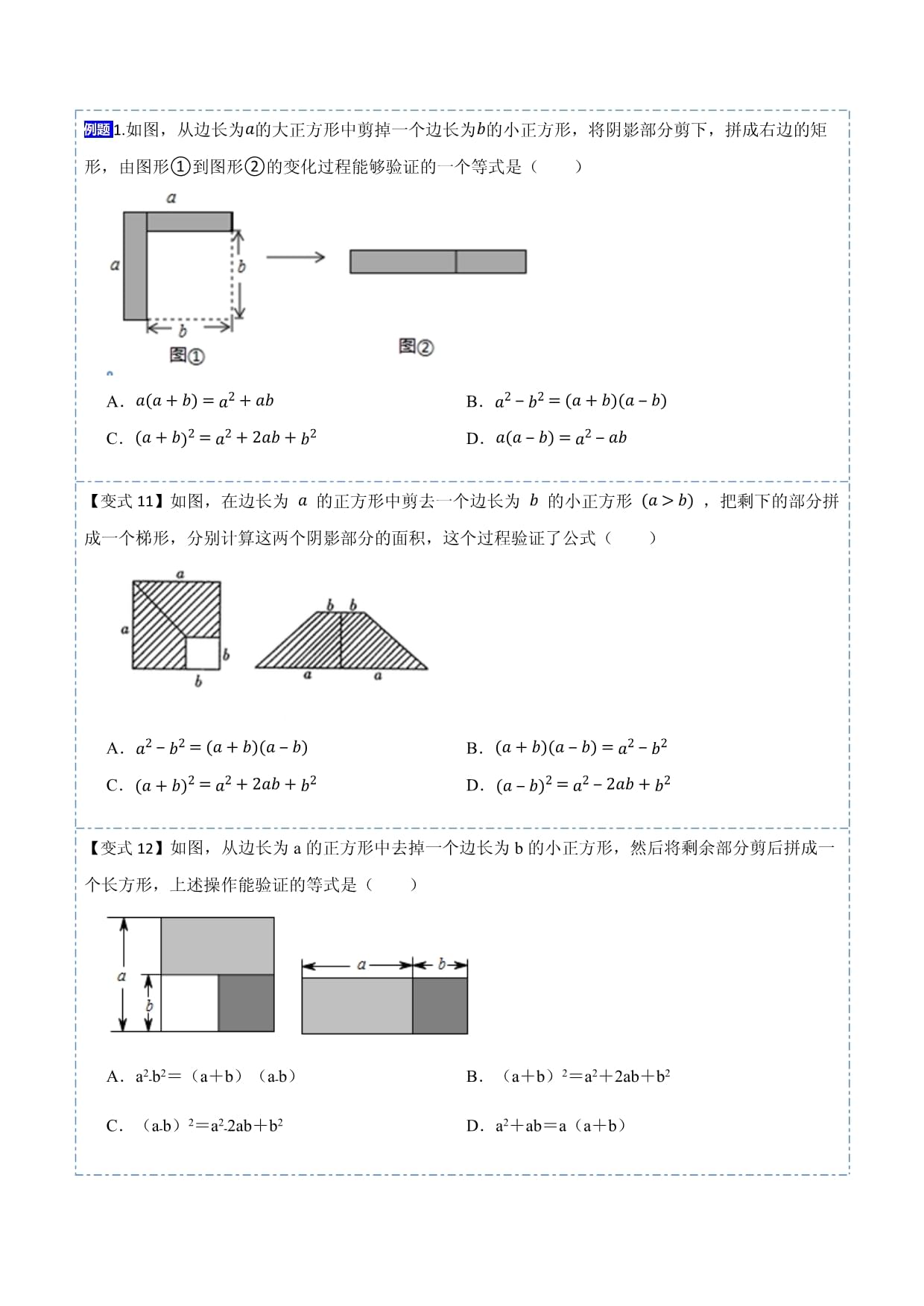
14.2乘法公式平方差公式平方差公式：两个数的和与这两个数的差的积，等于这两个数的平方差.注意：在这里，既可以是具体数字，也可以是单项式或多项式.抓住公式的几个变形形式利于理解公式.但是关键仍然是把握平方差公式的典型特征：既有相同项，又有“相反项”，而结果是“相同项”的平方减去“相反项”的平方.常见的变式有以下类型：（1）位置变化：如利用加法交换律可以转化为公式的标准型（2）系数变化：如（3）指数变化：如（4）符号变化：如（5）增项变化：如（6）增因式变化：如题型1：平方差公式用面积探究公式1.如图，从边长为a的大正方形中剪掉一个边长为b的小正方形，将阴影部分剪下，拼成右边的矩形，由图形①到图形②的变化过程能够验证的一个等式是（）A．a(a+bC．(a+b)【变式11】如图，在边长为a的正方形中剪去一个边长为b的小正方形(a>bA．a2-b2C．(a+b)【变式12】如图，从边长为a的正方形中去掉一个边长为b的小正方形，然后将剩余部分剪后拼成一个长方形，上述操作能验证的等式是（）A．a2﹣b2＝（a＋b）（a﹣b） B．（a＋b）2＝a2＋2ab＋b2C．（a﹣b）2＝a2﹣2ab＋b2 D．a2＋ab＝a（a＋b）题型2：平方差公式识别2.下列式子可用平方差公式计算的是（）A．(a+b)(a−b) B．(a−b)(b−a)C．(a+2b)(2b+a) D．(y2x)(2x+y)【变式21】下列多项式中能用平方差公式分解因式的是（）A．﹣a2﹣b2 B．x2+（﹣y）2C．（﹣x）2+（﹣y）2 D．﹣m2+1【变式22】下列两个多项式相乘，哪些可用平方差公式，哪些不能?能用平方差公式计算的，写出计算结果．(1)；(2)；(3)；(4)；(5)；(6)．题型3：平方差公式计算3.计算（4＋x）（x－4）的结果是（）A．x2-16 B．x2+16 C．【变式31】计算(-2a-3A．4a2-9C．-4a2-【变式32】计算：（1）；（2）；（3）．题型4：平方差公式混合运算及简便运算4.2、计算：(1)59.9×60.1；(2)102×98．【变式41】计算：（1）991×1009（2）用公式进行简便计算.20222﹣2023×2021．（3）(【变式42】阅读并完成下列各题：通过学习，同学们已经体会到灵活运用整式乘法公式给计算和化简带来的方便、快捷．相信通过下面材料的学习、探究，会使你大开眼界，并获得成功的喜悦．【例】用简便方法计算995×1005．解：995×1005=（1000﹣5）（1000+5）①=10002﹣52②=999975．（1）例题求解过程中，第②步变形是利用（填乘法公式的名称）；（2）用简便方法计算：9×11×101×10001；题型5：平方差公式巧用公式计算5.计算：（2+1）（22+1）（24+1）…（232+1）+1．【变式51】某同学在计算3（4+1）（42+1）时，把3写成4﹣1后，发现可以连续运用两数和乘以这两数差公式计算：3（4+1）（42+1）=（4﹣1）（4+1）（42+1）=（42﹣1）（42+1）=162﹣1=255．请借鉴该同学的经验，计算：(1+12完全平方公式完全平方公式：两数和(差)的平方等于这两数的平方和加上（减去）这两数乘积的两倍.注意：公式特点：左边是两数的和（或差）的平方，右边是二次三项式，是这两数的平方和加（或减）这两数之积的2倍.以下是常见的变形（重要）：题型6：完全平方公式用面积探究公式6.如图，根据计算正方形ABCD的面积，可以说明下列哪个等式成立（）A．（a﹣b）2=a2﹣2ab+b2 B．（a+b）2=a2+2ab+b2C．（a+b）（a﹣b）=a2﹣b2 D．a（a﹣b）=a2﹣ab【变式61】通过计算几何图形的面积可表示一些代数恒等式，下图可表示的代数恒等式是（）A．(a-b)C．(a+b)【变式62】如图，将图1中阴影部分拼成图2，根据两个图形中阴影部分的关系，可以验证下列哪个计算公式（）A．（a﹣b）2＝a2﹣2ab+b2 B．（a+b）2＝a2+2ab+b2C．（a﹣b）2＝（a+b）2﹣4ab D．（a+b）（a﹣b）＝a2﹣b2题型7：完全平方公式识别7.下列各式中，能用完全平方公式计算的是（）A．(x-y)(C．(x-y)(-【变式71】下列各式中，能用完全平方公式计算的是（）A．（a﹣b）（﹣b﹣a） B．（﹣n2﹣m2）（m2+n2）C．(-12p+q)(q+12p) D【变式72】下列式子满足完全平方公式的是（）A．（3x﹣y）（﹣y﹣3x） B．（3x﹣y）（3x+y）C．（﹣3x﹣y）（y﹣3x） D．（﹣3x﹣y）（y+3x）题型8：完全平方公式计算8.下列计算正确的是（）A．  B． C． D． 【变式81】下列运算正确的是（）A．(x+y)2=x2+y2 B．(xy)2=x2+2xy+y2C．(x+y)2=x2+y2+2xy D．(xy)2=x2xy+y2【变式82】计算：(1)；(2)；(3)；(4)．题型9：完全平方公式混合运算9.简便计算：（1）982（2）20202﹣4040×2019+20192（3）计算（2x+y）2﹣（y﹣2x）2【变式91】计算：（1）(2（2）（x+2）（x﹣2）﹣（x+1x）（3）(x+2)（4）9（a－1）2－（3a＋2）（3a－2）；【变式92】（1）简算：20182－4036×2017＋20172（2）计算(题型10：完全平方公式公式变形求代数式的值10.a+b=5，ab=-2，求【变式101】已知(m+n)2=9,(【变式102】已知(a+b)2=60，(a-b)2添括号法则添括号时，如果括号前面是正号，括到括号里的各项都不变符号；如果括号前面是负号，括到括号里的各项都改变符号.注意：添括号与去括号是互逆的，符号的变化也是一致的，可以用去括号法则检查添括号是否正确.题型11：完全平方公式添括号11.运用乘法公式计算：（1）；（2）．【变式111】运用乘法公式计算：(1)；(2)；(3)；(4)．题型12：完全平方公式构造完全平方公式12.若x，y是等腰三角形的两条边，且满足4x2+17y【变式121】已知a，b，c是△ABC的三边长，且满足a2+b2﹣4a﹣8b+20=0，c=3cm，求△ABC的周长.【变式122】在△ABC中，BC＝a，AC＝b，AB＝c，且满足a2+b2+12c2＝ac+bc，试判定题型13：用乘法公式证明整除问题13.求证：对任意整数n,整式（3n+1）（3n1）（3n）（3+n）的值都能被10整除．【变式131】求证：对任意自然数n,式子（n1）（n+1）（n5）（n7）的值都能被12整除．【变式132】设两个连续奇数为2n1和2n+1，则这两个数的平方差（较大的减去较小的）是否一定被8整除？请说明理由．题型14：乘法公式在几何中的应用14.图①是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后按图②的形状拼成一个正方形．（1）将图②中的阴影部分面积用2种方法表示可得一个等式，求等式。（2）若m+2n=7，mn=3，利用（1）的结论求m﹣2n的值．【变式141】用4个相同的小长方形与1个小正方形密铺而成的大正方形图案如图所示，已知大正方形的面积为36，小正方形的面积为4，用x、y（x＞y）分别表示小长方形的两边长．

（1）求x2+y2的值；（2）求xy的值．【变式142】我们知道，对于一个图形，通过两种不同的方法计算它的面积，可以得到一个等式．例如图1可以得到(a+（1）根据图2，完成数学等式：(2a)2=（2）观察图3，写出图3中所表示的等式：＝.（3）若a=7x-5、b=-4x+2、c=-3x+4，且题型15：乘法公式与化简求值15.先化简，再求值：(a+b)(a【变式151】先化简，再求值：(a+3)2(a+1)(a1)2(2a+4)，其中a=1【变式152】先化简，再求值：(2x+y)2-(2x+y)(2题型16：用乘法公式解规律探究题16.阅读下面内容回答问题：

（x1）（x+1）=x21

（x1）（x2+x+1）=x31

（x1）（x3+x2+x+1）=x41

（x1）（x4+x3+x2+x+1）=x51

……

（1）按这样的规律写出第6个式子用你找出的规律计算1+2+22+23+24+25+26的值【变式161】观察下面各式规律：12+（1×2）2+22=（1×2+1）2；22+（2×3）2+32=（2×3+1）2；32+（3×4）2+42=（3×4+1）2…写出第n行的式子，并证明你的结论．【变式162】你能很快计算出19952吗？

（1）通过计算，探索规律：

152=225=100×（1+1）+25，

252=625=100×2×（2+1）+25，

352=1225=100×3×（3+1）+25，

452=2025=100×4×（4+1）+25，

…

752=5625=852=7225=…

（2）观察以上结果，归纳、猜想得（10n+5）2=。并运用整式运算的知识给予说明．

（3）利用上述结论，计算19952．一、单选题1．下面计算正确是（）A．x3+4x3＝5x6 B．a2•a3＝a6C．（﹣2x3）4＝16x12 D．（x+2y）（x﹣2y）＝x2﹣2y22．下列运算正确的是（）A．2x+3x=6C．(-x3)23．下列计算正确的是（）A．(a+b)C．4a3⋅34．若a、b、c为一个三角形的三条边，则代数式a-A．一定为正数 B．一定为负数C．可能为正数，也可能为负数 D．可能为零5．下列运算正确的是（）A．2a2﹣a2=2 B．2a•3a=6a2C．（a﹣b）2=a2﹣b2 D．a6÷a2=a36．下列多项式的乘法中，不能用平方差公式计算的是()A．(4x-3yC．(a+b-二、填空题7．计算①(2x+y)(2x-y)=8．已知(a+b)2=49，a2+9．已知实数a、b满足ab=3，ab=2，则a²+b²的值为。10．已知关于x的二次三项式x2+2mx﹣m2+4是一个完全平方式，则m的值为三、计算题11．计算（1）a2b(ab4b2)；（2）(2x+4)(x2)；（3）(2xy)2(2x)2；（4）598×602（用简便方法计算）.四、解答题12．计算：（13．光明村正在进行绿地改造，原有一正方形绿地，现将它每边都增加3米，面积则增加了63平方米，问原绿地的边长为多少？原绿地的面积又为多少？五、综合题14．把几个图形拼成一个新的图形，再通过图形面积的计算，常常可以得到一些有用的式子，或可以求出一些不规则图形的面积．（1）如图1，是将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形，试用不同的方法计算这个图形的面积，你能发现什么结论，请写出来．（2）如图2，是将两个边长分别为a和b的正方形拼在一起，B、C、G三点在同一直线上，连接BD和B