广东省香洲区四校联考2021-2022学年中考数学最后冲刺浓缩卷含解析

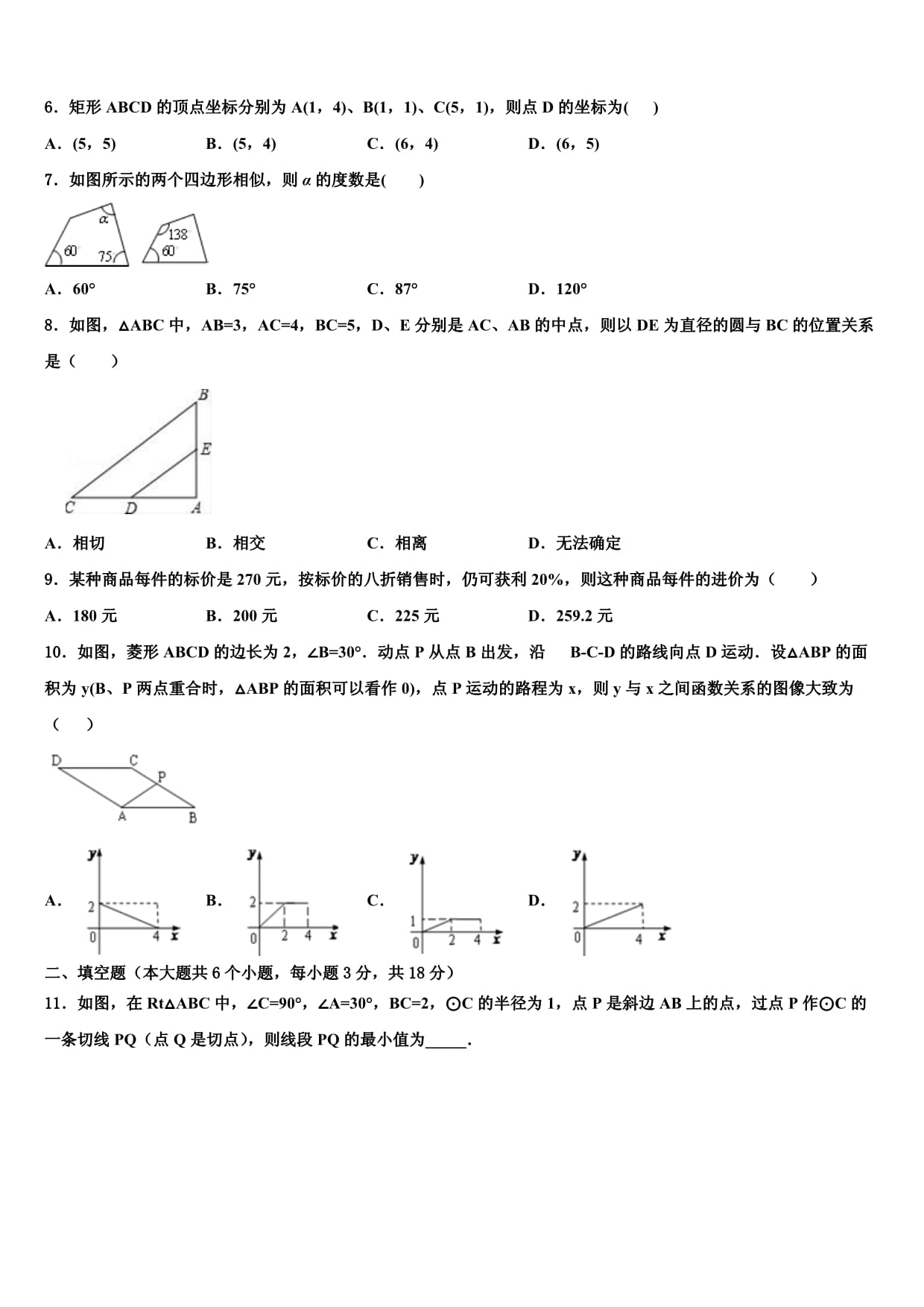
广东省香洲区四校联考2021-2022学年中考数学最后冲刺浓缩精华卷注意事项1．考试结束后，请将本试卷和答题卡一并交回．2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．一、选择题（共10小题，每小题3分，共30分）1．下列图形中，是正方体表面展开图的是（）A． B． C． D．2．tan60°的值是()A． B． C． D．3．小明为今年将要参加中考的好友小李制作了一个（如图）正方体礼品盒，六面上各有一字，连起来就是“预祝中考成功”，其中“预”的对面是“中”，“成”的对面是“功”，则它的平面展开图可能是（）A． B． C． D．4．如图是由若干个相同的小正方体搭成的一个几何体的主视图和俯视图，则所需的小正方体的个数最少是（）A． B． C． D．5．下列运算正确的是()A． B． C． D．6．矩形ABCD的顶点坐标分别为A(1，4)、B(1，1)、C(5，1)，则点D的坐标为()A．(5，5) B．(5，4) C．(6，4) D．(6，5)7．如图所示的两个四边形相似，则α的度数是()A．60° B．75° C．87° D．120°8．如图，△ABC中，AB=3，AC=4，BC=5，D、E分别是AC、AB的中点，则以DE为直径的圆与BC的位置关系是（）A．相切 B．相交 C．相离 D．无法确定9．某种商品每件的标价是270元，按标价的八折销售时，仍可获利20%，则这种商品每件的进价为（）A．180元 B．200元 C．225元 D．259.2元10．如图，菱形ABCD的边长为2，∠B=30°．动点P从点B出发，沿B-C-D的路线向点D运动．设△ABP的面积为y(B、P两点重合时，△ABP的面积可以看作0)，点P运动的路程为x，则y与x之间函数关系的图像大致为（）A． B． C． D．二、填空题（本大题共6个小题，每小题3分，共18分）11．如图，在Rt△ABC中，∠C=90°，∠A=30°，BC=2，⊙C的半径为1，点P是斜边AB上的点，过点P作⊙C的一条切线PQ（点Q是切点），则线段PQ的最小值为_____．12．如图，已知△ABC和△ADE均为等边三角形，点OAC的中点，点D在A射线BO上，连接OE，EC，若AB＝4，则OE的最小值为_____．13．若关于x的一元二次方程x2﹣2x+m=0有实数根，则m的取值范围是．14．分解因式：m2n﹣2mn+n=．15．如图，已知⊙O1与⊙O2相交于A、B两点，延长连心线O1O2交⊙O2于点P，联结PA、PB，若∠APB=60°,AP=6，那么⊙O2的半径等于________．16．三人中有两人性别相同的概率是_____________.三、解答题（共8题，共72分）17．（8分）当x取哪些整数值时，不等式与4﹣7x＜﹣3都成立？18．（8分）如图，▱ABCD的对角线AC，BD相交于点O．E，F是AC上的两点，并且AE=CF，连接DE，BF．（1）求证：△DOE≌△BOF；（2）若BD=EF，连接DE，BF．判断四边形EBFD的形状，并说明理由．19．（8分）如图，已知直线l与⊙O相离，OA⊥l于点A，交⊙O于点P，OA=5，AB与⊙O相切于点B，BP的延长线交直线l于点C.（1）求证：AB=AC；（2）若，求⊙O的半径.20．（8分）有A，B两个黑布袋，A布袋中有两个完全相同的小球，分别标有数字1和1．B布袋中有三个完全相同的小球，分别标有数字﹣1，﹣1和﹣2．小明从A布袋中随机取出一个小球，记录其标有的数字为x，再从B布袋中随机取出一个小球，记录其标有的数字为y，这样就确定点Q的一个坐标为（x，y）．（1）用列表或画树状图的方法写出点Q的所有可能坐标；（1）求点Q落在直线y=﹣x﹣1上的概率．21．（8分）已知：二次函数图象的顶点坐标是(3，5)，且抛物线经过点A(1，3)．(1)求此抛物线的表达式；(2)如果点A关于该抛物线对称轴的对称点是B点，且抛物线与y轴的交点是C点，求△ABC的面积．22．（10分）4月9日上午8时，2017徐州国际马拉松赛鸣枪开跑，一名岁的男子带着他的两个孩子一同参加了比赛，下面是两个孩子与记者的对话：根据对话内容，请你用方程的知识帮记者求出哥哥和妹妹的年龄.23．（12分）某商场计划从厂家购进甲、乙、丙三种型号的电冰箱80台，其中甲种电冰箱的台数是乙种电冰箱台数的2倍．具体情况如下表：甲种乙种丙种进价（元/台）120016002000售价（元/台）142018602280经预算，商场最多支出132000元用于购买这批电冰箱．（1）商场至少购进乙种电冰箱多少台？（2）商场要求甲种电冰箱的台数不超过丙种电冰箱的台数．为获得最大利润，应分别购进甲、乙、丙电冰箱多少台？获得的最大利润是多少？24．试探究：小张在数学实践活动中，画了一个△ABC，∠ACB＝90°，BC＝1，AC＝2，再以点B为圆心，BC为半径画弧交AB于点D，然后以A为圆心，AD长为半径画弧交AC于点E，如图1，则AE＝；此时小张发现AE2＝AC•EC，请同学们验证小张的发现是否正确．拓展延伸：小张利用图1中的线段AC及点E，构造AE＝EF＝FC，连接AF，得到图2，试完成以下问题：（1）求证：△ACF∽△FCE；（2）求∠A的度数；（3）求cos∠A的值；应用迁移：利用上面的结论，求半径为2的圆内接正十边形的边长．

参考答案一、选择题（共10小题，每小题3分，共30分）1、C【解析】

利用正方体及其表面展开图的特点解题．【详解】解：A、B、D经过折叠后，下边没有面，所以不可以围成正方体，C能折成正方体．故选C．【点睛】本题考查了正方体的展开图，解题时牢记正方体无盖展开图的各种情形．2、A【解析】

根据特殊角三角函数值，可得答案．【详解】tan60°=故选：A．【点睛】本题考查了特殊角三角函数值，熟记特殊角三角函数值是解题关键．3、C【解析】

正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点对各选项分析判断后利用排除法求解：【详解】正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点对各选项分析判断后利用排除法求解：A、“预”的对面是“考”，“祝”的对面是“成”，“中”的对面是“功”，故本选项错误；B、“预”的对面是“功”，“祝”的对面是“考”，“中”的对面是“成”，故本选项错误；C、“预”的对面是“中”，“祝”的对面是“考”，“成”的对面是“功”，故本选项正确；D、“预”的对面是“中”，“祝”的对面是“成”，“考”的对面是“功”，故本选项错误．故选C【点睛】考核知识点：正方体的表面展开图.4、B【解析】

主视图、俯视图是分别从物体正面、上面看，所得到的图形．【详解】综合主视图和俯视图，底层最少有个小立方体，第二层最少有个小立方体，因此搭成这个几何体的小正方体的个数最少是个．故选：B．【点睛】此题考查由三视图判断几何体，解题关键在于识别图形5、D【解析】

根据幂的乘方：底数不变，指数相乘．合并同类项即可解答.【详解】解：A、B两项不是同类项，所以不能合并，故A、B错误，C、D考查幂的乘方运算，底数不变，指数相乘．,故D正确；【点睛】本题考查幂的乘方和合并同类项，熟练掌握运算法则是解题的关键.6、B【解析】

由矩形的性质可得AB∥CD，AB=CD，AD=BC，AD∥BC，即可求点D坐标．【详解】解：∵四边形ABCD是矩形

∴AB∥CD，AB=CD，AD=BC，AD∥BC，

∵A（1，4）、B（1，1）、C（5，1），

∴AB∥CD∥y轴，AD∥BC∥x轴

∴点D坐标为（5，4）

故选B．【点睛】本题考查了矩形的性质，坐标与图形性质，关键是熟练掌握这些性质.7、C【解析】【分析】根据相似多边形性质：对应角相等.【详解】由已知可得：α的度数是：360〫-60〫-75〫-138〫=87〫故选C【点睛】本题考核知识点：相似多边形.解题关键点：理解相似多边形性质.8、B【解析】

首先过点A作AM⊥BC，根据三角形面积求出AM的长，得出直线BC与DE的距离，进而得出直线与圆的位置关系．【详解】解：过点A作AM⊥BC于点M，交DE于点N，∴AM×BC=AC×AB，∴AM===2.1．∵D、E分别是AC、AB的中点，∴DE∥BC，DE=BC=2.5，∴AN=MN=AM，∴MN=1.2．∵以DE为直径的圆半径为1.25，∴r=1.25＞1.2，∴以DE为直径的圆与BC的位置关系是：相交．故选B．【点睛】本题考查了直线和圆的位置关系，利用中位线定理得出BC到圆心的距离与半径的大小关系是解题的关键．9、A【解析】

设这种商品每件进价为x元，根据题中的等量关系列方程求解.【详解】设这种商品每件进价为x元，则根据题意可列方程270×0.8－x＝0.2x，解得x＝180.故选A.【点睛】本题主要考查一元一次方程的应用，解题的关键是确定未知数，根据题中的等量关系列出正确的方程.10、C【解析】

先分别求出点P从点B出发，沿B→C→D向终点D匀速运动时，当0＜x≤2和2＜x≤4时，y与x之间的函数关系式，即可得出函数的图象．【详解】由题意知，点P从点B出发，沿B→C→D向终点D匀速运动，则

当0＜x≤2，y=x，

当2＜x≤4，y=1，

由以上分析可知，这个分段函数的图象是C．

故选C．二、填空题（本大题共6个小题，每小题3分，共18分）11、．【解析】

当PC⊥AB时，线段PQ最短；连接CP、CQ，根据勾股定理知PQ2=CP2﹣CQ2，先求出CP的长，然后由勾股定理即可求得答案．【详解】连接CP、CQ；如图所示：∵PQ是⊙C的切线，∴CQ⊥PQ，∠CQP=90°，根据勾股定理得：PQ2=CP2﹣CQ2，∴当PC⊥AB时，线段PQ最短．∵在Rt△ACB中，∠A=30°，BC=2，∴AB=2BC=4，AC=2，∴CP===，∴PQ==，∴PQ的最小值是．故答案为：．【点睛】本题考查了切线的性质以及勾股定理的运用；注意掌握辅助线的作法，注意当PC⊥AB时，线段PQ最短是关键．12、1【解析】

根据等边三角形的性质可得OC＝AC，∠ABD＝30°，根据“SAS”可证△ABD≌△ACE，可得∠ACE＝30°＝∠ABD，当OE⊥EC时，OE的长度最小，根据直角三角形的性质可求OE的最小值．【详解】解：∵△ABC的等边三角形，点O是AC的中点，∴OC＝AC，∠ABD＝30°∵△ABC和△ADE均为等边三角形，∴AB＝AC，AD＝AE，∠BAC＝∠DAE＝60°，∴∠BAD＝∠CAE，且AB＝AC，AD＝AE，∴△ABD≌△ACE（SAS）∴∠ACE＝30°＝∠ABD当OE⊥EC时，OE的长度最小，∵∠OEC＝90°，∠ACE＝30°∴OE最小值＝OC＝AB＝1，故答案为1【点睛】本题考查了全等三角形的判定和性质，等边三角形的性质，熟练运用全等三角形的判定是本题的关键．13、m≤1．【解析】试题分析：由题意知，△=4﹣4m≥0，∴m≤1．故答案为m≤1．考点：根的判别式．14、n（m﹣1）1．【解析】

先提取公因式n后，再利用完全平方公式分解即可【详解】m1n﹣1mn+n=n（m1﹣1m+1）=n（m﹣1）1．故答案为n（m﹣1）1．15、2【解析】

由题意得出△ABP为等边三角形，在Rt△ACO2中，AO2=即可.【详解】由题意易知：PO1⊥AB，∵∠APB=60°∴△ABP为等边三角形，AC=BC=3∴圆心角∠AO2O1=60°∴在Rt△ACO2中，AO2==2.故答案为2.【点睛】本题考查的知识点是圆的性质，解题的关键是熟练的掌握圆的性质.16、1【解析】分析：由题意和生活实际可知：“三个人中，至少有两个人的性别是相同的”即可得到所求概率为1.详解：∵三人的性别存在以下可能：（1）三人都是“男性”；（2）三人都是“女性”；（3）三人的性别是“2男1女”；（4）三人的性别是“2女1男”，∴三人中至少有两个人的性别是相同的，∴P（三人中有二人性别相同）=1.点睛：列出本题中所有的等可能结果是解题的关键.三、解答题（共8题，共72分）17、2，1【解析】

根据题意得出不等式组，解不等式组求得其解集即可．【详解】根据题意得，解不等式①，得：x≤1，解不等式②，得：x＞1，则不等式组的解集为1＜x≤1，∴x可取的整数值是2，1．【点睛】本题考查了解不等式组的能力，根据题意得出不等式组是解题的关键．18、（2）证明见解析；（2）四边形EBFD是矩形．理由见解析.【解析】分析：（1）根据SAS即可证明；（2）首先证明四边形EBFD是平行四边形，再根据对角线相等的平行四边形是矩形即可证明；【解答】（1）证明：∵四边形ABCD是平行四边形，∴OA=OC，OB=OD，∵AE=CF，∴OE=OF，在△DEO和△BOF中，，∴△DOE≌△BOF．（2）结论：四边形EBFD是矩形．理由：∵OD=OB，OE=OF，∴四边形EBFD是平行四边形，∵BD=EF，∴四边形EBFD是矩形．点睛：本题考查平行四边形的性质，全等三角形的判定和性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．19、（1）证明见解析；（2）1．【解析】

（1）由同圆半径相等和对顶角相等得∠OBP=∠APC，由圆的切线性质和垂直得∠ABP+∠OBP=90°和∠ACB+∠APC=90°，则∠ABP=∠ACB，根据等角对等边得AB=AC；（2）设⊙O的半径为r，分别在Rt△AOB和Rt△ACP中根据勾股定理列等式，并根据AB=AC得52﹣r2=（2）2﹣（5﹣r）2，求出r的值即可．【详解】解：（1）连接OB，∵OB=OP，∴∠OPB=∠OBP，∵∠OPB=∠APC，∴∠OBP=∠APC，∵AB与⊙O相切于点B，∴OB⊥AB，∴∠ABO=90°，∴∠ABP+∠OBP=90°，∵OA⊥AC，∴∠OAC=90°，∴∠ACB+∠APC=90°，∴∠ABP=∠ACB，∴AB=AC；（2）设⊙O的半径为r，在Rt△AOB中，AB2=OA2﹣OB2=52﹣r2，在Rt△ACP中，AC2=PC2﹣PA2，AC2=（2）2﹣（5﹣r）2，∵AB=AC，∴52﹣r2=（2）2﹣（5﹣r）2，解得：r=1，则⊙O的半径为1．【点睛】本题考查了圆的切线的性质，圆的切线垂直于经过切点的半径；并利用勾股定理列等式，求圆的半径；此类题的一般做法是：若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系；简记作：见切点，连半径，见垂直．20、(1)见解析;(1)【解析】试题分析：先用列表法写出点Q的所有可能坐标，再根据概率公式求解即可.（1）由题意得

1

1

-1

（1，-1）

（1，-1）

-1

（1，-1）

（1，-1）

-2

（1，-2）

（1，-2）

（1）共有6种等可能情况，符合条件的有1种P（点Q在直线y=−x−1上）=.考点：概率公式点评：解题的关键是熟练掌握概率公式：概率=所求情况数与总情况数的比值.21、（1）y＝－(x－3)2＋5（2）5【解析】

（1）设顶点式y=a（x-3）2+5，然后把A点坐标代入求出a即可得到抛物线的解析式；

（2）利用抛物线的对称性得到B（5，3），再确定出C点坐标，然后根据三角形面积公式求解．【详解】(1)设此抛物线的表达式为y＝a(x－3)2＋5，将点A(1，3)的坐标代入上式，得3＝a(1－3)2＋5，解得∴此抛物线的表达式为(2)∵A(1，3)，抛物线的对称轴为直线x＝3，∴B(5，3)．令x＝0，则∴△ABC的面积【点睛】考查待定系数法求二次函数解析式，二次函数的性质，二次函数图象上点的坐标特征，掌握待定系数法求二次函数的解析式是解题的关键.22、今年妹妹6岁，哥哥10岁．【解析】

试题分析：设今年妹妹的年龄为x岁，哥哥的年龄为y岁，根据两个孩子的对话，即可得出关于x、y的二元一次方程组，解之即可得出结论．试题解析：设今年妹妹的年龄为x岁，哥哥的年龄为y岁，根据题意得：解得：．答：今年妹妹6岁，哥哥10岁．考点：二元一次方程组的应用．23、（1）商场至少购进乙种电冰箱14台；（2）商场购进甲种电冰箱28台，购进乙种电冰箱14（台），购进丙种电冰箱38台．【解析】

（1）设商场购进乙种电冰箱x台，则购进甲种电冰箱2x台，丙种电冰箱（80-3x）台，根据“商场最多支出132000元用于购买这批电冰箱”列出不等式，解之即可得；（2）根据“总利润=甲种冰箱利润+乙种冰箱利润+丙种冰箱利润”列出W关于x的函数解析式，结合x的取值范围，利用一次函数的性质求解可得．【详解】（1）设商场购进乙种电冰箱x台，则购进甲种电冰箱2x台，丙种电冰箱（80﹣3x）台．根据题意得：1200×2x+1600x+2000（80﹣3x）≤132000，解得：x≥14，∴商场至少购进乙种电冰箱14台；（2）由题意得：2x≤80﹣3x且x≥14，∴14≤x≤16，∵W=220×2x+260x+280（80﹣3x）=﹣140x+22400，∴W随x的增大而减小，∴当x=14时，W取最大值，且W最大=﹣140×14+22400=20440，此时，商场购进甲种电冰箱28台，购进乙种电冰箱14（台），购进丙种电冰箱38台．【点睛】本题主要考查一次函数