4.9数组常用算法-专题辅导课件

C程序设计专题辅导课

算法基础

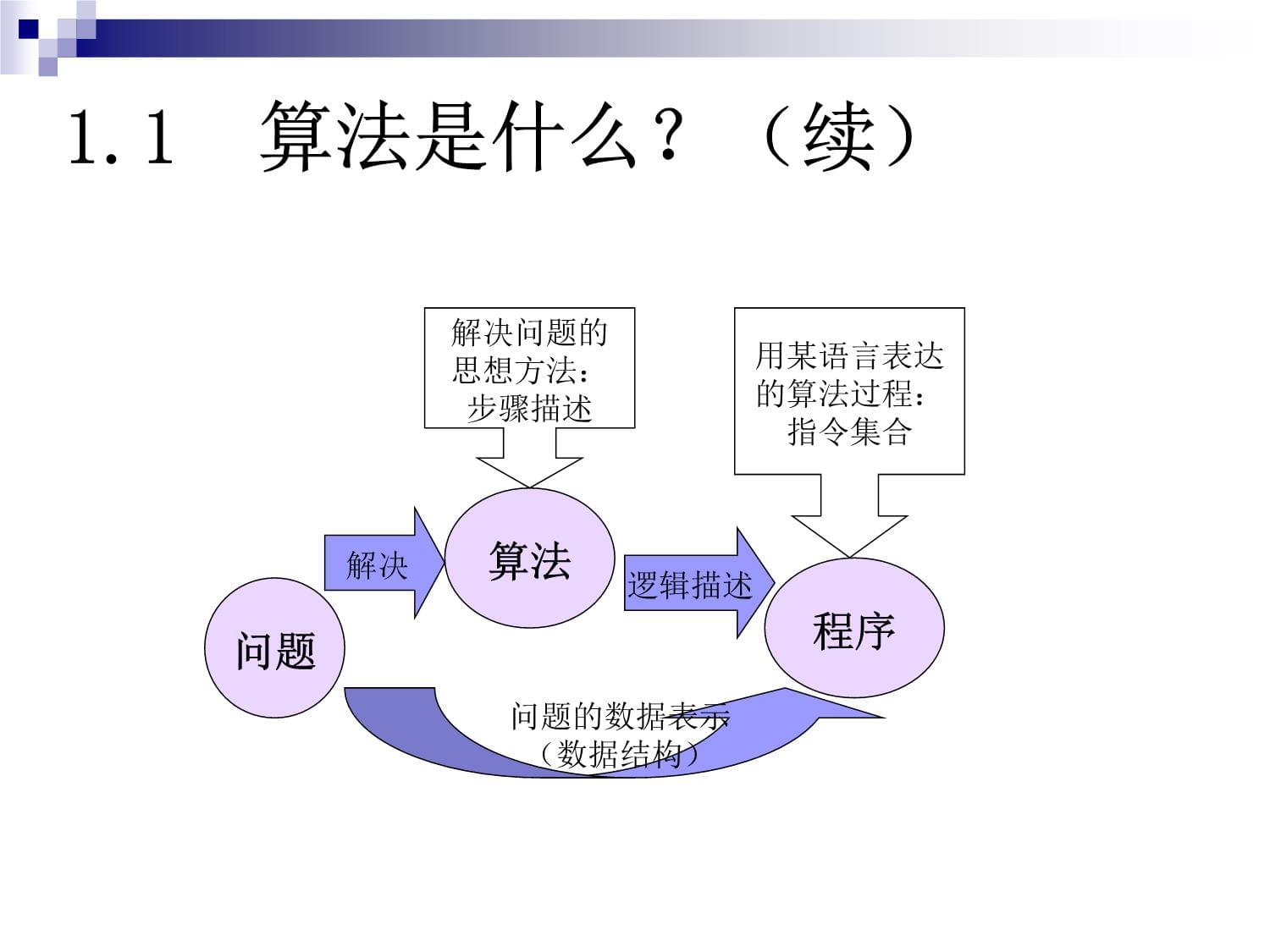
内容提要：算法(algorithm)的概念算法的表达典型算法及其实现—排序查找其它算法一、算法的概念1.1算法是什么？1.2算法的五个要素1.3简单算法－程序的例子1.1算法是什么？算法：解决特定类型问题的方法和步骤著名的Wirth公式：数据结构+算法=程序1.1算法是什么？（续）算法程序逻辑描述解决问题的思想方法：步骤描述用某语言表达的算法过程：指令集合问题解决问题的数据表示（数据结构）1.2算法的五个要素确定性：对同一个算法，相同的输入应该得到相同的输出，不会因为不同的机器和不同时间运行而不同有穷性：算法中的步骤应该是有限的，否则计算机就会永远无休止地执行程序有效性：算法中的每一个步骤都应该能被有效地执行，并应能得到一个明确的结果（大象装入冰箱的问题）输入：有零个或多个输出：有一个或多个

1.3简单算法－程序的例子欧几里德（Euclid）算法：求两个正整数A和B的最大公约数计算过程举例：设A=18B=30①A=30B=18②C=A%B=12③A=18B=12④C=A%B=6⑤A=12B=6⑥C=A%B=0⑦最大公约数就是B=6第一步：比较A和B这两个数：A设置为较大的数，B为较小的数；第二步：A除以B，得到余数C；第三步：如果C等于0，则最大公约数就是B，算法结束；否则将B赋值给A，C赋值给B；第四步：重复进行第二步、第三步。int

Euclid(inta,intb){intc;

if(a<b){c=a;a=b;b=c;}

while(c=a%b){a=b;b=c;}returnb;}二、算法的表达2.1用自然语言描述算法2.2用流程图描述算法2.3用伪代码描述算法2.1用自然语言描述算法问题：判断一个正整数n是否为素数的算法。算法描述一：将n作为被除数，用2到n平方根的各个整数轮流去除，如果都不能整除，则n是素数；否则n不是素数。算法描述二：第一步：输入n的值,计算n的平方根m；第二步：j=2(用j去除n)；第三步：n被j除，得到余数a；第四步：如果a==0，表示n能被j整除，

显示信息“n不是素数”，算法结束；

否则进入下一步；第五步：将j加1送回给j；第六步：如果j<=m,则跳到第三步执行；

否则显示“n是素数”的信息，算法结束。2.2用流程图描述算法2.3用伪代码描述算法int

prime(intn){m=n的开方;for(j=2;j<=m;j++){if(n被j整除)

break;}if(j>m)return1;/*是素数*/elsereturn0;

/*不是素数*/}欧几里德（Euclid）算法：int

Euclid(inta,intb){if(a<b

)交换a和b;c=

a除以b的余数;while(c!=0){a=b;b=c;c=

a除以b的余数;}

returnb;

/*最大公因子*/}三、典型算法及其实现3.1排序算法

3.2查找算法

3.3常用算法举例

3.1排序算法1、选择排序2、冒泡排序3、插入排序4、*归并排序问题：给定n个元素的数组a，对其中的元素从小到大排序，结果仍然在数组a中。排序算法－选择排序35281设n=5；5个数是：35281(1)15283(2)2583(3)385(4)58排序算法－冒泡排序35281设n=5；5个数是：35281(1)3

2

5

1

8

(2)2

3

1

5

8

(3)2

1358

(4)1

2

358冒泡排序(伪代码算法)voidBubbleSort(inta[],intn){

for(end=n-1;end>0;end--){

for(i=0;i<end;i++)if(

a[i]>a[i+1]){交换a[i]和a[i+1];}}

}

Entern:5Enter10integers:35281Aftersorted:12358排序算法－插入排序void

InsertionSort(inta[],intN){

intj,P;

int

Tmp;

for(P=1;P<N;P++){

Tmp=a[P];/*下一个元素*/

for(j=P;j>0&&a[j-1]>Tmp;j--) a[j]=a[j-1]; /*前面已排序的部分元素后移，在合适地方的给新元素留出位置*/ a[j]=Tmp;/*新来元素放入合适的位置*/}/*for-P循环结束*/}排序算法－插入排序35281设n=5；5个数是：35281(1)3(2)3

5(3)23

5(4)23

5

8(5)123

5

8

1、合并两个有序序列：1132426215273812AptrBptrCptrAptrCptrBptrCptr排序算法－归并排序void

MSort(intA[],int

TmpArray[],intLeft,intRight){

intCenter;

if(Left<Right){/*还有元素需要排序*/ Center=(Left+Right)/2;

MSort(A,TmpArray,Left,Center);

MSort(A,TmpArray,Center+1,Right);

Merge(A,TmpArray,Left,Center+1,Right);}}void

Mergesort(intA[],intN){

int

TmpArray[MAXSIZE];/*临时工作空间*/

MSort(A,TmpArray,0,N-1);

}2、递归归并排序算法/*Lpos=左半边起始位置,Rpos=右半边起始位置*/void

Merge(intA[],int

TmpArray[],int

Lpos,int

Rpos,int

RightEnd){

inti,LeftEnd,NumElements,TmpPos;

LeftEnd=Rpos-1;

TmpPos=Lpos;

NumElements=RightEnd-Lpos+1;

while(Lpos<=LeftEnd&&Rpos<=RightEnd)/*mainloop*/

if(A[Lpos]<=A[Rpos])

TmpArray[TmpPos++]=A[Lpos++];

else

TmpArray[TmpPos++]=A[Rpos++];

while(Lpos<=LeftEnd)/*Copyrestoffirsthalf*/

TmpArray[TmpPos++]=A[Lpos++];

while(Rpos<=RightEnd)/*Copyrestofsecondhalf*/

TmpArray[TmpPos++]=A[Rpos++];

for(i=0;i<NumElements;i++,RightEnd--)

/*CopyTmpArrayback*/

A[RightEnd]=TmpArray[RightEnd];}3、迭代（非递归）归并排序算法A0123…………n4n3n2n1…………………………排序算法－归并排序设n=6；6个整数是：352871(1)352871(2)3

5

28

17

(3)23

58

17

(4)123

5

78

352817(1)352

871(2)3

5

2

87

1

(3)3

5

2

8

7

1(3’)3

5

2

78

1(2’)23

5

178(1’)123

5

78

迭代算法示例：递归算法示例：3.2查找算法1、顺序查找2、二分查找3、二分查找推广－非线性方程的根问题：给定n个元素的数组a，查找某元素x是否在数组a中。如果在，返回该元素在数组中的下标，否则返回-1。顺序查找——从列表的第一个数据（或叫做元素）开始，如果给定的数据和表中的数据匹配时，查找过程结束，给出这个数据所在表中的位置（下标）。3.2查找算法－顺序查找int

Find(inta[],intn,intx){inti;/*n个元素存放在a[1]-a[n]中*/a[0]=x;/*“哨兵”*/

for(i=n;a[i]!=x;--i);returni;}int

Find(inta[],intn,intx){inti;

/*n个元素存放在a[0]-a[n-1]中*/

for(i=0;a[i]!=x&&i<n;++i);returni;}二分查找——也叫折半查找。比较列表处于一半（中间）位置的数据是否与要查找的数x相同，相同则结束查找，否则判断是在前半部分还是后半部分（根据列表的排序确定的），然后继续同样的查找过程。

查找不成功的条件是查找区间已经<=0。3.2查找算法－二分查找二分查找要求数据已经排序。二分查找比顺序查找快得多！3.2二分查找算法一个有点类似的问题－－猜价格游戏：保证在较短时间内猜出一件商品的价格（假设给定价格区间[10,1000]元,且是整数）。条件：当报出一个价格时，系统提示：高了、低了或正确。3.2二分查找算法二分查找算法（自然语言描述）：假设数组A的当前查找区间的下标为[low,high]，查找元素为x；

(1)若high<low，查找失败，算法结束；否则取区间中间下标：mid=(low+high)/2;(2)若x<A[mid]，x在[low,high]的左半区，则调整新区间边界：low不变,high=mid-1，转(1)；(3)若x>A[mid]，x在[low,high]的右半区，则调整新区间边界：low=mid+1,high不变，转(1)；(4)若x==A[mid]，则找到，算法结束。int

BiSearch(intx,intA[],intn){/*n个元素存放在A[1]—A[n]*/

int

low,high,mid；low=1;high=n;while(low<=high){mid=(low+high)/2;if(x<A[mid])high=mid-1;/*x在左半区*/elseif(x>A[mid])low=mid+1;/*x在右半区*/elsebreak;/*找到！*/}if(low<=high)returnmid;elsereturn0;}

3.2二分查找程序3.2二分查找推广－非线性方程求根设有非线性方程：

f(x)=0其中f(x)在[a,b]区间内连续且f(a)f(b)<0。因而f(x)在[a,b]区间内至少有一个实根x0，即：f(x0)=0。写一个程序求f(x)在[a,b]区间内的一个近似实根。结束条件：|f(x)|<ε

或b-a<ε二分法求非线性方程的根二分法求根（自然语言描述）：假设f(x)在[a,b]内连续，且f(a)f(b)<0，给定误差ε；

(1)若b-a<ε,返回x0=(a+b)/2作为近似根，算法结束；否则取区间中点m=(a+b)/2;若f(m)=0,返回x0=m,算法结束；(2)若f(a)f(m)>0，在[m,b]内必有根，则调整新区间边界：b不变,a=m，转(1)；(3)若f(a)f(m)<0，在[a,m]内必有根，则调整新区间边界：a不变,b=m，转(1)；double

BiRoot(doublex,double

a,doubleb,doubleeps){/*求值函数doublef(doublex)需要另外定义*/ doublemid,fm,fa=f(a),fb=f(b);

if(fa==0.)returna;if(fb==0.)returnb;

if(fa*fb>0.){FatalError(“Fail”);return0.;}while(b-a>eps){mid=(b+a)/2;fm=f(mid);if(fm)==0.)returnmid;/*找到一个根*/elseif(fm*fa>0.){a=m;fa=fm;}/*留右半区*/else{b=m;fb=fm;}/*留左半区*/}}

3.2二分法求根3.3常用算法举例例1：输入n（2≤n≤5，程序不需要对此范围进行判断），再输入n个整数保存到数组a中，通过循环查找n个数中是否有重复的数，如果有则输出Yes，否则输出No。

要求在循环过程中，任何两个数的比较次数不得超过1次（比如对a[0]与a[1]比较后接下去又对a[1]与a[0]比较是不符合要求的），并且要求一旦找到有数重复则立即结束循环。

－－

08年夏考题

#include<stdio.h> voidmain() {inta[5],i,j,n;

scanf("%d",&n);

for(i=0;i<n;i++)

scanf("%d",&a[i]);

for(i=0;i<=n-2;i++){ for((1);j<=n-1;j++){

if(a[i]==a[j])(2); } if((3))

break; } if((4))

puts("No"); else

puts("Yes");

}j=i+1breakj<=n-1i==n-1或i>=n-1或i>n-23.3常用算法举例例2：函数f(A,…,x)有三个参数,它们分别是已排序(升序)的数组A、整数n(A的当前元素个数)以及x(要插入到A中的整数)。函数f(…)的功能是把x插入A中，而A仍然保持升序，但n增加了1。例如,A的原来5个元素是(2,4,6,8,10),n=5,x=1,程序运行结束后的输出是1#2#4#6#8#10#。请完成下面程序。

－－06年考题

#include<stdio.h>voidfintA[],int*n,intx){inti;i=__(1)__;while((i>0)&&(x<A[i-1])){__(2)__; i--;}

A[i]=x;(*n)++;}voidmain(){

inti,A[10]={2,4,6,8,10},n=5,x=1;f(______(3)_______);

for(i=0;i<n;i++)

printf("%d#",A[i]);}*nA[i]=A[i-1];A,&n,x3.3常用算法举例例3：数组元素循环后移问题一个数组中存有n（1<=n<=100）个整数，在不允许使用另外数组的前提下，将每个数顺序向后移m（m>=0）个位置（最后m个数循环移至最前面的m个数）。输入n、m及n个整数，输出循环后移m位以后的n个整数。输入：62123456输出：561234

数组元素循环后移问题（续）1．问题分析输入的n个整数可以放在一个一维数组中，循环右移一位的操作重复进行m次即可。这种做法的数据移动次数大约是m(n+1)次。2．要点A）“循环右移一位的操作重复进行m次”，B）m可以处理成小于n的数，以减少工作量。当m>n时，可以用m%n代替m，效果相同。但移动次数大约是(m%n)*(n+1)次。

#include<stdio.h>voidshift(intarray[],intn){

inti,array_end;

array_end=array[n-1];

for(i=n-1;i>0;i--)/*n个元素循环位移1位*/

array[i]=array[i-1];

array[0]=array_end;}voidmain(){intnumber[100],n,m,i;……/*输入*/m%=n;/*当m大于等于n时转化成等价的小于n的数*/for(i=0;i<m;i++)

shift(number,n);/*n个元素循环位移1位*/……

/*输出*/}数组元素循环后移问题（续）思考1：如果修改题目要求，允许使用另外一个大小为m（假设n>m>0）数组，则如何提高程序效率？

012345234501思考2：不改变题目的任何限定(即不允许使用另外数组)，能否设计一种移动次数不超过(n+gc)的方法？[gc是最大公约数]

例：n=6,m=4gc=2趟每趟移动n/gc=3个数0tmp:240voidshift_m(intarray[

],intn,intm){

inti,tmp[M];

/*M是>=m的常数*/

for(i=n-1;i>=n-m;i--)/*复制保留最后m个元素*/

tmp[i-n+m