初中九年级数学课件-28.2.1 解直角三角形_第1页
初中九年级数学课件-28.2.1 解直角三角形_第2页
初中九年级数学课件-28.2.1 解直角三角形_第3页
初中九年级数学课件-28.2.1 解直角三角形_第4页
初中九年级数学课件-28.2.1 解直角三角形_第5页
已阅读5页，还剩5页未读， 继续免费阅读

下载本文档

版权说明：本文档由用户提供并上传，收益归属内容提供方，若内容存在侵权，请进行举报或认领

文档简介

28.2.1解直角三角形

参赛教师张鑫时间：2020年8月27日九年级-上册-第二十八章锐角三角函数你认为货船继续向西航行途中会有触礁的危险吗?B

想一想船有无触礁的危险吗？1、审题，画图。

茫茫大海中有一个小岛A,该岛四周16海里内有暗礁.今有货船由东向西航行,开始在距A岛30海里南偏东600的B处,货船继续向西航行。60º观测点被观测点A北C30海里？这个问题归结为:在Rt△ABC中,已知∠A=60°,斜边AB=30,求AC的长（2）航线BC和⊙A相切，会触礁暗礁圆形区和航线的位置关系（用圆心A到航线的距离AC与暗礁区半径r=16的关系来区分)。

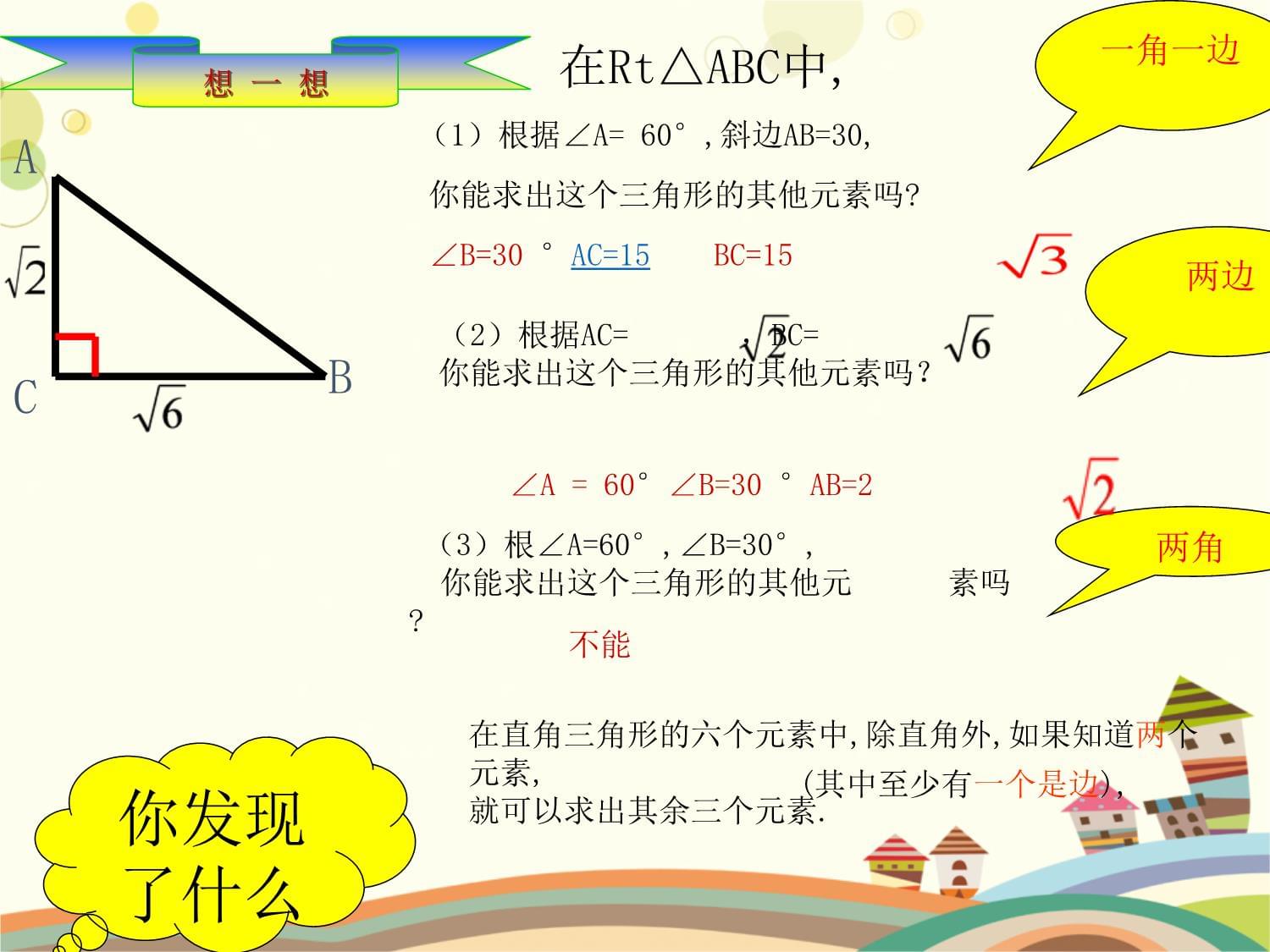
（1）航线BC和⊙A相离,不会触礁（3）航线BC和⊙A相交，会触礁AC>16AC=16AC<16Ar=16BAr=16BAr=16BCCC分析在Rt△ABC中,（1）根据∠A=60°,斜边AB=30,A在直角三角形的六个元素中,除直角外,如果知道两个元素,就可以求出其余三个元素.(其中至少有一个是边),想一想你发现了什么BC∠B=30°AC=15BC=15∠A=60°∠B=30°AB=2一角一边两边（2）根据AC=，BC=你能求出这个三角形的其他元素吗？两角

（3）根∠A=60°,∠B=30°,

你能求出这个三角形的其他元素吗?不能你能求出这个三角形的其他元素吗?在直角三角形中,由已知元素求未知元素的过程,叫解直角三角形(1)三边之间的关系:a2＋b2＝c2（勾股定理）；解直角三角形的依据(2)锐角之间的关系:∠A＋∠

B＝90º；(3)边角之间的关系:AＣBabctanA＝absinA＝accosA＝bcsinB＝bccosB＝actanB＝ab

如图，Rt△ABC中，∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c，则有：┌例:在Rt△ABC中,∠C=90°,∠B=35°,b=20,解这个直角三角形.(精确到0.1)ＡＣＢabc参考值tan35°≈0.70sin35°≈0.57cos35°≈0.82试一试解:∵尽量选择原始数据,避免累积错误35°20？？？∵sinB=b/c∴c=b/sinB=20/sin35°≈34.9∵∴┌即：取原避中(1)∠B＝72°，c=14.ABCbac=14解：∵∵∴∴∴b=csinB=14xsin72°≈13.3a=ccosB=14xcos72°≈4.34

有斜用弦，

有斜用弦，

在Rt△ABC中，∠C＝90°，根据下列条件解直角三角形：（数值保留根号或保留三位有效数字，角度精确到0.1°）练习考一考

在Rt△ABC中，∠C＝90°，根据下列条件解直角三角形：（数值保留根号或保留三位有效数字，角度精确到0.1°）（2）a=30,b=20;解：根据勾股定理ABCb=20a=30c∵∴∴

无斜用切，考一考小结在遇到解直角三形的问题时，最好先画一个直角三角形的草图，按题意标明哪些元素是已知的，哪些元素是未知的，以

利于分析解决问题;选取关系式时要尽量利用原始数据，即”取原避中”,以防止“累积错误”;

人人文库> 全部分类> 教育资料 > 课件下载

温馨提示

  • 1. 本站所有资源如无特殊说明，都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
  • 2. 本站的文档不包含任何第三方提供的附件图纸等，如果需要附件，请联系上传者。文件的所有权益归上传用户所有。
  • 3. 本站RAR压缩包中若带图纸，网页内容里面会有图纸预览，若没有图纸预览就没有图纸。
  • 4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
  • 5. 人人文库网仅提供信息存储空间，仅对用户上传内容的表现方式做保护处理，对用户上传分享的文档内容本身不做任何修改或编辑，并不能对任何下载内容负责。
  • 6. 下载文件中如有侵权或不适当内容，请与我们联系，我们立即纠正。
  • 7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

最新文档

评论

0/150

提交评论