沪教版数学八年级下册填空题解答题专项训练100题含答案

沪教版数学八年级下册填空题解答题专项训练100题含答案

一、填空题

1.如图，正方形ABCO中，对角线AC,8。交于点O,E点在BC上，EGLOB,

EFVOC,垂足分别为点G,F,AC=10,则EG+EF=.

GZXF

BEC

2.如图，菱形ABCD的周长为4石，对角线AC和BD相交于点O,

AC：BD=1：2,贝IAO：BO=,菱形ABCD的面积S=.

3.如图，点E在正方形ABCD的边BA的延长线上，连接AC,AC=AE,CE交AD

于点F,则/ACE的度数等于.

EAB

4.一个不透明的口袋中有红球和黑球共25个，这些球除颜色外都相同.进行大量的

摸球试验（每次摸出1个球）后，发现摸到黑球的频率在0.6附近摆动，据此可以估

计黑球为一个.

5.函数y=H+b（k,b都是常数，且〃力0）叫做,当b=0时，函数

y=kx（%是常数，kxO）叫做,常数/叫做.

6.如图，在矩形ABCD中，AC、BD交于点O,M、N分别是A8、04的中点.若

MN=2,CD=4,则NACB的度数为.

7.如图，口ABCD中，ZABC=60°,E、F分别在CD和BC的延长线上，AE〃BD,

EF1BC,EF=3,则AB的长是

8.如图，在△ABC中，D,E分别是48,AC的中点，尸是线段。E上一点，连接

9.在一个暗箱里放入除颜色外其它都相同的1个红球和11个黄球，搅拌均匀后随机

任取一球，取到红球的概率是.

10.在一个不透明的袋中装有12个红球和若干个黑球，每个球除颜色外都相同，任意

摸出一个球是黑球的概率为!，那么袋中的黑球有个.

11.四边形A8C。是边长为4的正方形，点E在边A。上，以EC为边作正方形CEFG

(点D,点F在直线CE的同侧).连接BE(1)如图1,当点£与点4重合时，BF=

；(2)如图2,当点E在线段AD上时，AE=\,贝UBF=.

12.小明在一次用“频率估计概率”的试验中，把“定西的黄土地黄而厚实''中的每个汉

字分别写在同一种卡片上，然后把卡片无字的面朝上，随机抽取一张，并统计了某一

结果出现的频率，绘制了如图所示的折线统计图，则符合这一结果的试验最有可能抽

出的是字.

k3

13.若反比例函数y=的图象经过点（2,-j）,则一次函数

y="—左仕中0）的图象不经过第象限.

14.顺次连接矩形各边中点所得四边形为形.

15.若一个反比例函数的图象与直线y=2x-6的一个交点为2）,则这个反比

例函数的表达式是.

16.一次函数y=（k+l）x-2的函数值y随自变量x的增大而减小，那么％的取值范围

是.

17.若直线y=2x+b经过点（-1,3）,则b的值为.

18.盒子里有3张形状、大小、质地完全相同的卡片，上面分别标着数字0、1、2,

从中随机抽出1张后放回再随机抽出1张，则两次抽出的卡片上的数字都是奇数的概

率是.

19.如图，在ZkABC中，AB=4C=7,BC=5,AFIBC^F,BE_LAC于E,0是4B的

中点，则AOE尸的周长是.

20.如图，分别以MZiABC的斜边AB、直角边AC为边向外作等边△48。和AACE,

F为AB中点，连接OF、EF、DE.EF与AC交于点O,OE与交于点G,连接OG,

若NB4c=30,下列结论：①®AD=AEt③E/JLAC；④

AD=4AG.其中正确的结论的序号是.

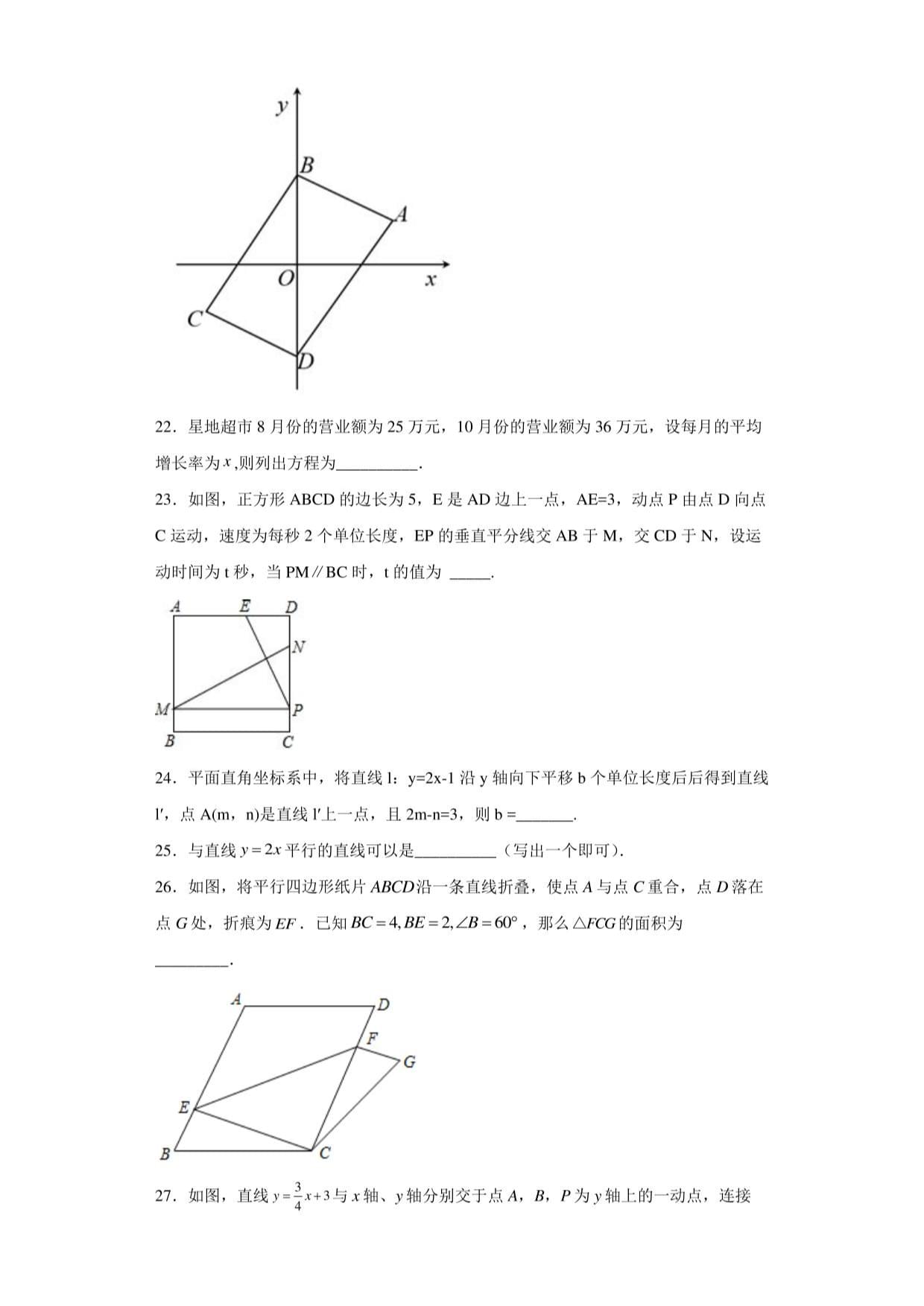
21.如图，平面直角坐标系中，点B,点。的坐标分别为（0,2）和（0,-2）,以

8。为对角线作团AB8,若点A的坐标为（2,1）,则点C的坐标为.

y

22.星地超市8月份的营业额为25万元，10月份的营业额为36万元，设每月的平均

增长率为x，则列出方程为.

23.如图，正方形ABCD的边长为5,E是AD边上一点，AE=3,动点P由点D向点

C运动，速度为每秒2个单位长度，EP的垂直平分线交AB于M,交CD于N,设运

动时间为t秒，当PM〃BC时，I的值为.

24.平面直角坐标系中，将直线1：y=2x-l沿y轴向下平移b个单位长度后后得到直线

1',点A(m,n)是直线1'上一点，且2m-n=3,贝!Ib=.

25.与直线y=2x平行的直线可以是(写出一个即可).

26.如图，将平行四边形纸片A8C。沿一条直线折叠，使点A与点C重合，点。落在

点G处，折痕为EF.已知BC=4,8E=2,48=60。，那么△尸CG的面积为

27.如图，直线y=：x+3与x轴、y轴分别交于点A,B,P为y轴上的一动点，连接

AP,若将-皿沿直线”翻折，使点8恰好落在x轴上的点8'处，则符合条件的点

28.如图“是长方形纸带，NDEF=26,将纸带沿EF折叠成图b,再沿8尸折叠成图

c,则图。中的NCFE的度数是度.

29.如图，直线y=x-3分别交x轴、y轴于B、4两点，点C(0,1)在y轴上，点

P在x轴上运动，则/PC+PB的最小值为一.

30.如图，在边长为2cm的正方形ABCD中，点Q为BC边的中点，点P为对角线

AC上一动点，连接PB、PQ,则P8Q周长的最小值为—cm(结果不取近似值).

31.直线y=-2x+A与两坐标轴围成的三角形的面积为4,则b的值为.

32.已知电路AB由如图所示的开关控制，闭合a,b,c,d,e五个开关中的任意两个，则

使电路形成通路的概率是.

33.如图，已知直线y=-x+3与直线y=x交于点H,与反比例函数y（A>0）

X

的图象在第一象限交于点A,B,与两坐标轴交于点C,D.

（1）当点A的坐标为（2,1）时，k的值为

（2）在（1）的条件下，线段"A的长为

34.若关于x的分式方程空4=1的解为正数，则。的取值范围为.

x-l

35.皮皮玩走如图所示的迷宫游戏.他每遇到一扇门就从里走出，然后随机左转或右

转继续前行，规定走进死胡同则算失败.那么皮皮从迷宫中心O成功走出这个迷宫的

37.如下图，将边长为9cm的正方形纸片ABCD折叠，使得点A落在边CD上的

E点，折痕为MN.若CE的长为6cm,则MN的长为cm.

M

38.已知多边形的每个内角都等于135。，求这个多边形的边数是.(用两种方法

解决问题)

39.正方形ABG。、4鸟GG、A3B,C3C2……按如图的方式放置，点A，4,A,…

和点C-C2IG…分别在直线，="+/%>0)和x轴上，已知点片(1,1),8式3,2),

按此规律，则点鸟的坐标是

40.平面直角坐标系中，点P(x,y)的横坐标X的绝对值表示为|x|,纵坐标y的绝对值

表示为lyl,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股

值，记为[P],即[P]=|x|+lyl(其中"+”是四则运算中的加法).

(1)已知点4T3),8(石+2,V3-2),则勾股值网+网的值为

(2)满足条件W]=3的所有点N围成的图形的面积是

41.矩形是的平行四边形.因此它具有平行四边形的一切性质，此

外矩形还具有的性质是四个角和对角线.

x>a

42.已知方程=-a=J—,且关于x的不等式组只有4个整数解，那么b的

a-44-a,

x<b

取值范围是.

43.某网店老板经营销售甲、乙两种款式的浮潜装备，每件甲种款式的利润率为

30%,每件乙种款式的利润率为50%,当售出的乙种款式的件数比甲种款式的件数少

40%时，这个老板得到的总利润率是40%；当售出的乙种款式的件数比甲种种款式的

件数多80%时，这个老板得到的总利润率是.

44.已知直线，="+占与x轴的交点在A（3,0）和8（4,0）之间，（包括A、8两点），直

^y=kx+b-3k^x轴交于点（机0），则m的取值范围.

45.在-2,1,乃，-3,0这5个数中，任取一个数是负数的概率是.

46.如图，折叠矩形纸片ABC。，使点B落在点。处，折痕为MV,已知

AB=8,AD-4,求MN的长是.

47.已知函数，=履+6的图像过点（0,-1）和（-1,1）,且点（a，X）和点Q+1,%）都在

这个函数图象上，则匕与外的大小关系是

二、解答题

48.解分式方程:ZZZ__L

y-3=23-y

49.28AC为钝角，S_LAB,BEYAC,垂足分别为。、E,M是BC中点，求证:

ME=MD.

50.如图，在平行四边形A8C。中，点E,尸分别在A£）,BC上，DE〃BF,若

ZBED=NDFB.

（1）求证：AE=CF.

（2）求证：四边形是平行四边形.

51.近年来，电商平台直播带货成了一个火热的新兴职业.某主播带货图书《苏东坡

传》，他用双语直播，风趣幽默，点燃了不同年龄者的读书热情.已知这本书的成本价

为10元，规定销售单价不低于成本价，且不高于成本价的3倍，通过前几天的销售发

现，该书每天的销售量y(本)与销售单价x(元/本)之间近似满足一次函数关系，部

分对应数据如下表：

X(元/本)1525

y(本)700500

(1)根据表格提供的数据，求y关于x的函数关系式，并写出x的取值范围.

(2)若销售该书每天的利润为6000元，求该书的销售单价.

(3)销售该书每天的利润能否达到9000元？请说明理由.

52.一枚质地均匀的正方体骰子，六个面上分别标有数字-3,-1,0,1,2,4这六个

数，若将第一次掷出的骰子正面朝上的数记为由，第二次掷出的骰子正面朝上的数记

为〃，则点尸记作(根,〃).请用画树状图或列表法求点尸(〃?,〃)恰好落在第二象限的概

率.

53.已知一次函数丫=依+左一1(其中人为常数且左/0)经过点(2,5).

(1)求一次函数的表达式；

(2)当机4x4帆+3时，记函数的最大值为M,最小值为N,求M-N的值.

54.如图，在YA8CD中，点E、尸分别在边C。、AB上，且AE=CF,连接EF,

请只用无刻度的直尺画出线段EF的中点O,并说明这样画的理由.

55.如图，在正方形ABCD中，点P是对角线8。上的一点，点E在AO的延长线

上，且％=PE,PE交CD于点F.

(1)证明：PC=PE；

(2)求NCPE的度数.

56.某市居民用水实行阶梯收费，每户每月用水量如果未超过20吨，按每吨3元收

费.如果超过20吨，未超过的部分按每吨3元收费，超过的部分按每吨4.5元收

费.设某户每月用水量为工吨，应收水费为了元.

（1）若每月用水量不超过20吨，则丁与x之间的关系式为.

（2）若该户四月份平均水费为每吨3.7元，则该户四月份的用水量为吨.

57.某市电力公司为了鼓励居民用电，采用分段计费的方法计算电费，每月用电不超

过100度，按每度0.48元计算，每月用电超过100度，其中的100度仍按原标准收

费，超过部分按每度0.50元计费.

（1）设月用电x度时，应交电费y元，写出y与x的函数关系式，并写出自变量的取

值范围.

（2）小王家一月份用电130度，应交电费多少元？

（3）小王家二月份交电费70元，求小王家二月份用了多少度电？

58.已知：如图，在正方形A8CO中，G是对角线8。上的一点，GEVCD,

GFLBC,E,尸分别为垂足，连结AG,EF,求证：AG=EF.

BFC

59.如图，已知在oABCD中，AB=4cm,AD=6cm,NABC的平分线交AD于点E,

交CD的延长线于点F,则DF=______cm.

60.如图，在平行四边形ABC。中，点E、尸分别在AB、边上，连接CE、AF,

NDCE=NBAF.

试判断四边形AECF的形状并加以证明.

E

61.如图1,直线4：y=-；x+3与X轴、y轴分别交于点A和点5,直线4：y=gx+6

与x轴、y轴分别交于点C和点O,与直线4相交于点E（4,〃?）.

（2）若点尸为线段BE上的一动点，连接尸0、PC,当APCO的面积为2时.求出点P

的坐标；

（3）如图2,在（2）的条件下，将直线6沿射线CP的方向平移，使其平移后的直线4

恰好经过点P,平移后点力的对应点为以，点例为y轴上一动点，点N为直线4上一

动点，请建军与出所有使得以点P、限M、N为顶点的四边形是平行四边形的点N

的坐标.

62.某小商品批发商批发的4、B两种商品的成本和批发价如表所示：

成本（元件）批发价（元/件）

A33.4

B3.54

该批发商花了32000元购进4,B两种商品若干件，立刻销售一空，共盈利4400元.

（1）该批发商分别购进A,B两种商品各多少件？

（2）由于畅销，该批发商决定再购进A,2两种商品共30000件，其中B商品的数量不

多于A商品数量的2倍，那么该批发商购进A、B两种商品各多少件时会获得最大利

润，最大利润是多少？

63.如图，在四边形ABCD中，AD〃BC,ZA=90°,AB=BC,ZD=45°,C£）的

垂直平分线交CO于E,交AO于尸，交的延长线于G,若AO=a.

C

BG

(1)求证：四边形ABB是正方形；

⑵求BG的长.

64.某校“六一”活动购买了一批A,8两种型号跳绳，其中A型号跳绳的单价比3型

号跳绳的单价少9元，己知该校用2600元购买A型号跳绳的条数与用3500元购买B

型号跳绳的条数相等.

(1)求该校购买的A,B两种型号跳绳的单价各是多少元？

(2)若两种跳绳共购买了200条，且购买的总费用不超过6300元，求A型号跳绳至

少购买多少条？

65.小明在学习完电学知识后，用四个开关A、B、C、D,一个电源和一个灯泡设计

了一个如图所示的电路图.

(1)在开关A闭合的情况下，任意闭合8、C、。中的一个开关，则灯泡发光的概率等

于:

(2)任意闭合其中两个开关，请用树状图或列表的方法求出灯泡发光的概率.

66.如图，平面直角坐标系中点40,3)和点B(4,0),点为坐标平面内一动点,

且为等腰三角形，求点M的坐标.

67.某商场计划购进A,8两种型号的手机，已知每部A型号手机的进价比每部8型

号手机进价多500元，每部A型号手机的售价是2500元，每部B型号手机的售价是

2100元.

（1）若商场用50000元共购进A型号手机10部，B型号手机20部，求A、8两种型

号的手机每部进价各是多少元？

（2）为了满足市场需求，商场决定用不超过7.5万元采购A、B两种型号的手机共40

部，且A型号手机的数量不少于B型号手机数量的2倍.

①该商场有哪几种进货方式？

②该商场选择哪种进货方式，获得的利润最大？

68.已知反比例函数y=：和一次函数），2=如+〃相交于点A（2,3）,B（-3,a）.

（1）求一次函数和反比例函数解析式；

（2）直接写出乂<%时x的取值范围.

69.荔枝是广西盛产的一种水果，六月份是荔枝传统销售旺季•去年六月份某水果公司

为拓展销售渠道，在实体店的基础上中途增设了网店，公司总销售量y（吨）与销售时

间双天）关系如图所示：

（1）请直接写出去年六月份网店每天的销售量，并求出AB的解析式（不写取值范围）；

（2）公司预计，今年六月份实体店的销售量与去年相同，网店的销售量将有所增加，预

计今年网店每天的销售量比去年增加加%,公司六月份的总销售量是去年的1.4倍，求

70.（1）已知关于x的方程也?=3的解是正数，求，”的取值范围

x-2

（2）若方程生?=3无解，求小的值.

x-2

71.如图①，在RtABC中，NAC3=90。，ZA=60°,CQ是斜边A8上的中线，点E

为射线8C上一点，将沿DE折叠，点B的对应点为点F.

图①

(1)若AB=a.直接写出CO的长(用含。的代数式表示);

(2)若。尸，8C,垂足为G,点F与点。在直线CE的异侧，连接CF,如图②,

判断四边形AOFC的形状，并说明理由;

(3)若。尸_LA8,直接写出N80E的度数.

72.解方程

x313

(1)------1=7・(2)-=-------.

x-1(x-l)(x+2)x2x+l

73.如图，在矩形ABC£>中，AD>AB,

(1)在54的延长线上求作点E,使DE=BE(尺规作图，保留作图痕迹，不写作法).

⑵在(1)的条件下，若Z)E〃AC,求NACB的度数.

74.如图，在1：43C中，CF1AB于F,BE_LAC于E,M为BC的中点，

BC=10.

(1)若ZABC=50。，ZACB=60°,求NEA"的度数；

(2)若EF=4,求MEF的面积.

75.如图，四边形ABCD是菱形，对角线AC和BD相交于点O,AC=8cm,

BD=6cm,DH_LAB于H.

(1)求菱形ABCD的面积；

(2)求DH的长.

76.（1）如图，已知AC、8c分别是—84。、NABE的平分线，且

Zl+Z2=ZACB.求证：AD//BE.

（2）一个质地均匀的骰子每个面上分别刻有1、2、3、4、5、6点，任意掷出骰子后

①求掷出的点数不大于4的概率；

②求掷出的点数能被3整除的概率.

77.小李家住房户型呈长方形，平面图如下（单位：米）.现准备铺设整个长方形地

面，其中三间卧室铺设木地板，其它区域铺设地砖（房间内隔墙宽度忽略不计）.

（1）求。的值；

（2）请用含x的代数式分别表示铺设地面需要木地板和地砖各多少平方米；

（3）按市场价格，木地板单价为300元/平方米，地砖单价为100元/平方米，已知卧

室2的面积为21平方米，求铺设地面的总费用.（木地板与地砖的总价和）

r«-2x-!-►+<-x-2x—

厨房卫生间

卧室2

卧室1

餐厅

客厅

卧室3

10J6------

78.你知道什么是“低碳生活”吗？“低碳生活”是指人们生活中尽量减少所耗能量，从

而降低碳（特别是二氧化碳）的排放量的一种生活方式.

排碳计算公式

家居用电的二靴碳排放量（kg）

;耗电量（kW・h）x0.785

开私家车的二氧化碳排放量（kg）

:耗潮1（L）x2.7

家用天然气二氧化碳排放量（kg）

=天然气使用量面）x0.19

家用自来水二氧化碳徘放量（kg）

=自来水使用量⑴x0.91

（1）如果用X（L）表示耗油量，用y（kg）表示开私家车的二氧化碳排放量，则y与

x之间的关系式可表示为；

（2）在上述关系式中，耗油量每增加1L,二氧化碳排放量增加kg.当耗油

量从1OL增加到1OOL时，二氧化碳排放量从kg增加到kg：

（3）小颖家本月家居用电的耗电量约为90kw.h、开私家车的耗油量约为70L、天然气

使用量约20m3、自来水使用量约6吨，请你计算一下小颖家本月这几项的二氧化碳排

放总量：

（4）你打算从哪些小事做起践行低碳生活？请直接写出两条.

79.列方程解应用题

某车间36名工人生产螺钉和螺母，每人每天平均生产螺钉500个或螺母800个，一个

螺钉要配两个螺母，为了使每天的产品刚好配套，应该分配多少名工人生产螺钉，多

少人生产螺母？

80.如图，一次函数），=辰+方的图象分别与x轴、V轴相交于点E和点尸，点E的坐标

为（-8,0）,点F的坐标为（0,6）,点A的坐标为（0,4）.点尸为直线E尸上的一个动点.

(1)求直线EF的解析式；

(2)若点P在点E、尸之间运动(不包含E、尸点)，求AO/%的面积S与x的函数关

系式，并写出自变量x的取值范围；

(3)探究：若点尸在直线E尸上运动，当点尸运动到什么位置时，AOR4的面积为

12?

81.甲加工A型零件60个所用时间和乙加工B型零件80个所用时间相同，每天甲、

乙两人共加工35个零件，设甲每天加工x个.

(1)直接写出乙每天加工的零件个数(用含x的代数式表示)；

(2)求甲、乙每天各加工多少个零件；

82.如图，矩形A3CD中，AB=4,AD=S,E在上，DE=3,点尸从点B出

发，以每秒1个单位长度的速度沿着8c边向终点C运动，连接尸E,设点P运动的时

间为f秒.

(1)过户作抨垂足为尸，用含，的式子表示：EF=,PC=；

(2)当r=2时，判断PEC是否是直角三角形，并说明理由；

(3)当NPEC=NDEC时,求f的值.

83.漆湖湿地风景区特色旅游项目：水上游艇.旅游人员消费后风景区可盈利10元/

人，每天消费人员为500人.为增加盈利，准备提高票价，经调查发现，在其他条件

不变的情况下，票价每涨1元，消费人员就减少20人.

(1)现该项目要保证每天盈利6000元，同时又要旅游者得到实惠，那么票价应涨价

多少元？

(2)若单纯从经济角度看，票价涨价多少元，能使该项目获利最多？

84.已知：如图，在DA8C£＞中，点扭、N分别是A3、CD的中点.求证：DM=BN.

85.如图，ABC中，ZACB=90°,。为4B中点，四边形BCE。为平行四边形,

DE、4c相交于点F.求证：

（1）点尸为AC的中点；

（2）试确定四边形AOCE的形状，并说明理由；

（3）若四边形AOCE为正方形，A8C应添加什么条件？并证明你的结论.

86.如图所示，可以自由转动的转盘被3等分，指针落在每个扇形内的机会均等.小

明和小华利用这个转盘做游戏，若采用下列游戏规则，你认为对双方公平吗？请用列

表或画树状图的方法说明理由.

87.综合与实践.

勤奋小组上网查询了本市滴滴快车和出租车计价规则，得到了如下信息:

滴滴打车收费标准：出租车收费标准：

起步价8元，即2公里以内只收取8元；

起步价8元，即3公里以内只收取8元；

超出2公里后，开始收取里程费和时长

超出3公里后，开始收取里程费，不收取

费，超出部分每公里收取里程费1.6元，

时长费，超出部分每分钟里程费2.4

超出部分每分钟收取时长费0.2元；（不足

元.（不足1公里按1公里计算）

1公里按1公里计算）

假定滴滴打车和出租车平均速度均为30公里/时，请按要求完成以下任务.

（1）根据勤奋小组的分析直接写出滴滴打车收费/（元）与里程x（公里）之间的函

数关系式和出租车收费内（元）与里程x（公里）之间的函数关系式；

（2）若小明准备打车去距离出发地。公里（0<a<12）处的某地时，应当选择滴滴打

车还是出租？

(3)请你在如图所示的平面直角坐标系中画出(1)中写出的两个函数图象.

叮/元

20"

15，

10，

力

5，

O123456789.公电

88.为提倡节约用水，我县自来水公司每月只给某单位计划内用水200吨，计划内用

水每吨收费2.4元，超计划部分每吨按3.6元收费.

⑴用代数式表示下列问题(最后结果需化简)：设用水量为x吨，当用水量小于等于

200吨时，需付款多少元？当用水量大于200吨时，需付款多少元？

⑵若某单位4月份缴纳水费840元，则该单位用水量多少吨？

89.如图，直线与反比例函数(x>0)的图象交于A,B两点，已知点A的

X

坐标为(2,4),AAOB的面积为6.

(1)反比例函数的表达式；

(2)求直线的函数表达式；

⑶若动点尸在y轴上运动，当I以一尸8|最大时，求P点坐标.

90.已知，在平面直角坐标系中，点A在)，轴上，OA=a，点且〃、b满足

\Ja+b-8+(a-b-4)2=0.

图1图2

⑴则，，=：b=；

(2)如图1,在x轴上是否存在点C,使三角形ABC的面积等于三角形A3。面积的一

半？若存在，请求出点C的坐标；若不存在，请说明理由；

(3)如图2,将线段AB向左平移〃?个单位(〃?>0),得到线段49,其中点4,点B的

对应点分别为点A,点若点在射线ATT上，连接ON,BN得到三角形

BON,若三角形50N的面积大于三角形A8。面积的3并且小于三角形AB。面积，则

m的取值范围是.

91.已知，关于x的分式方程彳--二=1.

(1)当。=2,6=1时，求分式方程的解；

⑵当4=1时，求匕为何值时分式方程三三一==1无解；

2x4-3x-5

(3)若。=36,且〃、〃为正整数，当分式方程丁J-匚=1的解为整数时，求匕的

2x4-3X-3

值.

92.在两个不全等的三角形中，有两组边对应相等，其中一组是公共边，另一组等边

所对的角对应相等，就称这两个三角形为共边偏差三角形，如图1、AB是公共边、BC

图1图2图3

(1)如图2,在线段AZ)上找一点E,连CE,使得△ACE与4人。。是共边偏差三角形，

并简要说明理由；

(2)在图2中，已知N1=N2,ZB+ZD=180°,求证：△ACB与△4C。是共边偏差三

角形;

(3)如图3,函数丫=立工+2叵的图象与X轴交于点A,与函数y=Gx的图象交于点

33

B,请在坐标轴上找一点尸，使得AABO与AABP是共边偏差三角形，直接写出点P

的坐标.

93.如图，将连续的奇数1,3,5,7,…按图1中的方式排成一个数表，用一个十字

框框柱5个数，这样框出的任意5个数(如图2)分别用“，h,c,d,x表示.

(1)若x=17,贝ija+b+c+d=.

(2)直接写出“，b,c,d,的和与x之间的一个等量关系：.

(3)设/=a+b+c+d+x,判断M的值能否等于2035?若能，请求出框内5个数，

若不能，请说明理由.

2

94.有这样一个问题：探究函数丁=-7-3的图象与性质.小亮根据学习函数的经

x-1

2__

验，对函数y二三-3的图象与性质进行了探究.下面是小亮的探究过程，请补充完

x-1

y八

5-

4-

3-

2-

1-

-5-4-3-2-1O123456x

—1-•

9

(D函数N二口一？中自变量、的取值范围是

(2)表格是y与x的儿组对应值.

_1_2

X-3-2-102345

22

_7_7_5

-7m

y-2-4-5-1-2-3~2

直接写出m的值___________；

(3)在平面直角坐标系xQv中，描出了以上表中各对对应值为坐标的点，根据描出的

点，画出该函数的图象；

(4)根据画出的函数图象，发现下列特征：

①该函数的图象与直线x=l越来越靠近而永不相交，该函数的图象还与直线越

来越靠近而永不相交.

②请再写出此函数的一条性质：.

(5)已知不等式kx+b<^--3的解集为1<x<2或x>4,则左+b的值为.

参考答案:

1.5

【分析】连接0E,根据正方形的性质可得B0=0C=5,再由S480E+SzC0E=S」B0C即可

求得EG+EF的值.

【详解】如图，连接OE,

•••四边形ABC。是正方形，AC=10,

：.AC±BD,BO=OC=5,

'：EGLOB,EFA.OC,S^BOE+SACOE^SABOC,

g•BO-EG+y•OC'EF=1,OB・OC,

：.1x5x£G+1x5xEF=1x5x5,

；.EG+EF=5.

故答案为：5

【点睛】本题考查正方形的性质，利用面积法是解决问题的关键，熟练运用等腰三角形底

边上一点到两腰的距离之和等于腰上的高这一结论可以使运算过程简单.

2.1：24

【分析】根据菱形性质得出ACJ_BD,AB=BC=CD=AD=石，AC=2AO=2CO,

BD=2BO=2DO,即可求出AO：B0,根据勾股定理得出方程，求出x的值，求出AC、

BD,根据菱形面积公式求出即可.

【详解】解：•••四边形ABCD是菱形，

AACIBD,AB=BC=CD=AD=x/5.AC=2AO=2CO,BD=2BO=2DO,

VAC：BD=1：2,

r.AO：BO=1AC：*BD)=AC：BD=1：2；

设AO=x,则BO=2x,

在RtaAOB中，由勾股定理得：x2+(2x)2=(不)2,

答案第1页，共72页

解得：X=1（负数舍去），

即AO=1,B0=2,

；.AC=2,BD=4,

二菱形ABCD的面积是S=^xACxBD=1x2x4=4,

故答案为：1：2,4.

【点睛】本题考查了菱形的性质的应用，主要考查学生运用性质进行推理和计算的能力，

注意：菱形的对角线互相垂直平分，菱形的四条边相等和菱形的面积为两对角线乘积的一

半.

3.22.5°

【分析】根据等边对等角的性质可得/E=/ACE,由正方形的性质得出NBAC=45。，再

由三角形的外角性质即可得出结果.

【详解】解：：AC=AE,

.♦.NE=NACE,

VAC是正方形ABCD的对角线，

AZBAD=90°,ZBAC=45°,

,NE+NACE=45°,

.../ACE=gx45°=22.5°,

故答案为：22.5°.

【点睛】本题考查了正方形的性质，等腰三角形的性质，三角形的外角性质；熟练掌握三

角形的外角性质和正方形的性质是解题的关键.

4.15.

【分析】根据题意，可以计算出黑球的个数，本题得以解决.

【详解】解：由题意可得，黑球有：25X0.6=15（个），

故答案为15.

【点睛】本题考查用样本估计总体，解答本题的关键是明确题意，求出黑球的个数.

5.一次函数正比例函数比例系数

【分析】直接根据一次函数和正比例函数的定义作答即可.

【详解】函数y=H+b（k,b都是常数，且ANO）叫做一次函数，当6=0时，函数＞=日

是常数，k^O）叫做正比例函数，常数k叫做比例系数.

答案第2页，共72页

【点睛】本题考查了一次函数和正比例函数的定义，熟练掌握各知识点是解题的关键.

6.30°

【分析】由题意易得NABC=90。，AB=CD=4,OA=OC=OB=OD,然后根据三角形中位线可

得AC=8,进而根据含30。直角三角形的性质的逆定理可求解.

【详解】解：：四边形ABC。是矩形，CD=4,

二NABC=90°,AB=CD=4,OA=OC=OB=OD,

'：M.N分别是A8、的中点，MN=2,

OB=2MN=4=OA,

：.AC=8,

AB=-AC,

2

ZACB=30°；

故答案为30°.

【点睛】本题主要考查矩形的性质、三角形中位线及直角三角形的性质，熟练掌握矩形的

性质、三角形中位线及直角三角形的性质是解题的关键.

7.73

【分析】根据平行四边形性质推出AB=CD,AB〃CD,得出平行四边形ABDE,推出

DE=DC=AB,根据直角三角形性质求出CE长，即可求出AB的长.

【详解】解：：四边形ABCD是平行四边形，，AB〃DC,AB=CD,

VAE/7BD,二四边形ABDE是平行四边形，；.AB=DE=CD,

即D为CE中点，

VEF1BC,ZEFC=90°,

：AB〃CD,.".ZDCF=ZABC=60°,/.ZCEF=30o,

：EF=3,.*.CE=25

故答案为。.

【点睛】本题考查了平行四边形的性质和判定，平行线性质，勾股定理，直角三角形斜边

上中线性质，含30度角的直角三角形性质等知识点的应用，此题综合性比较强，是一道比

较好的题目.

8.18

【分析】根据直角三角形的性质得到CF=8,根据£尸=1,得到DE=9,根据三角形中位

答案第3页，共72页

线定理解答即可.

【详解】解：：/AF8=90。，点。是48的中点,

：.DF=-AB=S,

：.DE=9,

■:D、E分别是AB,AC的中点,

：.BC=2DE^\S,

故答案为18

【点睛】本题考查的是三角形中位线定理、直角三角形的性质，掌握三角形的中位线平行

于第三边，并且等于第三边的一半是解题的关键.

9.—

12

【分析】由题意可知，共有12个球，取到每个球的机会均等，根据概率公式解题.

【详解】解：P（红球）=看

故答案为：—

【点睛】本题考查简单事件的概率，是基础考点，掌握相关知识是解题关键.

10.4.

【详解】试题分析：设袋中的黑球有X个，根据题意得：—X=4|,解得：x=4,经检

12+x4

验：x=4是原分式方程的解.即袋中的黑球有4个.故答案为4.

考点：概率公式.

11.4石，774•

【分析】（1）.作FHXAB于H,由AAS证明AEFH^ACED,得出FH=CD=4,

AH=AD=4,求出BH=AB+AH=8,由勾股定理即可得出答案；

⑵.求出BM=AB+AM=7,FM=AE+EH=5,由勾股定理即可得出答案.

【详解】（1）作FHLAB于H,如图所示：

答案第4页，共72页

则NFHE=90。，

•.•四边形ABCD和四边形CEFG是正方形,

,AD=CD=4,EF=CE,NADC=NDAH=NBAD=NCEF=90。，

ZFEH=ZCED,

'NFHE=NEDC=90。

在^EFH和小CED中，，NFEH=NCED,

EF=CE

：.AEFH^ACED(AAS),

；.FH=CDH,AH=AD=4,

，BH=AB+AH=8,

,BF=yjBH2+FH2=>/82+42=4石；

(2)过F作FH_LAD交AD的延长线于点H,作FM_LAB于M,如图所示:

则FM=AH,AM=FH,因为BM=AB+AM=4+3=7,FM=AE+EH=5,

,BF=^BM2+FM2=yJl2+52=M.

【点睛】本题考查全等三角形的判定、勾股定理和平行四边形的性质，解题的关键是熟练

掌握全等三角形的判定、勾股定理和平行四边形的性质.

12.黄

【分析】利用频率估计概率得到实验的概率在0.2左右，再求出该字出现的次数，即可解

题.

【详解】解：由折线统计图知，该字出现的频率稳定在数字20%附近，

所以该字出现的概率约为

而“定西的黄土地黄而厚实”一共有10个字，

所以该字的个数为10x1=2

即符合这一结果的试验最有可能抽出的是黄字，

故答案为：黄.

答案第5页，共72页

【点睛】本题考查利用频率估计概率，是基础考点，掌握相关知识是解题关键.

13.三

3

【分析】将（2,--）代入反比例函数解析式，从而可得一次函数解析式，进而求解.

【详解】解：将（2,-=3）代入k得-A：=k

2x22

解得k=-3>

...一次函数解析式为y=-3x+3,

二直线经过第一、二、四象限，

故答案为：三.

【点睛】本题主要考查的是反比例函数及一次函数的基本性质，由待定系数法求出解析

式，根据解析式进行判断是本题的重点.

14.菱

【分析】根据三角形的中位线定理和菱形的判定，顺次连接矩形各边中点所得的四边形是

菱形

【详解】解：如图，连接AC、BD,

■:E、尸、G、，分别是矩形ABCD的AB、BC、CD、AD边上的中点，

:.EF=GH=；AC,FG=EH=，BD,

,/矩形ABCD的对角线AC=B。，

:.EF=GH=FG=EH,

四边形EFGH是菱形.

故答案为：菱.

【点睛】此题主要考查了三角形的中位线定理，矩形的性质和菱形的判定，综合利用了三

角形的中位线定理和矩形的性质是解题关键.

【分析】首先将点A的坐标代入直线关系式，求出机的值，进而得出点A的坐标，设反比

答案第6页，共72页

例函数解析式为卜=",把A的坐标代入求出”的值，即可得出反比例函数关系式.

X

【详解】：该反比例函数的图象与直线y=2x-6的一个交点为A(m,m-2),

**•将点-2)的坐标代入，得加一2=2m—6,解得〃2=4,

・・・点4的坐标为(4,2),

k

设该反比例函数的表达式是y=L贝必=4x2=8,

x

Q

，这个反比例函数的表达式是y=?.

X

Q

故答案为：y=-.

X

【点睛】本题主要考查了反比例函数和一次函数的交点问题，正确得出4点坐标是解题的

关键.

16.k<-1

【分析】根据一次函数的增减性与系数的关系求解即可.

【详解】解：；一次函数y=(Z+l)x-2的函数值y随自变量x的增大而减小，

解得：k<-l.

的取值范围是4<-1.

故答案为：k<-l.

【点睛】本题考查了一次函数的性质，在一次函数丫=丘+6中，当火>0时，y随x的增大

而增大；当％<0时，y随x的增大而减小.

17.5

【分析】把(-L3)代入y=2x+b可得答案.

【详解】解：把(-1,3)代入y=2x+6,

—2+。=3,

b-5,

故答案为：5.

【点睛】本题考查的是待定系数法求解函数解析式中的未知系数，掌握待定系数法是解题

的关键.

答案第7页，共72页

【分析】先根据题意画出树状图，然后根据概率公式进行计算即可.

【详解】解：根据题意画出树状图，如图所示：

开始

012

/N/K

012012012

♦.•有9种等可能的情况数，其中两次抽出的卡片上的数字都是奇数的情况有1种，

，