2023届高考数学二轮复习微专题12立体几何中的平行与垂直问题作业

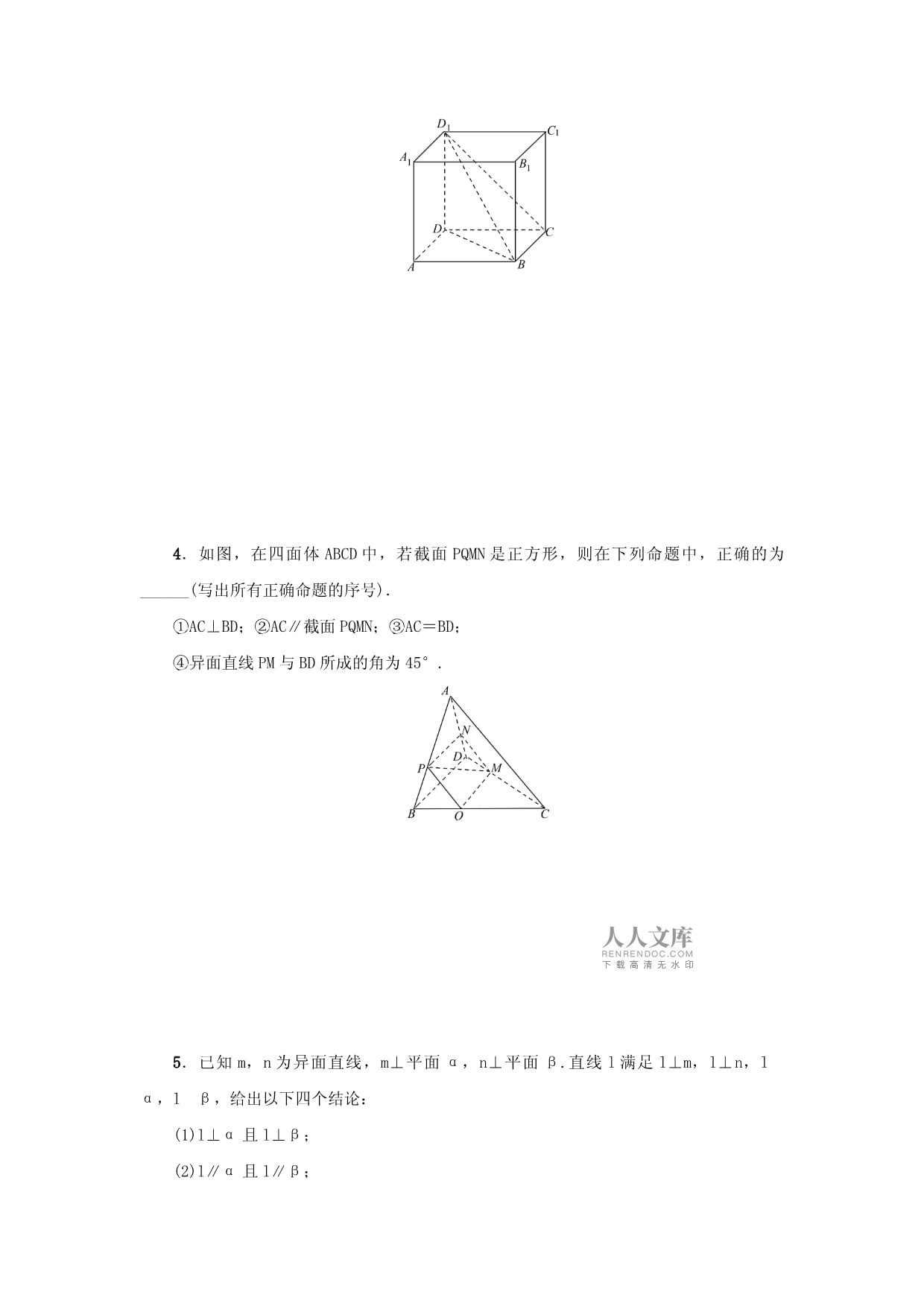
微专题12立体几何中的平行与垂直问题1.设l，m表示直线，m是平面α内的任意一条直线，则“l⊥m”是“l⊥α”成立的________条件(在“充分不必要”“必要不充分”“充要”“既不充分又不必要”中选填一个)．2．α，β为两个不同的平面，m，n为两条不同的直线，下列命题中正确的是________(填上所有正确命题的序号)．①若α∥β，mα，则m∥β；②若m∥α，nα，则m∥n；③若α⊥β，α∩β＝n，m⊥n，则m⊥β；④若n⊥α，n⊥β，m⊥α，则m⊥β.3．如图，在正方体ABCD－A1B1C1D1中，给出以下四个结论：(1)直线D1C∥平面A1ABB1；(2)直线A1D1与平面BCD1相交；(3)直线AD⊥平面D1DB；(4)平面BCD1⊥平面A1ABB1.上述结论中，所有正确结论的序号为________．4．如图，在四面体ABCD中，若截面PQMN是正方形，则在下列命题中，正确的为______(写出所有正确命题的序号)．①AC⊥BD；②AC∥截面PQMN；③AC＝BD；④异面直线PM与BD所成的角为45°.5．已知m，n为异面直线，m⊥平面α，n⊥平面β.直线l满足l⊥m，l⊥n，lα，lβ，给出以下四个结论：(1)l⊥α且l⊥β；(2)l∥α且l∥β；(3)α与β相交，且交线垂直于l；(4)α与β相交，且交线平行于l.上述结论中所有正确结论的序号为________．6．如图，矩形ABCD中，E为边AB的中点，将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点，则在△ADE翻转过程中，其中正确命题的序号为________．①|BM|是定值；②点M在球上运动；③一定存在某个位置，使DE⊥A1C；④一定存在某个位置，使MB∥平面A1DE.

7.如图，等边三角形ABC与直角梯形ABDE所在平面垂直，BD∥AE，BD＝2AE，AE⊥AB，M为AB的中点．(1)证明：CM⊥DE；(2)在边AC上找一点N，使CD∥平面BEN.8．如图，在直三棱柱ABC－A1B1C1中，点D，E分别在边BC，B1C1上，CD＝B1E＝eq\f(1,2)AC，∠ACD＝60°.求证：(1)BE∥平面AC1D；(2)平面ADC1⊥平面BCC1B1.微专题121．答案：充要．解析：因为m是平面α内的任意一条直线，若l⊥m，则l⊥α，所以充分性成立；反过来，若l⊥α，则l⊥m，所以必要性成立，故“l⊥m”是“l⊥α”成立的充要条件．2．答案：①④.解析：①中，由面面平行的性质可知，故①正确；②中，若m∥α，nα，则m∥n或m与n异面，故②不正确；③中，若α⊥β，α∩β，m⊥n，则有可能发生mβ的情况，故③不正确；④中，若n⊥α，m⊥α，则m∥n，又n⊥β，则m⊥β，故④正确．3．答案：(1)(4)．解析：(1)中，D1C平面A1ABB1，且D1C∥A1B；A1B平面A1ABB1，所以D1C∥平面A1ABB1，故(1)正确；(2)中A1D1平面BCD1，所以不正确；(3)中AD与DB不垂直，又因为DB平面D1DB，所以不正确；(4)中BC⊥平面A1ABB1，且BC平面BCD1，所以平面BCD1⊥平面A1ABB1，故(4)正确．4．答案：①②④.解析：在四面体ABCD中，因为截面PQMN是正方形，所以PN∥QM，PN平面ABD，QM平面ABD，所以QM∥平面ABD，又BD平面ABD，所以QM∥BD，同理PQ∥AC，由PQ⊥QM，所以AC⊥BD，故①正确；由PQ∥AC，PQ截面PQMN，AC截面PQMN，所以AC∥截面PQMN，故②正确；因为截面PQMN是正方形，直线PM与QM所成的角为45°，又BD∥QM，故异面直线PM与BD所成的角为45°，故④正确；AC与BD不一定相等，故③不正确．5．答案：(2)(4)．解析：由m⊥平面α，直线l满足l⊥m，且lα，lα，则l∥α，同理可证l∥β.所以(2)正确，(1)错误．由直线m，n为异面直线，且m⊥平面α，n⊥平面β，则α与β相交，否则，若α∥β，则推出m∥n，与m，n异面矛盾．故α与β相交，且交线平行于l.所以(4)正确，(3)错误．6．答案：①②④.解析：如图，取DC中点N，连接MN，NB，则MN∥A1D，NB∥DE，所以平面MNB∥平面A1DE，因为MB平面MNB，所以MB∥平面A1DE，④正确；∠A1DE＝∠MNB，MN＝eq\f(1,2)A1D为定值，NB＝DE为定值，根据余弦定理得，MB2＝MN2＋NB2－2MN·NB·cos∠MNB，所以MB是定值．①正确；B是定点，所以M是在以B为圆心，MB为半径的球上，②正确；当矩形ABCD满足AC⊥DE时存在，其他情况不存在，③不正确．所以①②④正确．7．证明：(1)因为BC＝AC，M为AB中点，所以CM⊥AB，又平面ABC⊥平面ABDE，平面ABC∩平面ABDE＝AB，CM平面ABC，所以CM⊥平面ABDE，又DE平面ABDE，所以CM⊥DE.(2)当eq\f(AN,AC)＝eq\f(1,3)时，CD∥平面BEN.如图，连结AD交BE于点K，连结KN.因为在梯形ABDE中，BD∥AE，BD＝2AE，所以eq\f(AK,KD)＝eq\f(AE,BD)＝eq\f(1,2)，则eq\f(AK,AD)＝eq\f(1,3).又eq\f(AN,AC)＝eq\f(1,3)，所以KN∥CD.因为KN平面BEN，CD平面BEN，所以CD∥平面BEN.8．证明：(1)由三棱柱ABC－A1B1C1是直三棱柱，得BC∥B1C1且BC＝B1C1.因为点D，E分别在边BC，B1C1上，CD＝B1E，所以BD＝C1E且BD∥C1E.所以四边形BDC1E是平行四边形，所以BE∥C1D.因为C1D平面AC1D，BE平面AC1D，所以BE∥平面AC1D.(2)由三棱柱ABC－A1B1C1是直三棱柱，得CC1⊥平面ABC.因为AD平面ABC，所以AD⊥CC1.在△ACD中，CD＝eq\f(1,2)AC，∠ACD＝60°，所以由余弦定理，可知AD＝eq\r(AC2＋CD2－2AC·CDc