微分方程的物理背景

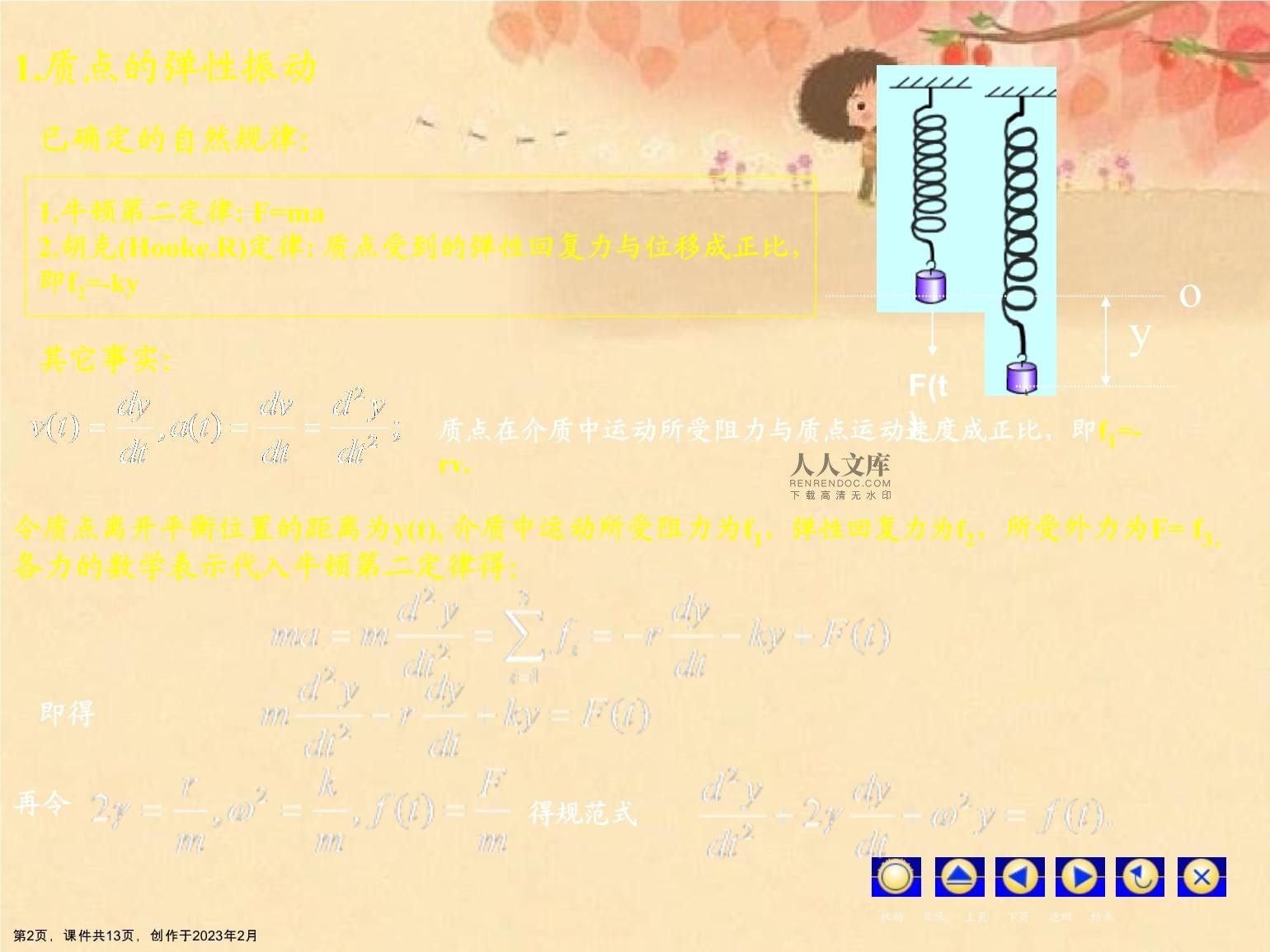
微分方程的物理背景第1页，课件共13页，创作于2023年2月1.质点的弹性振动机动目录上页下页返回结束F(t)yo已确定的自然规律：1.牛顿第二定律:F=ma

2.胡克(Hooke.R)定律:质点受到的弹性回复力与位移成正比，即f2=-ky其它事实：质点在介质中运动所受阻力与质点运动速度成正比，即f1=-rv.令质点离开平衡位置的距离为y(t),介质中运动所受阻力为f1，弹性回复力为f2，所受外力为F=f3，各力的数学表示代入牛顿第二定律得：即得再令得规范式第2页，课件共13页，创作于2023年2月特例1：真空中落体运动机动目录上页下页返回结束当r=k=0,即介质阻尼与弹性约束为0，且F=mg,则微分方程为再若t=0时，v(0)=v0,y(0)=y0则得特例2：简谐振动当r=0，F=0,则微分方程为可以验证方程的解为第3页，课件共13页，创作于2023年2月机动目录上页下页返回结束2.RLC交变电路CRU(t)L已确定的事实：1.欧姆定律：2.楞次定律:3.Kirchhoff定律:其它事实：令电流i=i(t)，电阻的电势降uR=uR(t)，电感的电势降uL=uL(t)，电容的电势降uC=uC(t)，电容电荷Q=Q(t)，电路输入电压U=U(t),根据Kirchhoff定律有即得再令得规范式※这说明有阻尼的机械振动与RLC电路，其运动变化机理，在数学上是统一的。第4页，课件共13页，创作于2023年2月机动目录上页下页返回结束机动目录上页下页返回结束3.冷却与衰变例1.1一温度为500℃的物体置于20℃的环境中，2分钟后温度降为400℃，问10分钟后温度降至多少？冷却定律：物体温度下降速率和物体与环境温差成正比令温度为T=T(t),将冷却定律表示成数学形式即得其中k为比例常数，从而得t与T的微元关系两边积分得根据初始数据t=0,T=500以及t=2,T=400即得C=480,在表达式中代入t=10得第5页，课件共13页，创作于2023年2月第二节目录上页下页返回结束例1.2放射性衰变已确定规律：放射性物质的放射速率与质量本身成正比令放射性物质的质量为m=m(t),将放射律表示成数学形式即得其中k为比例常数，从而得t与m的微元关系两边积分得令初始数据为t=t0,m=m0即得从而放射过程为第6页，课件共13页，创作于2023年2月机动目录上页下页返回结束机动目录上页下页返回结束4.人口增长（1）马尔萨斯人口律：若人口的生存环境宽松，食物充裕，则其增长率与人口基数成正比。设某地区人口总数为N=N(t),由马尔萨斯人口律得从而得t与N的微元关系两边积分得令初始数据t=t0,N=N0即得第7页，课件共13页，创作于2023年2月（2）Logistic人口律：在人口群体中，由于生存竞争而产生一个与人口平方成正比的负增长率。设某地区人口总数为N=N(t),由Logistic律得令a<<b,N(t0)=N0解得otNN0第8页，课件共13页，创作于2023年2月5.溶液淡化例1.3.容器内有100升浓度10﹪的盐溶液，若以3升/秒的匀速往容器中注入净水，同时又以2升/秒的速度将搅匀后的溶液排出，问过程开始后1分钟时溶液的浓度？溶液淡化是一不均匀的过程，须用微元法来分析！设时刻为t时溶液的含盐量为x=x(t),任选时间微元区间[t,t+dt],由于dt充分小，因此微元时间间隔内过程可视为均匀的。根据微分的定义即得根据厨师数据x(0)=10,即得溶液淡化的数学模型：求解后得：，1分钟后，浓度为第9页，课件共13页，创作于2023年2月6.二体运动（行星绕日运动）Kepler三律（被称为“太空宪法”）：（A）行星绕日运动轨道是椭圆，太阳是轨道的一焦点上；（B）太阳与行星的连线（经线）在相同时间间隔内扫过相同的面积；（C）行星公转周期的平方与它到太阳平均距离的立方成正比。精确解释建立行星绕日运动的数学模型万有引力定律：行星受到太阳的引力f与矢径r的平方成反比，与行星质量m与太阳质量M的乘积成正比，引力方向与矢径方向相反。运用牛顿第二定律，表示成数学表达式得：其中ur表示单位矢径。第10页，课件共13页，创作于2023年2月xPoɵ令这里表示动点P的极坐标此时矢径为记表示矢径方向的单位向量，表示与矢径正交的单位矢量则有如下关系式：令v=v(t)表示U(t)的瞬时速度，则有令a=a(t)表示v(t)的瞬时加速度，则有简记则有第11页，课件共13页，创作于2023年2月代入牛顿第二定律得由于两个单位向量的正交性即得这就是二体运动方程——由极坐标表示的行星绕日运动的微分方程。第12页，课件共13页，创作于2023年2月试建立具有下列性质的曲线满足的微分方程。1，曲线上任意点的切线与该点的径向夹角为。2，曲线上任意点的切线介