向量加法运算及其几何意义课件

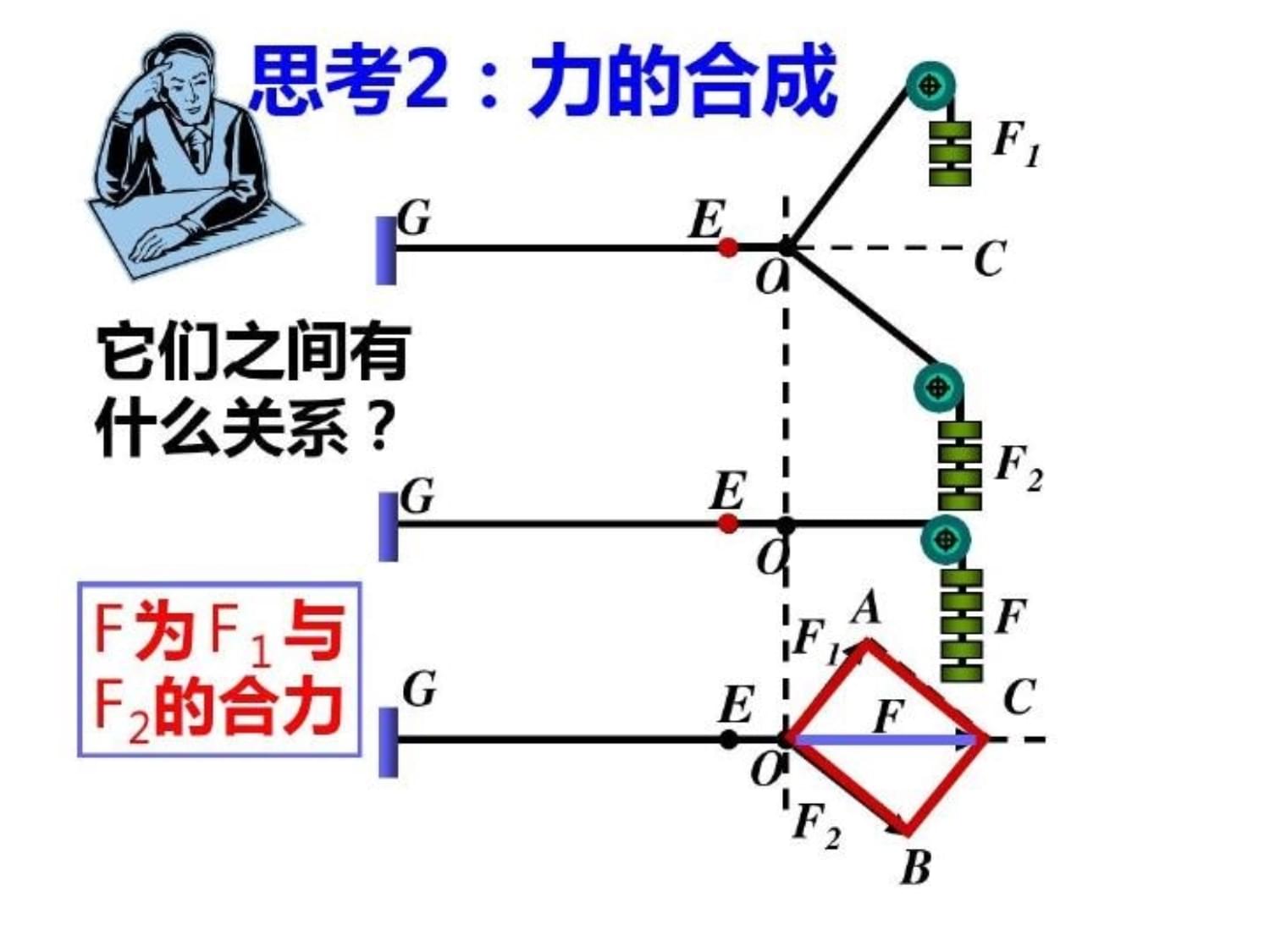
向量加法运算及其几何意义向量加法运算及其几何意义向量加法运算及其几何意义既有大小又有方向的量是否可以相加呢?两个实数可以相加,从而给数赋予了新的内涵如果向量仅停留在概念的层面上,那是没有多大意义的我们希望两个向量也能相加,拓展向量的数学意义,提升向量的理论价值,这就需要建立相关的原理和法则思考1:位移的合成如图某人从点A到点B,再从点B改变方向到点C,则两次位移的和可用什么来表示?由此可得什么结论?AB+BC=AcB上述分析表明,位移的合成可看作是向量的加法。培养学生高尚的道德情操和健康的审美情趣，形成正确的价值观和积极的人生态度，是语文教学的重要内容。成功的写作教学不仅是教会学生写作技巧，更重要的是教会学生做人，是对学生心理的同化，情感的培养，人格的塑造。在教学实践中，我注意了言为心声、文道统一，在写作教学始终渗透情感目标。一、在感受中教会关爱写作的素材源于生活，教师首先要教会学生热爱生活。培养学生以健康的心理走向生活，感受生活。把学生带进大自然，带进社会，带进实实在在的人生，让他们学会发现，学会关心，学会热爱，学会奉献，为学生设置一个激发热情的情境，这样，他们才会主动去捕捉，去汲取，去思考，去领悟，作文也就有了不竭之源。初春的原野，孩子们在挖荠菜吃荠菜中感受到了春之生机与自由；深冬的雪地里，孩子们在堆雪人打雪仗中领悟到冬之无暇与博大；对小流域环境污染的调查，让同学们感悟到环境恶化的警钟离我们不再遥远；帮助比自己更需要帮助的人，使同学们体味到爱心温暧足以点燃世界……把作文与做人结合起来，让学生感到只要关心社会，关注自我，思考人生，就随时有东西可写，有感情可发，从而更激发热爱生活、感悟生活的热情。二、在选材中倡导真情学生正在成长的过程中，生活阅历浅，性格在发展变化中，渴望独立，但往往犹豫不定，力不从心，不可能准确地认识自己，评估自己。他们面对太多的压力，太多的困惑，太多的疑问。做人如此，作文亦如此。反映在他们的文章中缺少独特的个性，内容没有深刻的体验，真实性不强，文章反映的思想常显得幼稚肤浅，文章语言仅有华丽的词藻。还有，专制虚假的社会语言环境，不良的社会现象，使学生写出的文章少年老成，空话套话假话，甚至人格和道德上的缺憾。他们太需要老师用真实去建立真实，用健康的情感去培养健康的情感，培养学生正确的人生观与价值观，加强学生的心理教育，培养学生用审美直觉对生活深层理解。同学间的小小争执；对家人的腹诽；学农基地劳动时，孩子们不肯割去地中间的一片玉米杆，他们担心其间结巢的那只小鸟找不到家；甚至日记中流露出的一些真实而稚气的情绪（如某生做梦打好友小霞和老师，问梦为何故，师谐批曰“日有所思，夜有所梦”，生续批“非也，即便想过，也没想过要打小霞”，话外之意，憨笑可掬！）……这些，都及时予以肯定和引导，这些，也都成了后来习作中的一个个亮点！三、在表达中张扬个性写作不只是一种表达技巧，它是极具个性化和创造性的精神活动。写作中，贯穿始终的是写作主体的个性化的脑力劳动，个性永远是写作的主宰。教师必须把学生从习惯化，共性化的观察、感知和思维状态中引导出来，引导他们从个性化的角度去表达自我，吐露真情。张扬个性，要有意识的引导学生从不同角度去认识、理解生活，避开别人易思考的角度，摆脱习惯性思考，求新求活。鼓励学生个性化语言，注意锤炼字词，巧用修辞，独创妙语佳句，力求含蓄风趣。张扬个性，教师要努力营造一种和谐宽松的写作氛围，激发学生思维尤其是创新思维，尊重和强化主体意识，由于阅历和素养的差异，学生在作文上表现出来为多样性，只有承认学生的差异，尊重学生的个性，学生才会用自己特有的方式表达独特见解，进而形成自己的风格。四、在评改中培养品质主观意识的培养是写作教学的根本。作文的立意、选材、谋篇、布局无不是学生主观意识的表现。所以在学生作文评改时，教师要换位思考，重视学生反馈心态。评改中，褒多于贬，鼓励多于批评，给学生更多的成功体验，激发他们对作文的兴趣，发挥其巨大潜能，尽力挖掘学生的每一个闪光点。重视培养学生独立的思维品质和个性品质，处理好模仿与创新、求同与求异的关系，积极鼓励学生的创新精神，力争写出的文章有个性，要从作文的结构、语言、基本观点、思想感情、文风和写作态度等方面，权衡得失，分析利弊，以明确的态度中肯评价。最后，教学的成功源自于教师的人格感召力。很难相信，一名教师，志大才疏、思想平庸、为人粗俗，能成为学生为人为文的导师。这是我的育人观，也是我的做人观。电子技术基础课程是由模拟电子技术、模拟电子实验、数字电子技术等部分组合而成，这是一个理论与实践并重的课程，也是电子信息技术专业学生的基础课程，电子信息技术对培养全方位人才发挥着重要作用。一、电子信息技术专业日常教学存在的问题电子信息技术专业作为新时期的热门专业，受到社会各界的广泛关注，强化对电子信息专业课程的教学，对培养适应现代化社会需求的人才发挥着重要作用。然而，某些高等院校在电子信息技术专业课程的日常教学中，存在一些有待解决的问题，严重影响本专业人才的质量和学习效率。具体表现在以下方面：通常情况下，电子信息专业入学前两学年安排较少的课程，但在第三学年一般会安排大量的课程，这种课程设置情况对学生保持紧张的学习氛围非常不利，会在一定程度上影响学生的实践，致使学生实践操作能力不强。学生自行选择选修课程时，院校及本专业老师没有对学生给予合理的指导，致使学生选的专业毫不相关，缺乏系统性的学习。同时，学生的自学能力比较差，学生学习的内容仅仅局限在教科书上，缺乏把书本知识灵活应用到实践中的锻炼机会。二、电子信息技术专业课程教学的优化改进1改革传统教学方法将传统的“填鸭式”“满堂灌”的教学模式，转变为以“学生的发展为根据”的教学方式，广泛使用启发式、讨论式、参与式等不同的教学方法，从而做好“设计问题”“引导反思”“探索求证”等步骤。同时，帮助学生形成正确的思维方式，促使学生有能力使用已经学习的知识解决实际问题。并锻炼学生发现问题、分析问题、解决问题再学习的能力。教学课程上，老师应把课本上最基本的理论知识和分析方法传授给学生，让学生具有一定的自学能力。对学生进行全面的跟踪，及时掌握学生的学习状态，课程前后实施教学辅导，积极开展教学调查，时时进行教学反思。2及时更新教学内容一个称职的老师不能只循规蹈矩、按部就班地照着原本的计划、教学大纲讲述一门课或几门课程，缺乏自己的创新思维和创造性工作，恐怕不是现代理念上的好老师。如：在对“信号与系统”课程进修教学时，把基础知识服务于应用中，无法脱离应用学习过的理论知识，关于理论知识需要结合应用展开学习。在研究学生培养目标的时候，重视实际应用，重视培养学生的能力。日常教学通常列举实际的应用问题，达到知识的转化。随着科学技术的快速发展，必须积极参与科学研究，更新教学内容及组织体系，只有如此，才能满足时代发现，贴近学生的特点并满足社会需求。讲授教学课程时，学生不单单要熟悉本门课程，也要了解、熟悉有关的课程。电子技术课程教学理论知识信息量极大，随着计算机技术和半导体器件的不断发展，新技术、新器件与教学内容相互融合和渗透促使教学内容、实践内容不断更新。实际教学时，坚决剔除教材内某些过时的知识，对新型实用的内容进行补充。3合理设计课程题目教学课程作为学生学完某一专业课程后实践教学的重要环节，也是培养学生使用本课程理论知识与及时解决问题的课程，在一定程度上是提升使用技术资料、设计能力的重要环节，在日常实践中发挥着重要作用。每一学期通常开设两门专业基础或专业的课程设计。老师应该精心选择课题，最好把本课程学习的知识与实际问题有效结合，同时可以涵盖部门以前学过的知识，培养学生使用所学知识解决问题的能力。课程设计通常安排在课程结束后的一周时间内，时间太紧，学生有可能无法在短时间内对整个设计项目和实施过程有完整的了解。所以，老师上课的时候要提前向学生提交课程设计的题目，为学生指明需要设计的知识点，教会学生如何查找资料。总之，对高等院校电子信息技术课程体系实施改革与优化，是势在必行。对电子信息技术专业课程的优化设计，不仅能有效提高专业课程的教学质量与效率，也能在某种程度上提升电子信息技术专业学生的实践能力，培养出满足社会发展需求的高素质人才。既有大小又有方向的量是否可以相加呢?两个实数可以相加,从而给数赋予了新的内涵如果向量仅停留在概念的层面上,那是没有多大意义的我们希望两个向量也能相加,拓展向量的数学意义,提升向量的理论价值,这就需要建立相关的原理和法则向量的加法:BC起连a+b点对相角O以同一点O为起点的两个向量a、b为邻边作平行四边形OACB则以O为起点的对角线OC就是c与b的和即a+b=OA+OB=OC我们把这种作两个向量和的方法叫做向量加法的平行四边形法则对于零向量与任一向量a,我们规定a+0=0+d=对于向量的加法的理解需要注意下面两点:(1)两个向量的和仍然是向量简称和向量)(2)位移的合成是三角形法则的物理模型力F的分解为平行四边形法则三角形法则:首尾相接连端点平行四边形法则:起点相同连对角例1如图,已知向量a,b求作向量a+b。作法1:在平面内任取一点O作OA=a,AB=b,则OB=a+b。Aa+三角形法则例1如图,已知向量a,h求作向量a+b。作法2:在平面内任取一点O作OA=a,OB=b以OA,OB为邻边作平行四边形OACB,连结OC则OC=OA+OB=a+ba+bB练习P84第1,2,3题平行四边