沪科版圆周角

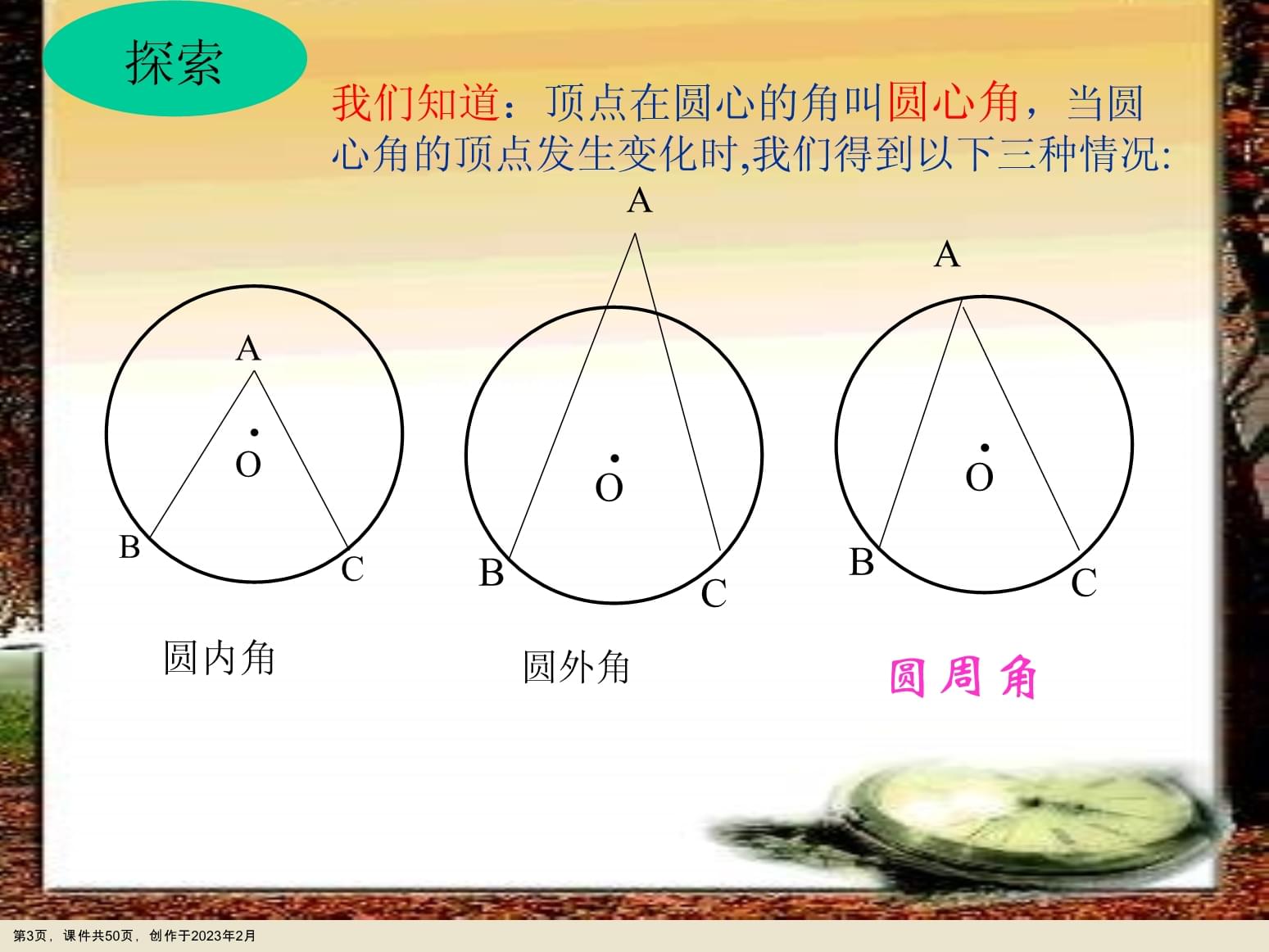
关于沪科版圆周角第1页，课件共50页，创作于2023年2月一.复习引入:1.圆心角的定义?.OBC在同圆（或等圆）中，如果圆心角、弧、弦、弦心距有一组量相等，那么它们所对应的其余两个量都分别相等。答:顶点在圆心的角叫圆心角2.上节课我们学习了一个反映圆心角、弧、弦、弦心距四个量之间关系的一个结论，这个结论是什么？第2页，课件共50页，创作于2023年2月探索1:我们知道：顶点在圆心的角叫圆心角，当圆心角的顶点发生变化时,我们得到以下三种情况:A.OBC.OBCA.OBCA圆内角圆外角圆周角探索第3页，课件共50页，创作于2023年2月oABC考考你：你能仿照圆心角的定义，给下图中象∠ACB这样的角下个定义吗？顶点在圆上，并且两边都和圆相交的角叫做圆周角．

第4页，课件共50页，创作于2023年2月

顶点在圆上，并且两边都和圆相交的角．什么叫做圆周角？·ABCDEO二、概念第5页，课件共50页，创作于2023年2月辩一辩图中的∠CDE是圆周角吗?CDECDECDECDE第6页，课件共50页，创作于2023年2月6．5圆周角（一）练习一：判断下列各图中，哪些是圆周角，为什么？

oABoABoABoABoABoABoABoABoABCCCCCCCC图1图2图3图4图5图6图7图8图9第7页，课件共50页，创作于2023年2月如图是一个圆柱形的海洋馆的横截面的示意图,人们可以通过其中的圆弧形玻璃AB观看窗内的海洋动物,同学甲站在圆心的O位置，同学乙站在正对着玻璃窗的靠墙的位置C，他们的视角（∠AOB和∠ACB）有什么关系？如果同学丙、丁分别站在他靠墙的位置D和E，他们的视角（∠ADB和∠AEB

）和同学乙的视角相同吗？二、观察第8页，课件共50页，创作于2023年2月深入探究１．视角∠AOB和∠ACB有什么关系？即同弧所对的圆心角和圆周角的关系．２．∠ADB和∠AEB和∠ACB相等吗？即同弧所对的圆周角之间的大小关系．第9页，课件共50页，创作于2023年2月类比圆心角探知圆周角在同圆或等圆中,同弧或等弧所对的圆心角相等.在同圆或等圆中,同弧或等弧所对的圆周角有什么关系？

为了解决这个问题,我们先探究同弧所对的圆周角和圆心角之间有的关系.你会画同弧所对的圆周角和圆心角吗?第10页，课件共50页，创作于2023年2月圆周角和圆心角的关系在⊙O任取一个圆周角∠BCA，将圆对折，使折痕经过圆心O和∠BCA的顶点C。由于点C的位置的取法可能不同，这时有三种情况：（1）折痕是圆周角的一条边，如图（1）（2）折痕在圆周角的内部，如图（2）

（3）折痕在圆周角的外部．如图（3）

第11页，课件共50页，创作于2023年2月圆周角和圆心角的关系1.首先考虑一种特殊情况：当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.∵∠AOC是△ABO的外角，∴∠AOC=∠B+∠A.∵OA=OB，●OABC∴∠A=∠B.∴∠AOC=2∠B.即∠ABC=∠AOC.根据以上证明你能得到什么结论？

第12页，课件共50页，创作于2023年2月(1)圆心在圆周角的一边上证明：∵OA=OC∴∠BAC＝∠C∴∠BOC＝∠BAC+∠C=2∠BAC∴∠BAC=∠BOC定理证明第13页，课件共50页，创作于2023年2月2.考虑第二种情况当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?

能否转化为1的情况?过点B作直径BD.由1可得:●O∴∠ABC=∠AOC.根据以上证明你又能得到什么结论？ABCD∠ABD=∠AOD,∠CBD=∠COD,圆周角和圆心角的关系第14页，课件共50页，创作于2023年2月(2)圆心在圆周角的内部证明：连结AO并延长交⊙O于D点D∠ＣAＤ=∠ＣOＤ由（１）得∠BAＤ=∠BOＤ∴∠BＡC＝∠BＯＣ∴∠BＡC＝∠BＯＤ+∠CＯＤ))))第15页，课件共50页，创作于2023年2月圆周角和圆心角的关系3.考虑第二种情况当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?能否也转化为1的情况?过点B作直径BD.由1可得:●OD∠ABD=∠AOD,∠CBD=∠COD,ABC∴∠ABC=∠AOC.根据以上证明你又能得到什么结论？第16页，课件共50页，创作于2023年2月(３)圆心在圆周角的外部证明：连结AO并延长交⊙O于D点D∠ＣAＤ=∠ＣOＤ由（１）得∠BAＤ=∠BOＤ∴∠BＡC＝∠BＯＣ∴∠BＡC＝∠ＣＯＤ－∠ＢＯＤ))))第17页，课件共50页，创作于2023年2月三.圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半。思考：在同圆或等圆中，如果圆周角相等，所对的弧一定相等吗？定理归纳.ABCDO弧等角等第18页，课件共50页，创作于2023年2月结论：

在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．相等的圆周角所对的弧也相等。圆周角定理第19页，课件共50页，创作于2023年2月考眼力如图,点A、B、C、D在同一个圆上，四边形ABCD的对角线把4个内角分成8个角，这些角中哪些是相等的角？∠1=∠4∠2=∠7∠3=∠6∠5=∠8★★★★★★★★第20页，课件共50页，创作于2023年2月思考如图，线段AB是⊙O的直径，点C是⊙O上任意一点（除点A、B），那么，∠ACB就是直径AB所对的圆周角，想想看，∠ACB会是怎样的角？OCBA90°的圆周角所对的弦是什么?

半圆（或直径）所对的圆周角是直角;90°的圆周角所对的弦是直径．推论第21页，课件共50页，创作于2023年2月·ABC1OC2C3定理

在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．相等的圆周角所对的弧也相等。定理

半圆（或直径）所对的圆周角是直角;90°的圆周角所对的弦是直径．推论第22页，课件共50页，创作于2023年2月CODBA如图：圆内接四边形ABCD中，∵∠BAD等于弧BCD所对圆心角的一半,∠BCD等于弧BAD所对圆心角的一半.而弧BCD所对的圆心角+弧BAD所对的圆心角=360°，∴∠BAD＋∠BCD＝180°.

同理∠ABC＋∠ADC＝180°.圆内接四边形的对角互补.四边形与圆的位置关系第23页，课件共50页，创作于2023年2月如果延长BC到E，那么∠DCE＋∠BCD＝180°.∴∠A＝∠DCE.又∵∠A＋∠BCD＝180°，CODBAE四边形与圆的位置关系因为∠A是与∠DCE相邻的内角∠DCB的对角,我们把∠A叫做∠DCE的内对角.圆内接四边形的一个外角等于它的内对角.第24页，课件共50页，创作于2023年2月试金石：2.如图，圆心角∠AOB=100°，则∠ACB=___。OABCBAO.70°x1.求圆中角X的度数C第25页，课件共50页，创作于2023年2月3、如图AB是⊙O的直径,C,D是圆上的两点,若∠ABD=40°,则∠BCD=＿＿＿＿＿.ABOCD40°第26页，课件共50页，创作于2023年2月4.如图：OA、OB、OC都是⊙O的半径，且∠AOB=2∠BOC.求证：∠ACB=2∠BAC.AOBC第27页，课件共50页，创作于2023年2月5⑴如图5，求∠1＋∠2＋∠3＋∠4＋∠5=

。⑵如图6：已知弦AB、CD相交于P点，且∠AOC=44、∠BOD=46求∠APC的度数。12345图5OABCDP图6第28页，课件共50页，创作于2023年2月例1如图，⊙O直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于D，求BC、AD、BD的长．又在Rt△ABD中，AD2+BD2=AB2，解：∵AB是直径，∴∠ACB=∠ADB=90°．在Rt△ABC中，∵CD平分∠ACB，∴AD=BD.四、例题第29页，课件共50页，创作于2023年2月求证：如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形．（提示：作出以这条边为直径的圆.）·ABCO求证：△ABC

为直角三角形.证明：CO=AB,以AB为直径作⊙O，∵AO=BO， ∴AO=BO=CO.∴点C在⊙O上.又∵AB为直径,∴∠ACB=×180°=90°.已知：△ABC中，CO为AB边上的中线，且CO=AB∴△ABC

为直角三角形.练习第30页，课件共50页，创作于2023年2月练习:如图AB是⊙O的直径,C,D是圆上的两点,若∠ABD=40°,则∠BCD=＿＿＿＿＿.ABOCD40°第31页，课件共50页，创作于2023年2月3、AB、AC为⊙O的两条弦，延长CA到D，使AD=AB，如果∠ADB=35°

，求∠BOC的度数。∠BOC=140°350700第32页，课件共50页，创作于2023年2月交流合作１.ΔABC内接于⊙O，∠BOC=80º，则∠BAC等于().(A)80º(B)40º(C)140º(D)40º或140ºＤ第33页，课件共50页，创作于2023年2月交流合作２．已知:如图,AB=AC=AD,∠BAC=40º,则∠BDC的度数为()（A）40º

（B）30º（C）20º

（D）不能确定ABCDＣ第34页，课件共50页，创作于2023年2月交流合作15°或75°3．在半径为1的⊙O中，弦AB、AC分别是则∠BAC的度数为＿＿＿＿＿．第35页，课件共50页，创作于2023年2月交流合作4．如图，⊙O1、⊙O2相交于A、B两点，直线O1O2交两圆于C、D∠O1AO2=40°，则∠CBD等于（）（A）110°（B）120°（C）130°（D）140°A第36页，课件共50页，创作于2023年2月课堂反馈1．如图，已知圆心角∠BOC＝100°，则圆周角∠BAC的度数为（）A、100°B、130°C、50°D、80°2．圆内接正三角形的一条边所对的圆周角为()A、30°B、60°C、30°或150°D、60°或120°3．如图，A、B、C三点在⊙O上，∠AOC=100°，则∠ABC等于()A、140°B、110°C、120°D、130°CＤＤ第37页，课件共50页，创作于2023年2月课堂反馈4.若圆的一条弦把圆分成度数的比为1∶3的两条弧，则劣弧所对的圆周角的度数为（）A、45°

B、90°

C、135°

D、270°5．已知：如图，△ABC内接于⊙O，AD是⊙O的直径，∠ABC＝30°，则∠CAD等于_________。6．在⊙O中，一条弦的长度等于半径，则它所对的圆周角的度数为_________。7．半径为1的圆中有一条弦，如果它的长为那么这条弦所对的圆A周角的度数等于

.60°60°或120°30°或150°第38页，课件共50页，创作于2023年2月弦AB分圆为l∶5两部分，则弦AB所对的圆周角度数等于

9．已知：如图，AB为⊙O的直径，∠BED=35º，则∠ACD=

º。10．圆内接四边形相邻三个内角之比是3:1:6，则这个四边形的最大角的度数为

。ODABCE30°或150°55160°课堂反馈第39页，课件共50页，创作于2023年2月7学以致用作业适量分层要求A层（基础题）

⑶如图9，已知AB=AC=2cm,∠BDC=60，则△ABC的周长是

。

⑷如图10：∠A是⊙O的圆周角，∠A=40°，求∠OBC的度数。ABCDO图9ABCO图10第40页，课件共50页，创作于2023年2月7学以致用作业适量分层要求B层（中等题）

⑴在⊙O中，∠BOC=100o，则弦BC所对的圆周角是

度。

⑵如图11，AD是⊙O直径，BC=CD，∠A=30°，求∠B的度数。

ABCDO图11第41页，课件共50页，创作于2023年2月7学以致用作业适量分层要求C层（提高题）

如图12，AB是⊙O直径，点C在圆上，∠BAC的平分线交圆于点E，OE交BC于点H，已知AC=6，AB=10，求HE的长。ABCOHE图12第42页，课件共50页，创作于2023年2月7

学以致用作业适量分层要求D层（课外延拓、承上启下）

如图13：“世界杯”赛场上李铁、邵佳一、郝海东三名队员互相配合向对方球门进攻，当李带球冲到如图C点时，邵、郝也分别跟随冲到图中的D点、E点，李应把球传给谁好？请你从数学角度帮忙合情说理、分析说明。ABCDEO图13球门第43页，课件共50页，创作于2023年2月能力提升

1、在⊙O中，∠CBD=30°,∠BDC=20°,求∠A第4