尺规作图三等分角_第1页
尺规作图三等分角_第2页
尺规作图三等分角_第3页
尺规作图三等分角_第4页
尺规作图三等分角_第5页
已阅读5页，还剩5页未读， 继续免费阅读

下载本文档

版权说明：本文档由用户提供并上传，收益归属内容提供方，若内容存在侵权，请进行举报或认领

文档简介

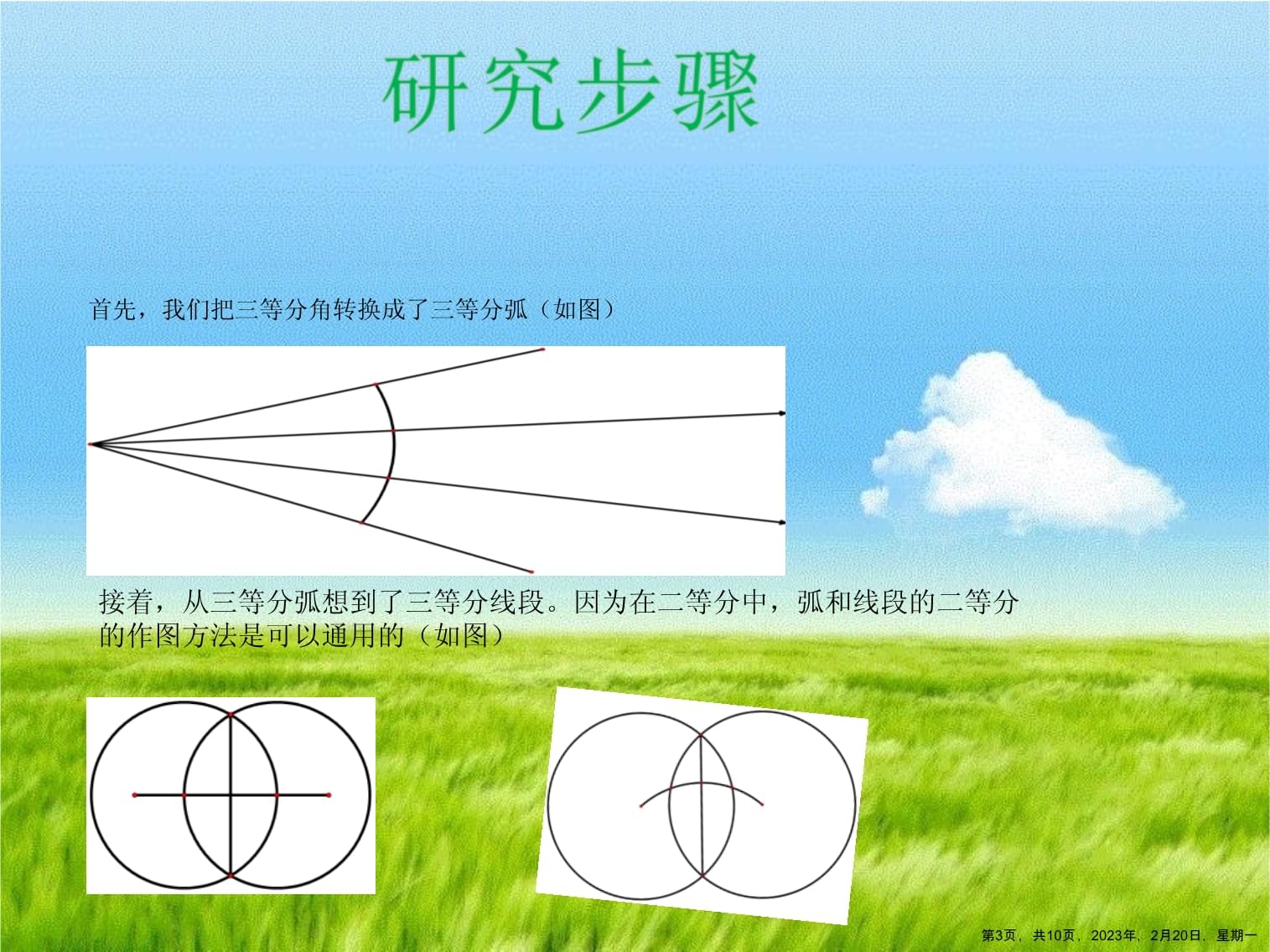
尺规作图三等分角第1页，共10页，2023年，2月20日，星期一这次我们组的数学课题是“如何用尺规作图三等分一个角”。这个问题在世界上都很有知名度，据说用了许多方法都没能做出来。所以我们的目的自然不是做出答案，而是训练培养组员多方面多角度地考虑问题，会用多种方法解决问题。也培养了组员思考的逻辑性和严谨性，提高画图能力，体会研究的乐趣。下面是我们组的研究成果。这里一定有仍需完善的地方，我们会根据大家的提议进行修改。第2页，共10页，2023年，2月20日，星期一首先，我们把三等分角转换成了三等分弧（如图）接着，从三等分弧想到了三等分线段。因为在二等分中，弧和线段的二等分的作图方法是可以通用的（如图）第3页，共10页，2023年，2月20日，星期一所以我们一共想了两种三等分线段的方法：1.2.第4页，共10页，2023年，2月20日，星期一但是我们发现，二等分中，弧和线段之所以能用同一种方法分割，是因为他们的分割线是他们的对称轴。如果把线段的端点和弧的端点重合，那么它们的对称轴即分割线重合。换一种说法，其实我们分的是弧对应的弦。碰巧的是，在二等分中，它们正好重合，所以它们才能用同一种方法（如图）而三等分则不然。弦的三等分并不是弧的三等分（如图）第5页，共10页，2023年，2月20日，星期一弧的三等分与线段的三等分点的连线应该不是平行的。于是我们又开始研究弧、弦与圆心角的关系。可是他们之间并不存在，或者只有很复杂的关系，所以并不能通过弦与圆心角来画出弧的三等分。但是我们又想到了π。π约等于三，所以在圆上，可以粗略地把圆周三等分（如图）这样，只要求出所求角度与360°的关系，再把圆规的半径缩小到同一倍数，也能近似的三等分一个角。但是，这个方法受许多限制，比如在缩小倍数时不能保证完全精确，使本已近似的结果误差更大。有时倍数也不能太复杂。所以，只有特殊角的三等分可以用这种办法的。第6页，共10页，2023年，2月20日，星期一

之后，我们又查了各种资料，又了解了一种三等分角的办法。虽说都不是标准的尺规作图，但是仍然很精确：1、设所求角为角ACB，并延长AC（如图）第7页，共10页，2023年，2月20日，星期一2、以C为圆心，BC为半径画半圆（如图）然后，在直尺上做刻度OP，长度为AC。使O在射线AC上移动，P在圆上移动。当O、P、B三点共线时，连接PC（如图）第8页，共10页，2023年，2月20日，星期一

如此作图，∠PCO=∠ACB/3（只需把∠PCO复制到∠ACB上即可）这个图虽然精确，但在尺子上做了标记，不是很标准。以上就是我们组的研究成果，其中有些不妥当之处，望大家及时

人人文库> 全部分类> 教育资料 > 课件下载

温馨提示

  • 1. 本站所有资源如无特殊说明，都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
  • 2. 本站的文档不包含任何第三方提供的附件图纸等，如果需要附件，请联系上传者。文件的所有权益归上传用户所有。
  • 3. 本站RAR压缩包中若带图纸，网页内容里面会有图纸预览，若没有图纸预览就没有图纸。
  • 4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
  • 5. 人人文库网仅提供信息存储空间，仅对用户上传内容的表现方式做保护处理，对用户上传分享的文档内容本身不做任何修改或编辑，并不能对任何下载内容负责。
  • 6. 下载文件中如有侵权或不适当内容，请与我们联系，我们立即纠正。
  • 7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

最新文档

评论

0/150

提交评论