线性离散系统振动理论的应用

关于线性离散系统振动理论的应用第一页，共五十二页，2022年，8月28日5.1单自由度系统阻尼比和固有频率的确定

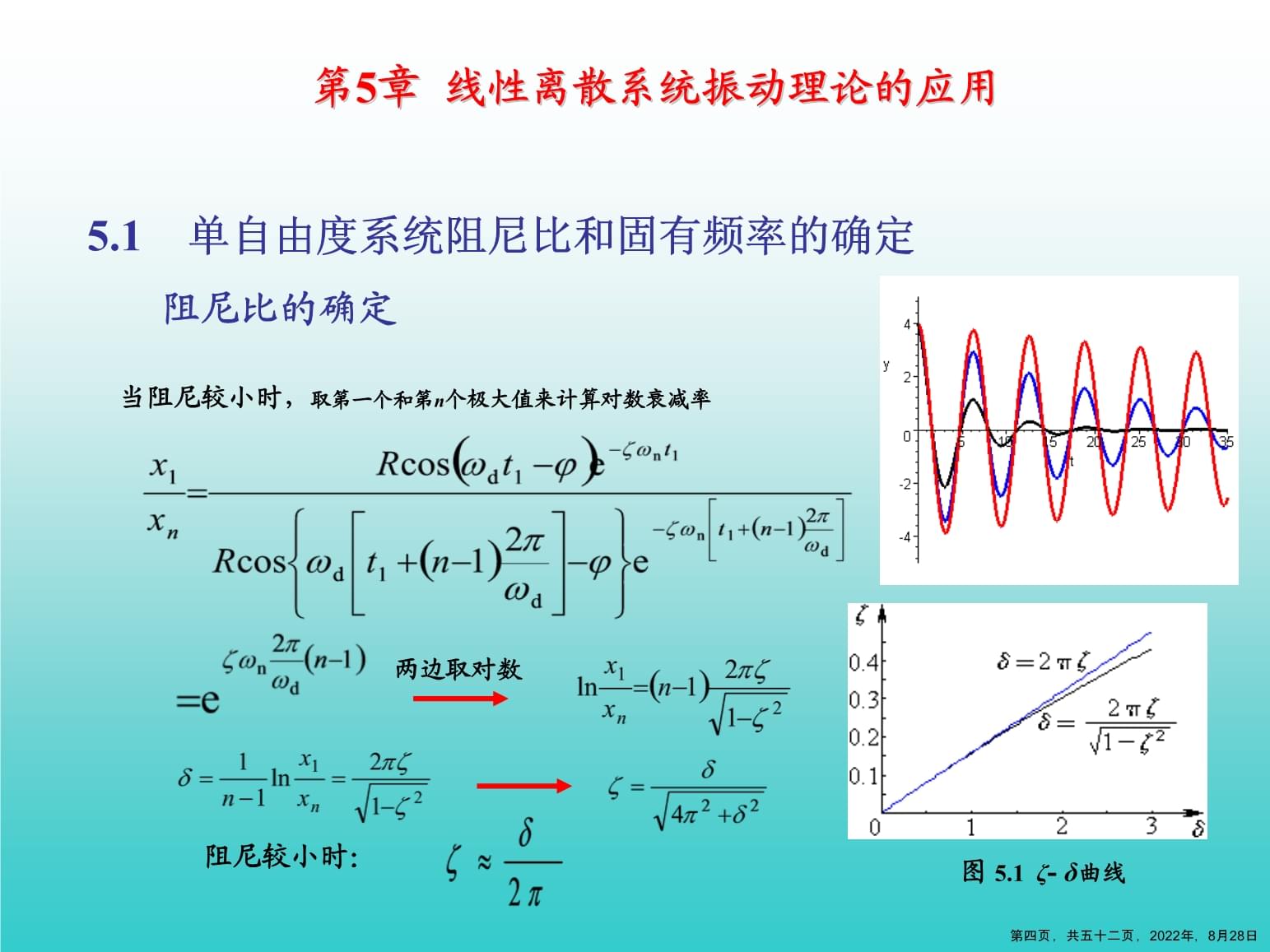
阻尼比的确定第5章线性离散系统振动理论的应用对于阻尼未知的系统或阻尼特性未知的材料组成的单自由度系统，给定初始扰动后测定其自由振动的时间历程，当阻尼较小时，一般可等效为具有粘性阻尼的系统。图3.6弱阻尼系统x-t

曲线

的极值发生位置1、对数衰减率第二页，共五十二页，2022年，8月28日5.1单自由度系统阻尼比和固有频率的确定

出现一次极值，出现一次极大值。相邻两个极大值之比(衰减率)为

对数衰减率为

阻尼比的确定第5章线性离散系统振动理论的应用第三页，共五十二页，2022年，8月28日5.1单自由度系统阻尼比和固有频率的确定当阻尼较小时，取第一个和第n个极大值来计算对数衰减率阻尼较小时：

图5.1ζ-δ曲线两边取对数阻尼比的确定第5章线性离散系统振动理论的应用第四页，共五十二页，2022年，8月28日5.1单自由度系统阻尼比和固有频率的确定2、面积法

自由振动衰减曲线的包络线为

在t1时间中上包络线与坐标轴之间的面积A为：两边同除

0.0200.1040.2150.3340.4640.6060.7610.9341.260.990.950.900.850.800.750.700.650.601.3341.5941.8852.2322.6573.1973.7564.9655.2350.550.500.450.400.350.300.250.200.19

与无因次面积的关系

阻尼比的确定第5章线性离散系统振动理论的应用第五页，共五十二页，2022年，8月28日5.1单自由度系统阻尼比和固有频率的确定计算步骤：

2)作上包络线；

3)选作图得到面积A，并计算；

4)查表5-1得；5)计算阻尼比：

1)测得自由振动衰减曲线；当t1为n倍准周期时，就是对数衰减率。ARt1阻尼比的确定第5章线性离散系统振动理论的应用第六页，共五十二页，2022年，8月28日5.1单自由度系统阻尼比和固有频率的确定固有频率的确定

测量第一个和第n+1个极大值出现的时间间隔nτd

，例1

某系统自由振动衰减曲线中相邻的四个极大值分别为：x1=11.8mm,x2=10mm,x3=8.475mm,x4=7.182mm,t4-t1=0.6s。求系统的阻尼比和固有圆频率。

解：(1)阻尼比：

第5章线性离散系统振动理论的应用第七页，共五十二页，2022年，8月28日5.1单自由度系统阻尼比和固有频率的确定面积法：n

=4

(2)固有圆频率：

固有频率的确定第5章线性离散系统振动理论的应用第八页，共五十二页，2022年，8月28日5.1单自由度系统阻尼比和固有频率的确定1、共振法位移、速度、加速度响应幅值达到最大值时系统发生共振。当激励频率等ω于ωd或ωn时系统发生共振。当响应的相位角滞后激励力的相位角时系统发生共振。在位移、速度和加速度响应幅值保持不变而激励力幅值最小时系统发生共振。图5.2F-ω曲线固有频率的确定共振的定义第5章线性离散系统振动理论的应用第九页，共五十二页，2022年，8月28日5.1单自由度系统阻尼比和固有频率的确定

共振(ω=ωn)时

如果能测得ω=ωn时的X0，并已知此时激励力幅值F0与弹簧刚度k，则阻尼比或损耗因子

Q因子

共振时系统最大动能或位能与系统每循环耗散能量之比的倍称为Q因子。共振时粘性阻尼每循环耗能：固有频率的确定第5章线性离散系统振动理论的应用第十页，共五十二页，2022年，8月28日5.1单自由度系统阻尼比和固有频率的确定共振时最大动能与最大势能相等

对粘性阻尼对结构阻尼通过测试手段获得每周期耗能及共振振幅固有频率的确定第5章线性离散系统振动理论的应用第十一页，共五十二页，2022年，8月28日5.1单自由度系统阻尼比和固有频率的确定2、半功率带宽法

当激励频率变化时，可得到曲线

为曲线的最大值，曲线上的点1、2

半功率带宽

幅频响应曲线半功率点与1、2点对应的频率为和，频率差固有频率的确定第5章线性离散系统振动理论的应用第十二页，共五十二页，2022年，8月28日5.1单自由度系统阻尼比和固有频率的确定1.对具有粘性阻尼的系统

由半功率点的定义

固有频率的确定第5章线性离散系统振动理论的应用第十三页，共五十二页，2022年，8月28日当时，可略去，，由幂级数展开公式()：5.1单自由度系统阻尼比和固有频率的确定固有频率的确定第5章线性离散系统振动理论的应用第十四页，共五十二页，2022年，8月28日2.对结构阻尼系统

由半功率点的定义或5.1单自由度系统阻尼比和固有频率的确定固有频率的确定第5章线性离散系统振动理论的应用第十五页，共五十二页，2022年，8月28日5.2旋转失衡

振动微分方程

设广义坐标为机器的位移x，向上为正，坐标原点在机器静平衡时转子的旋转中心o。

旋转失衡力学模型转子质心位移为加速度为对结构阻尼整理第5章线性离散系统振动理论的应用第十六页，共五十二页，2022年，8月28日5.2旋转失衡

设解对结构阻尼第5章线性离散系统振动理论的应用第十七页，共五十二页，2022年，8月28日5.2旋转失衡幅频和相频响应曲线讨论：相位角同简谐激励下的响应，而无量纲振幅随无量纲频率的变化如下表。粘性阻尼结构阻尼旋转失衡谐激励最大值位置01

0

0

0

1

1

旋转失衡

谐激励第5章线性离散系统振动理论的应用第十八页，共五十二页，2022年，8月28日5.2旋转失衡

例2

偏心激振器两轴反向旋转，每个偏心轮旋转失衡为4.5kg-cm，用它测量结构的动力特性。设结构质量为160kg，激振器质量为20kg。当偏心轮转速为900rpm，偏心质量在正上方时，结构向上通过静平衡位置，振幅为2.5cm。

求1)整个系统的固有圆频率；

2)结构的固有圆频率和阻尼比（或损耗因子）；

3)偏心轮转速为1200rpm时结构的振幅及结构向上通过平衡位置时，偏心质量与水平面的夹角。

偏心激振器模型第5章线性离散系统振动理论的应用第十九页，共五十二页，2022年，8月28日5.2旋转失衡解：方程

M=20+160=180kg，me=4.5kg-cm稳态响应为

偏心质量在正上方，即，结构向上通过静平衡位置，则有，，。

（系统），

粘性阻尼：第5章线性离散系统振动理论的应用第二十页，共五十二页，2022年，8月28日5.2旋转失衡结构阻尼：

2)

，，

粘性阻尼：

结构阻尼：

第5章线性离散系统振动理论的应用第二十一页，共五十二页，2022年，8月28日5.2旋转失衡3)当转速为1200rpm时：

粘性阻尼:

结构阻尼：

粘性阻尼:第5章线性离散系统振动理论的应用第二十二页，共五十二页，2022年，8月28日5.2旋转失衡结构阻尼：

结构通过平衡位置：粘性阻尼:

结构阻尼:第5章线性离散系统振动理论的应用第二十三页，共五十二页，2022年，8月28日5.3旋转轴的临界转速质心位移为：微分方程为：

直立单盘转子

设特解为

第5章线性离散系统振动理论的应用第二十四页，共五十二页，2022年，8月28日5.3旋转轴的临界转速，

设距离为

导前的相位角当时，R接近最大值，把与旋转轴横向振动固有圆频率相当的转速称为旋转轴的临界转速。第5章线性离散系统振动理论的应用第二十五页，共五十二页，2022年，8月28日5.3旋转轴的临界转速

轴在不同转速下的相位：

圆盘质心G与几何中心的相对位置轴以角速度绕过点的轴心线旋转，而过点的轴心线又以角速度绕过点的支承点连线转动，方向相同，这称为旋转轴同步正回旋。在临界转速时，轴上的应力不发生变化，这与不转的轴系在简谐激励下的共振有本质的区别（轴应力交变）。在临界转速时轴心偏离平衡位置的距离达到最大值，也称为共振。阻尼又较小时，接近，因此与重合，称为自动定心。

第5章线性离散系统振动理论的应用第二十六页，共五十二页，2022年，8月28日5.3旋转轴的临界转速例3

某试验台转子质量M为100kg，轴直径=100mm

，弹性模量E

=2.1×1011N/m2，密度。求转轴的临界转速。(实质是求转子横向振动的固有圆频率，然后转换成转速。)解：(1)求等效系统：

1)用定义求ke：在轴中央加一个力F

，位移为x，单盘转子

2)：

第5章线性离散系统振动理论的应用第二十七页，共五十二页，2022年，8月28日5.3旋转轴的临界转速设轴振动时振型与静挠度曲线相同，处的位移为，轴作弯曲振动时沿轴上各点的位移可用表示：系统等效前后的动能分别为：第5章线性离散系统振动理论的应用第二十八页，共五十二页，2022年，8月28日5.3旋转轴的临界转速(2)轴系横向振动的固有圆频率：(3)临界转速：

第5章线性离散系统振动理论的应用第二十九页，共五十二页，2022年，8月28日5.4隔振原理

隔振：在振源和机器或结构等物体之间用弹性或阻尼装置连接，以减小振源对其它物体的影响。主动隔振：减小振动系统对外界的影响。被动隔振：减小外界振源对设备的影响。力传递率(主动隔振)设机器的位移x为广义坐标，向下为正，静平衡时位移为零。方程为：

通过弹簧和阻尼器传递的力

第5章线性离散系统振动理论的应用第三十页，共五十二页，2022年，8月28日5.4隔振原理

通过弹簧与阻尼器传给地面的动态力幅为弹簧力和阻尼力的矢量和。定义：力传递率S

对粘性阻尼：

传递率随无量纲频率的变化第5章线性离散系统振动理论的应用第三十一页，共五十二页，2022年，8月28日5.4隔振原理

对结构阻尼：

当阻尼可忽略时：讨论：

结论：

1)当时，，无隔振效果，振动可能放大；2)当时，，有隔振效果；3)，，即当时，同样的频率比，系统的阻尼比越小隔振效果越好。

第5章线性离散系统振动理论的应用第三十二页，共五十二页，2022年，8月28日5.4隔振原理例4

转速为3000rpm、旋转失衡为0.1kg-m、质量为68kg的电机，安装在1200kg的隔振机座上。系统的固有频率为26.67Hz，阻尼比为ζ＝0.1。求：1)隔振机座的振幅；

2)通过隔振机座传递到地面的力幅。解：

机座的振幅为：

第5章线性离散系统振动理论的应用第三十三页，共五十二页，2022年，8月28日5.4隔振原理讨论：

思考：若系统阻尼增加，如何变化？

，，，。

第5章线性离散系统振动理论的应用第三十四页，共五十二页，2022年，8月28日5.4隔振原理

位移传递率(被动隔振)基础激励

设底座位移为y，质量为m的设备位移为广义坐标x。底座不动，系统静平衡时设备的位置为广义坐标的原点，方向如图.

粘性阻尼:振动微分方程为：结构阻尼:

第5章线性离散系统振动理论的应用第三十五页，共五十二页，2022年，8月28日5.4隔振原理设底座位移为，系统质量的位移为粘性阻尼结构阻尼粘性阻尼第5章线性离散系统振动理论的应用第三十六页，共五十二页，2022年，8月28日5.4隔振原理

结构阻尼定义：位移传递率S粘性阻尼第5章线性离散系统振动理论的应用第三十七页，共五十二页，2022年，8月28日5.4隔振原理结构阻尼定义：隔振效率

隔振模型例5

精密仪器-橡胶隔振系统中，，，地面简谐运动规律为，，

=0.1256mm/s。求：精密仪器位移的最大值和隔振效率。第5章线性离散系统振动理论的应用第三十八页，共五十二页，2022年，8月28日5.4隔振原理解：隔振效率第5章线性离散系统振动理论的应用第三十九页，共五十二页，2022年，8月28日5.4隔振原理

测振仪测振仪利用了基础激励下相对运动与原运动的关系系统振动微分方程为：

设，则相对位移，

第5章线性离散系统振动理论的应用第四十页，共五十二页，2022年，8月28日5.4隔振原理1、位移测量：

时，，2、速度测量：利用电路输出电压：3、加速度测量：第5章线性离散系统振动理论的应用第四十一页，共五十二页，2022年，8月28日5.5动力吸振器无阻尼动力吸振器无阻尼动力吸振器稳态响应第5章线性离散系统振动理论的应用第四十二页，共五十二页，2022年，8月28日5.5动力吸振器当

时，，

第5章线性离散系统振动理论的应用第四十三页，共五十二页，2022年，8月28日

5.5动力吸振器这时传给的力为

作用于上的激励力与由弹簧传给的力恰好抵消，因而。设第5章线性离散系统振动理论的应用第四十四页，共五十二页，2022年，8月28日5.5动力吸振器设：，，令可得到，（二自由度的固有频率）。第5章线性离散系统振动理论的应用第四十五页，共五十二页，2022年，8月28日5.5动力吸振器无量纲响应随无量纲频率变化的曲线曲线μ1-η和曲线μ2-η当η=1，即ω=ω1=ω2时才能使μ1=0，从而X2=0。当η稍偏离1.0，|X1|就很快增，因而当动力吸振器设计好后，只要激励频率略有偏离，原系统的响应就会增加。因此，只有当单自由度系统受单一频率激励力作用时，才能设计一个无阻尼动力吸振器来抑制系统的响应。第5章线性离散系统振动理论的应用第四十六页，共五十二页，2022年，8月28日5.5动力吸振器阻尼动力吸振器η、υ、μ和同(5-35)设阻尼动力吸振器第5章线性离散系统振动理论的应用第四十七页，共五十二页，2022年，8月28日5.5动力吸振器阻尼动力吸振器主系统幅频响应曲线设式(5-39)

中的参数=1.0，=0.05，分别取为0.32、0.1和0，曲线从图中看，尽管取不同的阻尼比时不同，但这些曲线