数学实验8-曲线拟合

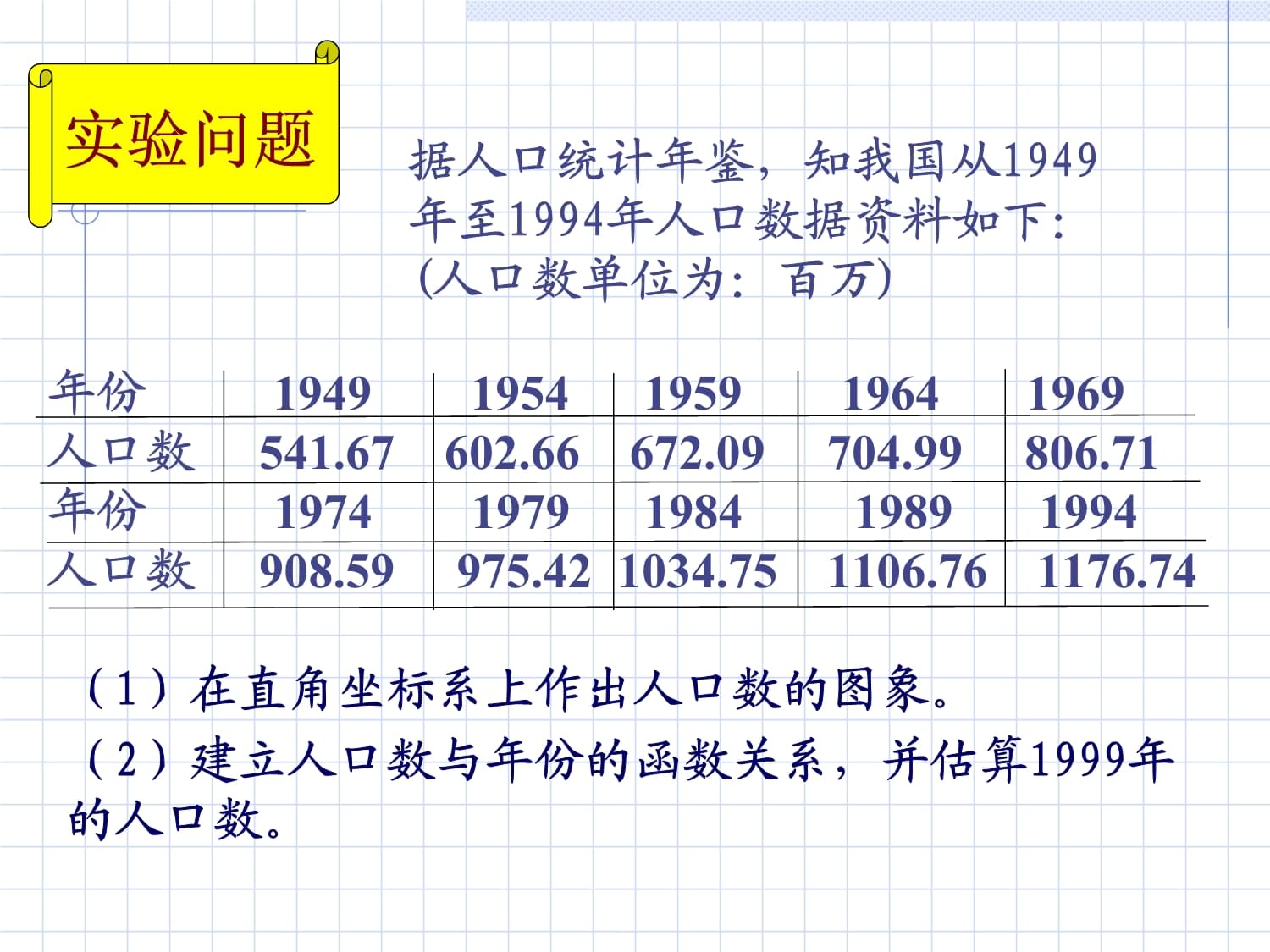
MathematicsLaboratory阮小娥博士ExperimentsinMathematics李换琴数学实验办公地址：理科楼225电话：82663174实验13人口数量预测模型实验2、掌握在最小二乘意义下数据拟合的理论和方法.1、学会用MATLAB软件进行数据拟合3、通过对实际问题的分析和研究，初步掌握建立数据拟合数学模型的方法实验目的据人口统计年鉴，知我国从1949年至1994年人口数据资料如下：(人口数单位为：百万)（1）在直角坐标系上作出人口数的图象。（2）建立人口数与年份的函数关系，并估算1999年的人口数。实验问题年份

1949

1954

1959

1964

1969

人口数

541.67

602.66

672.09704.99

806.71

年份1974

1979

1984

1989

1994人口数

908.59

975.421034.75

1106.76

1176.74

如何确定a,b?线性模型1曲线拟合问题的提法:

已知一组（二维）数据，即平面上的n个点),(iiyx，

ixni,,,2,1L=互不相同，寻求一个函数（曲线）)(xfy=，使)(xf在某种准则下与所有数据点最为接近，即曲线拟合得最好，如图:

xy0++++++++一、曲线拟合确定f(x)使得

达到最小

最小二乘准则

２.用什么样的曲线拟合已知数据?常用的曲线函数系类型：１．画图观察；２．理论分析指数曲线：

双曲线（一支):

多项式：

直线：

３拟合函数组中系数的确定二、人口预测线性模型

对于开始提出的实验问题,代如数据，计算得从而得到人口数与年份的函数关系为把x=1999代如，估算出1999年的人口数为y=1252.1（百万）＝12.52亿1999年实际人口数量为１２.６亿。线性预测模型英国人口学家Malthus根据百余年的人口统计资料，于1798年提出了著名的人口自然增长的指数增长模型。三、人口预测的Malthus模型基本假设

:人口(相对)增长率r

是常数x(t)~时刻t的人口,t=0时人口数为x0指数增长模型实际中，常用1.由前100年的数据求出美国的人口增长Malthus模型。2.预测后100年（每隔10年）的人口状况。3.根据预测的人口状况和实际的人口数量,讨论人口模型的改进情况。美国1790年－1980年每隔10年的人口记录226.5204.0179.3150.7131.7123.2106.592.076.062.9人口(百万)1980197019601950194019301920191019001890年份50.238.631.423.217.112.99.67.25.33.9人口(百万)1880187018601850184018301820181018001790年份例１解：取得最小值.其中,表示人口数量。表示年份,解方程组:即得参数的值.使得问题转化为求参数％prog41.m%%Thisprogramistopredictthenumberofpopulation%formatlongt1=[1790;1800;1810;1820;1830;1840;1850;1860;1870;1880];t2=[1890;1900;1910;1920;1930;1940;1950;1960;1970;1980];x1=[3.9;5.3;7.2;9.6;12.9;17.1;23.2;31.4;38.6;50.2];x2=[62.9;76.0;92.0;106.5;123.2;131.7;150.7;179.3;204.0;226.5];lnx1=log(x1);lnx2=log(x2);a12=sum(t1);a11=10;a21=a12;a22=sum(t1.^2);d1=sum(lnx1);d2=sum(lnx1.*t1);

A=[a11,a12;a21,a22];D=[d1;d2];

ab=inv(A)*D;

disp('a=');disp(ab(1));

disp('b=');disp(ab(2));

fori=1:10

xx1(i)=exp(ab(1)+ab(2)*t1(i));

end

fori=1:10

xx2(i)=exp(ab(1)+ab(2)*t2(i));

end

plot(t1,x1,'r*--',t1,xx1,'b+-',t2,x2,'g*--',t2,xx2,'m+-');

a=-49.79535457790735b=0.02859807120038仿真结果表明：人口增加的指数模型在短期内基本上能比较准确地反映人口自然增长的规律，但长期预测误差很大，需要修正预测模型。拟合曲线原始数据曲线四、人口预测的Logistic模型人口增长到一定数量后，增长率下降的原因：资源、环境等因素对人口增长的阻滞作用且阻滞作用随人口数量增加而变大假设r~固有增长率(x很小时)k~人口容量（资源、环境能容纳的最大数量）r是x的减函数例１的Logistic模型留给同学们练习五、多项式拟合的Matlab指令a=polyfit（xdata，ydata，n）其中n表示多项式的最高阶数

xdata，ydata为要拟合的数据，它是用向量的方式输入。输出参数a为拟合多项式

y=a1xn+…+anx+an+1的系数a=[a1,…,an,an+1]。多项式在x处的值y可用下面程序计算。

y=polyval(a,x)

用多项式拟合人口模型%Thisprogramistopredictthemodelofpopulationby4-degreepolynomial%%prog42.m%formatlongt1=[1790;1800;1810;1820;1830;1840;1850;1860;1870;1880];t2=[1890;1900;1910;1920;1930;1940;1950;1960;1970;1980];t=[t1;t2];P1=[3.9;5.3;7.2;9.6;12.9;17.1;23.2;31.4;38.6;50.2];P2=[62.9;76.0;92.0;106.5;123.2;131.7;150.7;179.3;204.0;226.5];P=[P1;P2];n=4;%Thedegreeofthefittingpolynomial%[a,s]=polyfit(t1,P1,n);y=polyval(a,t);%aisthecoefficientsvectorfromn-degreeto0-degree%plot(t,P,'r*--',t,y,'b+-');23a=1.0e+006*-0.000000000000140.00000000107892-0.000003048785950.00381927346813-1.79012132225427仿真结果表明,人口增加的模型用多项式拟合能比较准确地反映人口自然增长的规律，对长期预测具有指导意义。例2:海底光缆线长度预测模型某一通信公司在一次施工中,需要在水面宽为20m的河沟底沿直线走向铺设一条沟底光缆.在铺设光缆之前需要对沟底的地形做初B2468101214161820986420ADC探测到一组等分点位置的深度数据如下表所示.25步探测,从而估计所需光缆的长度,为工程预算提供依据.基本情况如图所示.10.9310.809.818.867.957.959.1510.2211.2912.6113.32201918171615141312111013.2812.2611.1810.139.058.027.967.968.969.01深度(m)9876543210分点21个等分点处的深度(1)预测通过这条河沟所需光缆长度的近似值.(2)作出铺设沟底光缆的曲线图.解：用12次多项式函数拟合光缆走势的曲线图如下仿真结果表明,拟合曲线能较准确地反映光缆的走势图.Thelengthofthelabelis

L=26.3809(m)假设所铺设的光缆足够柔软,在铺设过程中光缆触地走势光滑,紧贴地面,并且忽略水流对光缆的冲击.%prog45.mThisprogramistofitthedatabypolynomial%formatlongt=linspace(0,20,21);x=linspace(0,20,100);P=[9.01,8.96,7.96,7.97,8.02,9.05,10.13,11.18,12.26,13.28,13.32,12.61,11.29,10.22,9.15,7.90,7.95,8.86,9.81,10.80,10.93];[a,s]=polyfit(t,P,12);yy=polyval(a,x);plot(x,yy,'r*--',t,P,'b+-');L=0;fori=2:100L=L+sqrt((x(i)-x(i-1))^2+(yy(i)-yy(i-1))^2);enddisp('ThelengthofthelabelisL=');disp(L);formatlongt=linspace(0,20,21);x=linspace(0,20,100);P=[9.01,8.96,7.96,7.97,8.02,9.05,10.13,11.18,12.26,13.28,13.32,12.61,11.29,10.22,9.15,7.90,7.95,8.86,9.81,10.80,10.93];n=input(‘n=’)%通过键盘输入拟合次数[a,s]=polyfit(t,P,n);yy=polyval(a,x);p1=polyval(a,t);d=norm(P-p1)%计算拟合误差plot(x,yy,'r*--',t,P,'b+-');L=0;fori=2:100L=L+sqrt((x(i)-x(i-1))^2+(yy(i)-yy(i-1))^2);enddisp('ThelengthofthelabelisL=');disp(L);x0x1x2x3x4xg(x)实验14插值问题

f(x)插值函数有各种类型，如代数多项式，三角函数，有理函数等。当p(x)为多项式时，称为（代数）插值多项式。一阶二阶三阶由克莱姆法则知方程组有唯一解，即满足(1.1)的插值多项式存在且唯一。Matlab指令：yb=interp1(x,y,xb,’method’)详见课本204页实验任务:观测序号12345678910X46495152545657585960Y40505563727077739093观测序号11121314151617181920X61626364666768717271Y9688991101131201271371321371、下表中，X是华氏温度，Y是一分钟内一只蟋蟀的鸣叫次数，试用多项式模型拟合这些数据，画出拟合曲线，分析你的拟合模型是否很好？2、(1)在下列数据中，W表示一条鱼的重量，l表示它的长度，使用最小二乘准则拟合模型W=kl3长度l（英寸）14.512.517.2514.512.62517.7514.12512.625重量w（盎司）

2717412617492316(2)**

在下列数据中，g表示一条鱼的身围，使用最小二乘准则拟合模型W=k