高中物理人教版第三章相互作用5力的分解

教学准备1.

教学目标知识与技能1．知道什么是力的分解，了解力的分解的一般方法．2．知道平行四边形定则和三角形定则都是矢量运算法则．3．能用平行四边形定则和三角形定则进行矢量运算．过程与方法1．通过设置问题，启发学生的思考，启迪学生的物理思维．2．通过组织探究实验，训练学生明辨是非、格物致理的能力．情感态度与价值观1．通过组织探讨和探究实验，培养学生的合作精神，使学生体会到在交流中可以提高自己的能力．2．让学生初步体会到物理学的和谐美和统一美．3．通过分析实际问题，激发学生的学习兴趣．2.

教学重点/难点教学重点1．平行四边形定则和三角形定则在力的分解中的应用．2．根据力的作用效果对力进行分解．3．正交分解法．教学难点应用平行四边形定则和三角形定则进行矢量运算．3.

教学用具多媒体、板书4.

标签

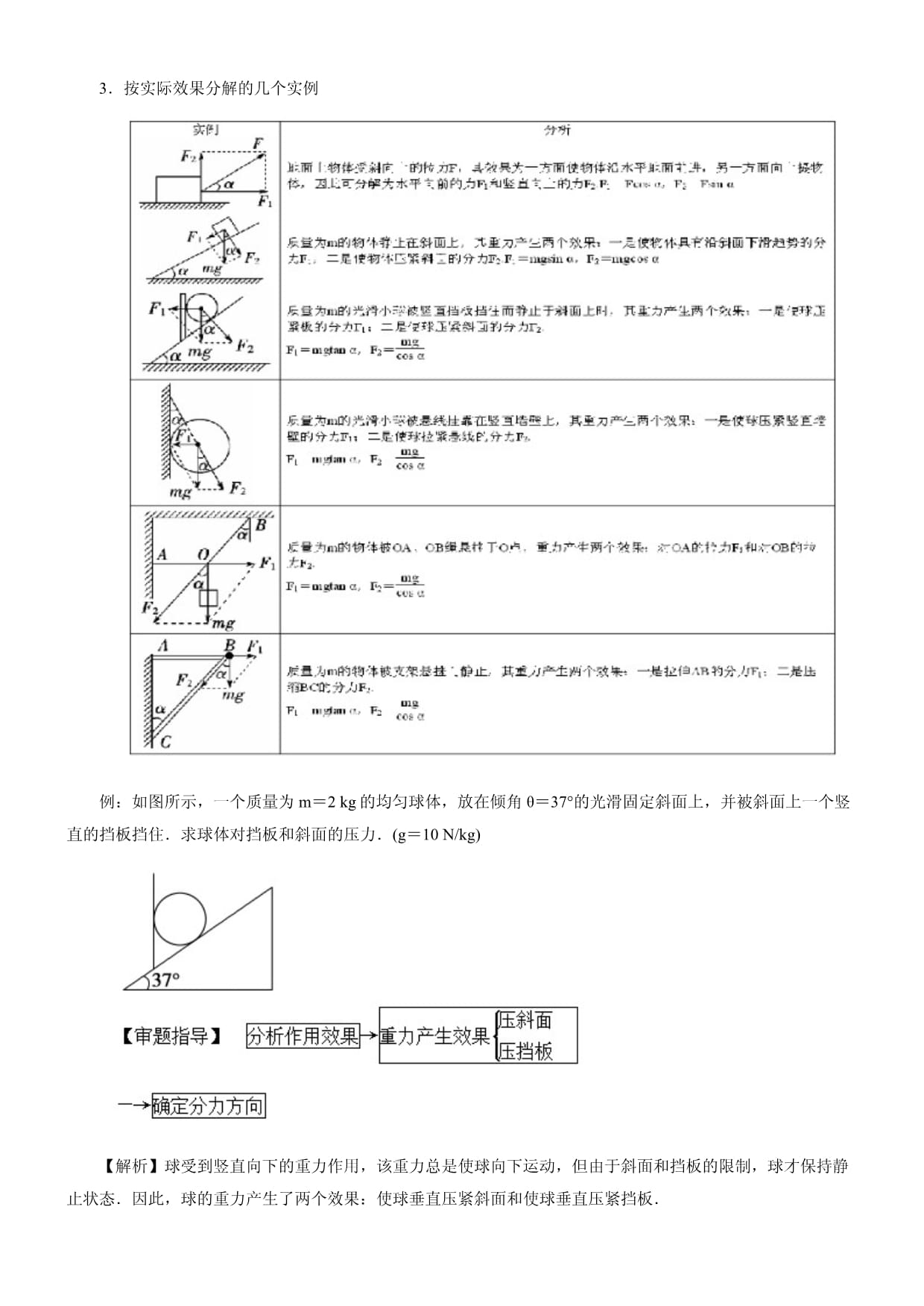
教学过程1.基本知识(1)力的分解：已知一个力求它的分力的过程．(2)分解法则：力的分解是力的合成的逆运算，同样遵循平行四边形定则．(3)分解依据：通常依据力的作用效果进行分解．2．思考判断(1)将一个力F分解为两个力F1和F2，那么物体同时受到F1、F2和F三个力的作用．(×)(2)某个分力的大小可能大于合力．(√)(3)一个力只能分解为一组分力．(×)探究交流为了行车方便和安全，高大的桥往往有很长的引桥，在引桥上，汽车重力有什么作用效果？从力的分解的角度分析，引桥很长有什么好处？【提示】汽车重力的两个作用效果是垂直桥面向下使汽车压斜面和沿桥面向下使汽车下滑或阻碍汽车上行．高大的桥建造很长的引桥可以减小斜面的倾角，即减小汽车重力沿斜面向下的分力，使行车更安全.二、矢量相加的法则1.基本知识(1)矢量：既有大小，又有方向，合成时遵守平行四边形定则或三角形定则的物理量．(2)标量：只有大小，没有方向，求和时按照算术法则相加的物理量.(3)三角形定则：把两个矢量首尾相接，组成三角形，其第三边就是合矢量．2．思考判断(1)矢量、标量的运算方法不同．(√)(2)两个矢量相加的结果可能等于零．(√)(3)两个标量相加的结果可能小于其中的一个量．(√)探究交流既有大小，又有方向的物理量一定是矢量吗？【提示】不一定，一方面既有大小，又有方向，另一方面还需相加时遵从平行四边形定则的物理量才是矢量．三、力的效果分解法【问题导思】1．将一个已知力分解，是否得出唯一的一组分力吗？2．将一个力按实际效果分解时，如何确定分力的方向？3．能否举出一些按实际效果分解的实例？1．一个力在不受条件限制下可分解为无数组分力将某个力进行分解，如果没有条件约束，从理论上讲有无数组解，因为同一条对角线可以构成的平行四边形有无穷多个(如图所示)，这样分解是没有实际意义的．实际分解时，一个力按力的作用效果可分解为两个确定的分力．3．按实际效果分解的几个实例例：如图所示，一个质量为m＝2

kg的均匀球体，放在倾角θ＝37°的光滑固定斜面上，并被斜面上一个竖直的挡板挡住．求球体对挡板和斜面的压力．(g＝10

N/kg)【解析】球受到竖直向下的重力作用，该重力总是使球向下运动，但由于斜面和挡板的限制，球才保持静止状态．因此，球的重力产生了两个效果：使球垂直压紧斜面和使球垂直压紧挡板．如图所示，将球的重力G分解为垂直于斜面的分力F1和垂直于挡板的分力F2，则【答案】对挡板压力大小为15

N，方向向左；对斜面压力大小为25

N，方向垂直斜面向下一个力按力的作用效果可分解为两个确定的分力，分解思路为：1．确定要分解的力．2．按实际作用效果确定两分力的方向．3．沿两分力方向作平行四边形．4．根据数学知识求分力．四、力的正交分解法【问题导思】1．正交分解时，坐标轴的方向是不是力的实际作用效果的方向？2．什么情况下适合应用正交分解法，什么情况下适合应用按效果分解法？3．正交分解过程中，常用到的数学知识有哪些？1．概念将力沿着两个选定的相互垂直的方向分解，叫力的正交分解．2．优点正交分解法是在平行四边形定则的基础上发展起来的，其目的是将矢量运算转化为代数运算．其优点有：(1)可借助数学中的直角坐标系对力进行描述．(2)分解时只需熟知三角函数关系、几何关系，简便、容易求解．3．适用情况常用于三个或三个以上的力的合成．4．步骤(1)建立坐标系：以共点力的作用点为坐标原点，直角坐标系x轴和y轴的选择应使尽量多的力在坐标轴上．(2)正交分解各力：将每一个不在坐标轴上的力分解到x轴和y轴上，并求出各分力的大小，如图所示．正交分解法不一定按力的实际效果分解，而是根据需要在两个相互垂直方向上分解，它是处理力的合成和分解的复杂问题的一种简便方法．例：在同一平面内共点的四个力F1、F2、F3、F4的大小依次为19N、40N、30N和15N，方向如图所示，求它们的合力．【审题指导】解答该题可按以下流程：即合力的大小约为

N，方向与F1夹角为45°，斜向右上方．【答案】合力大小为

N，方向与F1夹角为45°，斜向右上方坐标轴方向的选取技巧应用正交分解法时，常按以下习惯建立坐标轴：1．研究水平面上的物体时，通常沿水平方向和竖直方向选取坐标轴．2．研究斜面上的物体时，通常沿斜面方向和垂直斜面方向选取坐标轴．3．研究物体在杆或绳的作用下转动时，通常沿杆(绳)和垂直于杆(绳)的方向选取坐标轴．五、图解法分析例：绳AO、BO悬挂一个重物，BO水平，O为半圆形支架的圆心，悬点A和B在支架上．悬点A固定不动，将悬点B从图所示位置逐渐移动到C点的过程中，分析绳OA和绳OB上的拉力的大小变化情况．【规范解答】(1)平行四边形法：在支架上选取三个点B1、B2、B3，当悬点B分别移动到B1、B2、B3各点时，AO、BO上的拉力分别为TA1、TA2、TA3和TB1、TB2、TB3，如图所示，从图中可以直观地看出，TA逐渐变小，且方向不变；而TB先变小，后变大，且方向不断改变；当TB与TA垂直时，TB最小．(2)矢量三角形法：将O点所受三力首尾连接，构造出矢量三角形如图所示：将悬点B从图中所示位置逐渐移动到C点的过程中，绳OB上的拉力F3与水平方向的夹角α逐渐增大，根据矢量三角形图可知绳OA的拉力F2逐渐减小，绳OB上的拉力F3先减小后增大．【答案】绳OA的拉力逐渐减小绳OB的拉力先减小后增大．图解法分析力的动态问题的思路1．确定研究对象，作出受力分析图．2．明确各力的特点，哪个力不变，哪个力变化．3．将力的示意图，构造出矢量三角形；或将某力根据其效果进行分解，画出平行四边形．4．根据已知量的变化情况，确定有向线段(表示力)的长度变化，从而判断各个力的变化情况．

课堂小结

板书