初中数学人教九年级上册第二十四章 圆圆周角 PPT

回顾：

在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．圆周角定理·CDABO老师提示:

圆周角定理是承上启下的知识点,要予以重视.

推论：半圆（或直径）所对的圆周角是直角，900的圆周角所对的弦是直径。AOBC1C2C3∵AB是直径∴∠AC1B=900∵∠AC1B=900∴AB是直径

判断命题的真假：

在同圆或等圆中，同弦或等弦所对的圆周角相等。ACBED假命题

同圆或等圆中，同弦或等弦所对的圆周角有什么关系呢？相等或互补

同圆或等圆中，同弦或等弦所对的圆周角相等或互补。新课讲解：

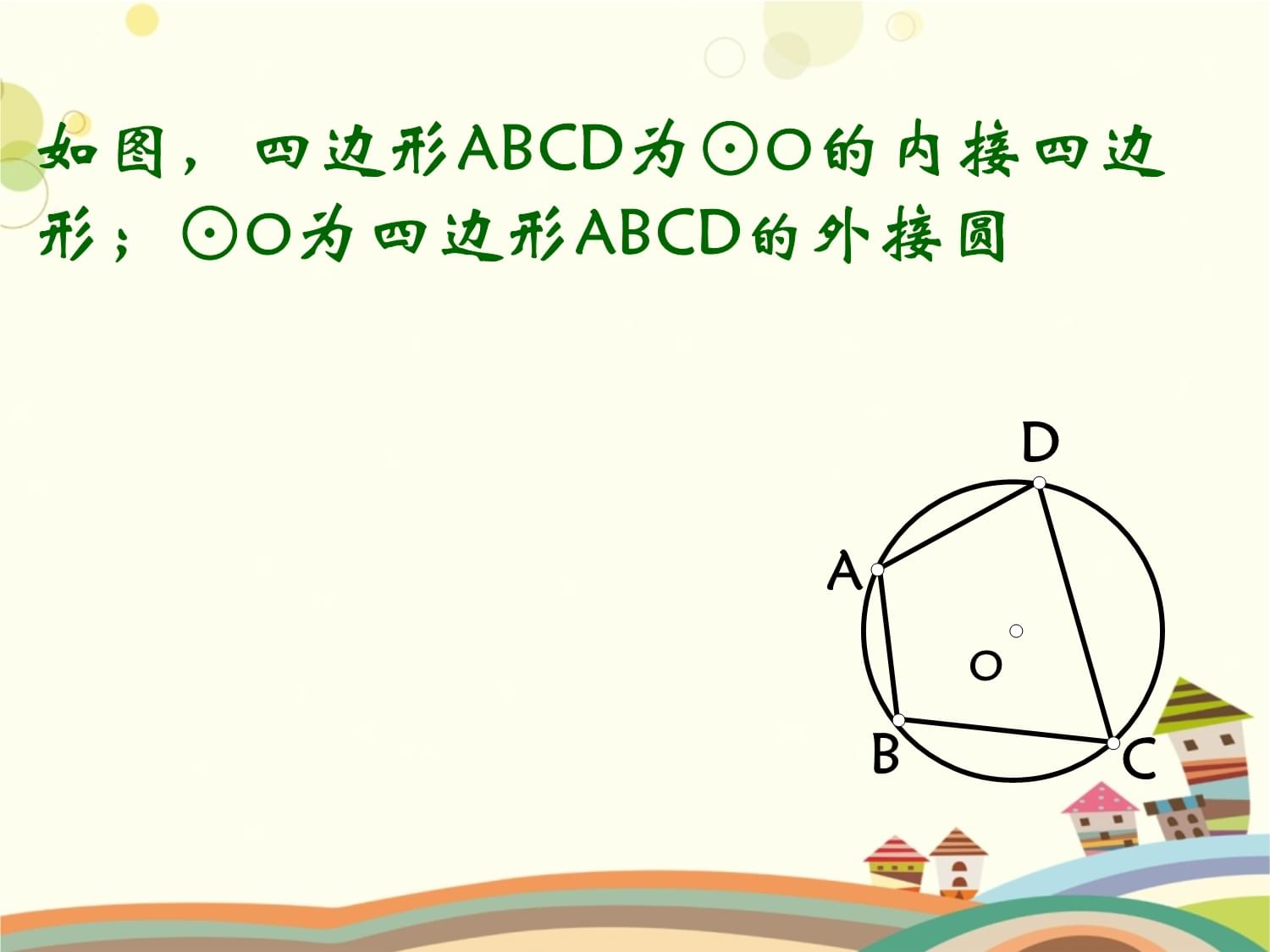
若一个多边形各顶点都在同一个圆上，那么，这个多边形叫做圆内接多边形，这个圆叫做这个多边形的外接圆OBCDEFAOACDEBOCABD如图，四边形ABCD为⊙O的内接四边形；⊙O为四边形ABCD的外接圆CODBA如图：圆内接四边形ABCD中，∵弧BCD和弧BAD所对的圆心角的和是周角∴∠A＋∠C＝180°

同理∠B＋∠D＝180°圆的内接四边形的对角互补。ABCDO圆内接四边形性质定理：圆内接四边形的对角互补，并且一个外角等于它的内对角。E

(1)四边形ABCD内接于⊙O，则∠A+∠C=__

，∠B+∠ADC=_____;若∠B=800，

则∠ADC=______∠CDE=______

(2)四边形ABCD内接于⊙O，∠AOC=1000

则∠B=______∠D=______

(3)四边形ABCD内接于⊙O,∠A:∠C=1:3,则∠A=_____,

180°

180°

100°80°

50°

130°

45°

填空若四边形ABCD为圆内接四边形，则下列哪个选项可能成立（）（A）∠A∶∠B∶∠C∶∠D＝1∶2∶3∶4（B）∠A∶∠B∶∠C∶∠D＝2∶1∶3∶4（C）∠A∶∠B∶∠C∶∠D＝3∶2∶1∶4（D）∠A∶∠B∶∠C∶∠D＝4∶3∶2∶1B例1已知：如图，在△ABC中，AB=AC,以AB为直径的圆交BC于D,交AC于E,(1)BD与CD的大小有什么关系?为什么?(2)求证：⌒

⌒BD=DE

连结AD.∵AB是圆的直径，点D在圆上，∴∠ADB=90°，∴AD⊥BC，∵AB=AC，∴BD=CD,∴⌒⌒BD=DE（同圆或等圆中相等的圆周角所对弧相等）。ABCDE解:BD=CD.理由是:∵AD平分顶角∠BAC，即∠BAD=∠CAD，(2)例2.如图,△ABC的顶点均在⊙O上,AB=4,∠C=30°,求⊙O的直径.

●OACBE

例3.如图⊙O中,D、E分别是AB和AC的中点,DE分别交AB和AC于点M、N;求证:△AMN是等腰三角形.⌒⌒●ODABCNME1、在⊙O中，∠CBD=30°，∠BDC=20°,求∠A。OABDC解法1：∵∠CBD=300，∠BDC=200∴∠C=1800-∠CBD-∠BDC=1300∴∠A=1800-∠C=500（圆内接四边形对角互补）巩固：变式：已知∠OAB等于40度,求∠C的度数.ABCOD3、如图，在⊙O中，AB为直径，CB=CF,弦CG⊥AB，交AB于D，交BF于E。求证：BE=EC））OABDCEGFBE=EC∠EBC=∠ECBCF=BG））CB=BG））CB=CF））AB为直径CG⊥AB4、如图，BC为半圆O的直径，AB=AF,AC与BF交于点M（1）若∠FBC=α，求∠ACB（用α表示）（2）过A作AD⊥BC于D，交BF于E，求证：BE=EM））BCAFDOM5、判断（1）等弧所对的圆周角相等；（）（2）相等的弦所对的圆周角也相等；（）（3）900的角所对的弦是直径；（）（4）同弦所对的圆周角相等。（）求证：如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形·ABCO求证：△ABC

为直角三角形.证明：CO=AB,以AB为直径作⊙O，∵AO=BO， ∴AO=BO=CO.∴点C在⊙O上.又∵AB为直径,∴∠ACB=×180°=90°.已知：△ABC中，CO为AB边上的中线，且CO=AB∴△ABC

为直角三角形.补充：（提示：作出以这条边为直径的圆.）

知识要点（小结）

圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这弧所对的圆心角的一半.

推论1:在同圆或等圆中，相等的圆周角所对的弧相等

推论2：

半圆（或直径）所对的圆周角是直角;90°的圆周角所对的弦是直径．直角三角形的判定：如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形

圆内接四边形的性质：

圆内接四边形对角互补,并且一个外角等于它的内对角拓展：1.如图AB是⊙O的直径，M是劣弧AC的中点，弦AC与BM相交于点D，∠ABC=2∠A，求证：AD=2DC。2、如图所示，AB，AC是⊙O的弦，AD⊥BC于D，交⊙O于F，AE为⊙O的直径，试问两弦BE与CF的大小有何关系，说明理由．

3.已知：如图7-82，AB是⊙O的直径，弦CD⊥AB于E，M为AC上一点，AM的延长线交DC的延长线于F，求证：∠AMD=∠FMC⌒提示：连结BC或连结AD均可。思维拓展变一变：当点D在圆内时，比较∠BAC与∠BDC的大小？CABOD.E小结:圆外角＜圆周角＜圆内角已知⊙O的半径OA=1，弦AB、AC的长分别是、则∠BAC的度数是______________。750OCBANMAOCBMN分类讨论：（注意）150已知圆内接△ABC中,AB=AC,圆心O到BC距离为3cm,圆半径为7cm,则腰长AB=_______,__________。ABCHOABCOH分类讨论：（注意）课前练习：1.

如图，等边三角形ABC，点D是⊙O上一点，则∠BDC=

；60°2.如图，在⊙O中，AB是⊙O的直径，∠D＝20°，则∠AOC的度数为_____

140°ABDCO3.如图，AB和CD都是⊙0的直径，∠AOC=60°，则∠C的度数是

。30°

5.如图,∠C是