统计学课件-22概率分布

宋曼殳首都医科大学公共卫生学院流行病与卫生统计学系概率分布医学科研中的统计学方法概率分布

（probabilitydistribution）概率分布：描述随机变量值xi及这些值对应概率P(X=xi)的表格、公式或图形连续型随机变量概率分布

正态分布离散型随机变量概率分布

二项分布

Poisson分布

随机变量及其概率分布概述连续型随机变量（continousrandomvariable）数据间无缝隙，其取值充满整个区间，无法一一列举每一可能值例如:身高、体重、血清胆固醇含量离散型随机变量（discreterandomvariable）数据间有缝隙，其取值可以列举例如：抛硬币10次，正面的可能取值x为0、1、2、

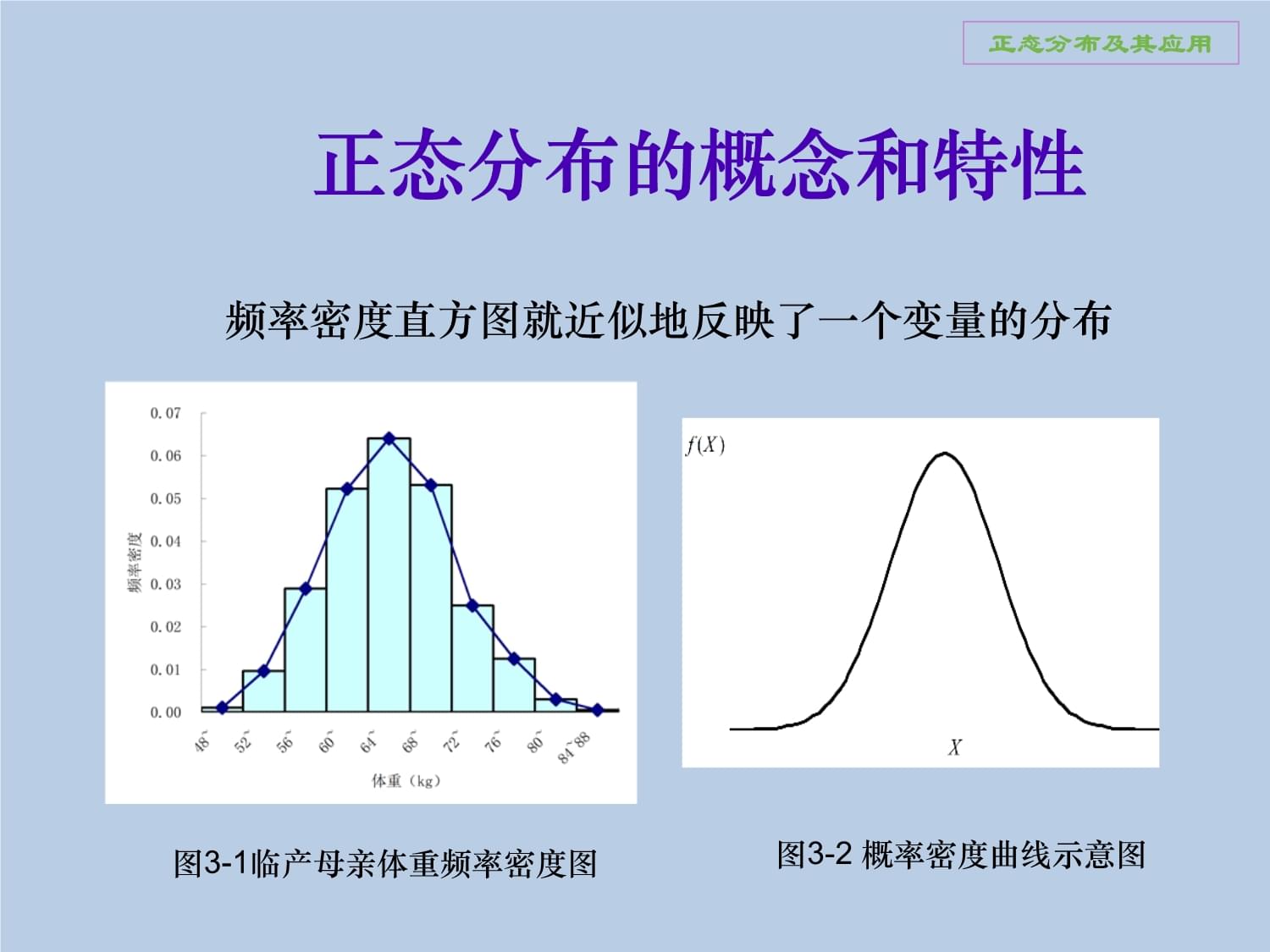
3、4、5、6、7、8、9、10一、正态分布正态分布概念、特征正态曲线下的面积分布规律标准正态分布正态分布的应用估计频数分布制定医学参考值范围质量控制统计方法的理论基础概率分布正态分布的概念和特性正态分布及其应用图3-1临产母亲体重频率密度图图3-2概率密度曲线示意图频率密度直方图就近似地反映了一个变量的分布

当样本量n越来越大，而组距越来越小时，就得到该连续变量所在总体的概率分布。可以设想，如果观察例数逐渐增多，组段数也不断增多，就会形成一条光滑曲线[图(3)]，称为正态分布曲线。正态分布的概念和特性这条呈中间高、两边低、左右基本对称的“钟形”曲线数学上称为正态分布曲线由于纵坐标相当于概率密度，故叫做正态分布的概率密度曲线正态分布及其应用图3-2概率密度曲线示意图正态分布曲线略呈钟形，中间高，两头低，以均数μ为中心，左右对称，均数处最高正态分布的曲线在横轴上方，向两侧逐渐减低，两侧都以横轴为其渐近线正态分布有两个参数，即①均数μ和②标准差σ正态分布的特性正态分布及其应用把服从正态分布的变量表示为：

X~N(μ,σ2)

正态分布的特性

正态分布曲线的参数的意义—①均数μ（位置参数）表示正态分布曲线峰（集中趋势）的位置σ固定时，μ增大，曲线沿横轴向右移动

μ减小，曲线沿横轴向左移动正态分布及其应用

正态分布的特性正态分布曲线的参数—②标准差σ（变异度参数）表示正态变量取值的离中程度μ固定时，σ越大，曲线越宽，表示数据越分散

σ越小，曲线越窄，表示数据越集中正态分布及其应用正态分布的概率密度函数正态分布及其应用式中，μ为总体均数；σ为总体标准差；π=3.14159为圆周率；e为自然对数的底(e≈2.71828),X为变量服从正态分布的变量X的概率密度函数f(x)为图1正态分布的概率密度函数与分布函数X取值落在区间（-∞,x）内的累积概率为概率密度曲线下位于（-∞,x）的图形面积，等于其概率密度函数f(x)在-∞到x上的积分，记作

为正态分布的分布函数。其值表示变量X落在区间（-∞,x）内的概率，对应于从-∞到x概率密度曲线下的阴影面积（常称为左侧尾部面积）图1正态分布的概率密度函数与分布函数图1正态分布的概率密度函数与分布函数图2正态分布的概率利用分布函数可以计算正态分布变量取值在任意区间[a,b）的概率为P(a≤X＜b)=F(b)-F(a)(其几何意义如图2中阴影部分所示)。由图可得P(X≥b)=1-P(X＜b）=1-F(b)正态分布曲线下面积的分布规律正态分布及其应用服从正态分布的随机变量在一区间上曲线下的面积与该随机变量在同一区间内取值的概率相等正态曲线与横轴所夹面积为1正态分布曲线下面积的规律正态分布及其应用1）正态曲线与横轴所夹的面积为12）位于（μ-1.64σ,μ+1.64σ）内的面积为0.90，说明正态变量在μ±1.64σ范围内取值的概率为0.9，在该区间以外取值的概率（两侧的阴影面积之和）为0.1，左右两侧各0.053）位于（μ-1.96σ,μ+1.96σ）内的面积为0.95，说明正态变量在μ±1.96σ范围内取值的概率为0.95，在该区间以外取值的概率（两侧的阴影面积之和）为0.05，左右两侧各0.0254）位于（μ-2.58σ,μ+2.58σ）内的面积为0.99，说明正态变量在μ±2.58σ范围内取值的概率为0.99，在该区间以外取值的概率（两侧的阴影面积之和）为0.01，左右两侧各0.005正态分布曲线下面积分布规律示意图正态分布曲线下的面积分布规律正态分布曲线下的面积分布规律正态分布及其应用正态分布下的概率计算方法一:利用统计软件计算方法二:转化为标准正态分布查表计算曲线下面积的求法：定积分法和标准正态分布法标准正态分布当参数μ和σ已知时，依据正态分布N（μ，σ2）的分布函数公式，正态变量取值落在各区间的概率

[都归结为正态分布曲线下的面积，只需知道分布函数F(x)在区间端点处的函数值]就可以算出，但要通过该公式计算F(x)是困难的实际应用中，要把服从一般正态分布N（μ，σ2）的随机变量X作如下标准化变换：变换后新的随机变量z服从，μ=0，σ=1的正态分布，即Z~N(0，1)正态分布及其应用标准正态分布指数据经标准化变换后，μ=0，σ=1时的正态分布标准正态分布（又称Z分布）:Z~N(0，1)公式任何一个正态分布，都可以通过变换，成为标准正态分布正态分布及其应用mm+sm-sX~N(m,s2)01-1X-msZ=~N(0,1)正态分布及其应用标准正态分布图中阴影部分的面积[表示标准正态变量Z落在（-∞,z）内的概率]即为分布函数的值标准正态分布的概率密度曲线与分布函数示意图z0z10z21-正态分布及其应用标准正态分布图中阴影部分的面积[表示标准正态变量Z落在（-∞,z）内的概率]即为分布函数的值标准正态分布的概率密度曲线与分布函数示意图正态分布的应用1、估计频数分布标准正态分布正态分布及其应用查标准正态分布表（附表C1）得标准正态变量z落在（-∞,z）内的概率值z.00.01.02.03.04.05.06.07.08.09-3.0.0013.0013.0013.0012.0012.0011.0011.0011.0010.0010-2.9.0019.0018.0018.0017.0016.0016.0015.0015.0014.0014-2.8.0026.0025.0024.0023.0023.0022.0021.0021.0020.0019-2.7.0035.0034.0033.0032.0031.0030.0029.0028.0027.0026-2.6.0047.0045.0144.0043.0041.0040.0039.0038.0037.0036-2.5.0062.0060.0059.0057.0055.0054.0052.0051.0049.0048-2.4.0082.0080.0078.0075.0073.0071.0069.0068.0066.0064-2.3.0107.0104.0102.0099.0096.0094.0091.0089.0087.0084-2.2.0139.0136.0132.0129.0125.0122.0119.0116.0113.0110-2.1.0179.0174.0170.0166.0162.0158.0154.0150.0146.0143-2.0.0228.0222.0217.0212.0207.0202.0197.0192.0188.0183-1.9.0287.0281.0274.0268.0262.0256.0250.0244.0239.0233-1.8.0359.0351.0344.0336.0329.0322.0314.0307.0301.0294-1.7.0446.0436.0427.0418.0409.0401.0392.0384.0375.0367-1.6.0548.0537.0526.0516.0505.0495.0485.0475.0465.0455-1.5.0668.0655.0643.0630.0618.0606.0594.0582.0571.0559-1.4.0808.0793.0778.0764.0749.0735.0721.0798.0694.0681表C1标准正态分布(z-分布)密度曲线下的面积[Φ(z)值]自-∞到-z的面积Φ(-∞,-z)，Φ(z,+∞)=1-Φ(-∞,-z)正态分布曲线下面积分布规律示意图正态分布曲线下的面积分布规律-1.4.0808.0793.0778.0764.0749.0735.0721.0798.0694.0681-1.3.0968.0951.0934.0918.0901.0885.0869.0853.0838.0823-1.2.1151.1131.1112.1093.1075.1056.1038.1020.1003.0985-1.1.1357.1335.1314.1292.1271.1251.1230.1210.1190.1170-1.0.1587.1562.1539.1515.1492.1469.1446.1423.1401.1379-0.9.1841.1814.1788.1762.1736.1711.1685.1660.1635.1611-0.8.2119.2090.2061.2033.2005.1977.1949.1922.1894.1867-0.7.2420.2339.2358.2327.2296.2266.2236.2206.2177.2148-0.6.2743.2709.2676.3643.2611.2578.2546.2514.2483.2451-0.5.3085.3050.3015.2981.2946.2912.2877.2843.2810.2776-0.4.3446.3409.3372.3336.3300.3264.3228.3192.3156.3121-0.3.3821.3783.3745.3707.3669.3632.3594.3557.3520.3483-0.2.4207.4168.4129.4090.4052.4013.3974.3936.3897.3859-0.1.4602.4562.4522.4483.4443.4404.4364.4325.4286.4247-0.0.5000.4960.4920.4880.4840.4801.4761.4721.4681.4641z.00.01.02.03.04.05.06.07.08.09正态分布的应用1、估计频数分布例：140名成年男子红细胞均数和标准差分别为4.78×1012/L和0.37×1012/L，求红细胞数在4×1012/L~5.3×1012/L范围内所占的比例?正态分布及其应用z0z10z2正态分布的应用练习：假定一组男孩的体重呈正态分布，体重均数＝40kg、体重的标准差＝4kg，请回答以下问题：（1）体重低于46.6kg的男孩占百分之几？（2）体重大于什么值的男孩占10%？

正态分布及其应用

以z1＝﹣1.65查表，得Φ(z1)＝0.0495≈0.05Φ(z2)＝1－0.05＝0.95

即体重低于46.6kg的男孩占95%z10z24046.6？%

z10z24010%X？（2）以Φ(z)＝10%＝0.10先查表，得z1＝﹣1.28

∵︱z2︱

＝︱z1︱∴z2＝1.28

X＝X+zαSX＝40＋1.28×4＝45.12（kg）

即体重大于45.12kg的男孩占10%2、制定医学参考值范围医学参考值，又称正常值范围，医学上包括绝大多数正常人的某指标值的波动范围确定范围：一般以95%参考值范围最常用按资料特点选取不同方法计算正常值范围的上下限正态分布的应用正态分布及其应用

单侧下限---过低异常单侧下限异常正常单侧上限异常正常异常正常双侧下限双侧上限异常单侧上限---过高异常双侧---过高、过低均异常根据指标含义决定单、双侧范围正态分布的应用2、制定医学参考值范围依据资料的分布类型有以下两种的常用方法：1）正态近似法适用于服从正态分布或近似正态分布的资料双侧参考值范围单侧参考值范围或正态分布的应用2、制定医学参考值范围依据资料的分布类型有以下两种的常用方法：1）正态近似法对于正态分布或近似正态分布的资料，只要样本含量足够大（n＞100）时，可用：作为95%的正常值范围（双侧）正态分布及其应用例:估计例3-4中该地正常成年女子的血清总蛋白

（g/L，g/L）的95%参考值范围。解：由于该地正常成年女子血清总蛋白近似服从正态分布，可用正态分布法计算。因血清总蛋白过多或过少均属异常，所以应取双侧，即计算95%参考值范围的上下限。下限为：

（g/L）上限为：

（g/L）故该地正常成年女子血清总蛋白的95%参考值范围为65.35~80.25(g/L)。正态分布的应用正态分布及其应用正态分布的应用2、制定医学参考值范围2）百分位数法适用于偏态分布资料、分布型未知的资料以及分布末端有不确定值的资料双侧95%参考值范围单侧95%参考值范围正态分布及其应用或正态分布的应用例：某地调查110名健康成年男子的第一秒肺通气量（近似服从正态分布）得：均数为4.2（L）标准差为0.7（L）请据此估计该地成年男子第一秒肺通气量的95%正常值范围？正态分布及其应用正态分布的应用因第一秒肺通气量仅过低属异常，故此正常值范围属仅有下限的单侧正常值范围又因此资料近似正态分布，故可用正态分布法即该地成年男子第一秒肺通气量的95%正常值范围不低于3.05(L)

正态分布及其应用

例

测得某年某地名正常人的尿汞值如下表，试制定正常人尿汞值的95%参考值范围。

表

282名正常人尿汞值（）测量结果单侧上限常用参考值范围的制定

参考值范围（%）正态分布法百分位数法双侧单侧双侧单侧下限上限下限上限90P5~P95P10P9095P2.5~P97.5P5P9599P0.5~P99.5P1P99正态分布的应用3、质量控制绘出质量控制图正态分布及其应用上、下警戒限上、下控制限各测定值均在警戒限以内，且随机地分布在中心线的两侧，说明质量在控制中正态分布的应用3、质量控制例如，某实验室对同一控制血清作尿酸定量测定，连续观察20天，得20个数据如下（mg/dl）：正态分布及其应用5.05.05.04.84.65.14.85.04.84.84.85.04.64.74.74.64.75.14.74.7正态分布的应用4、统计方法的理论基础许多统计方法（如t检验、方差分析等）都要求指标服从正态分布有些统计量的分布（如t

分布等）都是在正态分布的基础上推演出来的正态分布在统计学中占有极其重要的地位正态分布及其应用1、正态分布是一种很重要的连续型分布，很多医学现象服从正态分布或近似正态分布，或经变量转换转换为正态分布，可按正态分布规律来处理，是许多统计学方法的理论基础2、正态分布的特征：①曲线在横轴上方，均数处最高；②以均数为中心，左右对称；③确定正态分布的两个参数是均数与标准差3、正态曲线下面积的分布有一定规律。利用此规律可用于估计医学参考值范围和质量控制小结正态性转换的常见方法

1.对数变换:适用于(1)对数正态分布资料,如抗体滴度,疾病潜伏期等;(2)样本标准差与均数成比例

2.平方根变换:适用于(1)服从泊松分布资料,如一些发病率较低的疾病(2)轻度的偏态分布的资料

3.平方根反正弦变换:适用于率或百分比资料,如患病率等

4.倒数变换:适用于数据两端波动较大的数据

练习：某年某地不同年龄组男童身高资料如下：

年龄组人数均数（cm）标准差cm）1～2月

10056.32.15～6月

12066.52.23～3.5岁30096.13.15～5.5岁

400107.83.3

（1）上述资料是否表明6岁以下男童的平均身高和身高的变异程度均随年龄增长而增加？（2）若身高服从正态分布，试估计上述300名3～3.5

岁男童中身高在95.0～100cm范围内者有多少人？（3）计算5～5.5岁年龄组男童身高的正常值范围？

例题为估计某地居民尿汞值的参考值范围，测得某地200名正常成人的尿汞值如下表，试根据该样本资料估计该地居民尿汞值的95%正常值范围。尿汞值0～4～8～12～16～20～24～28～32～36～40～44～48～例数45304120151213546342某地200名正常成人的尿汞值/

习题解法一：计算得该样本资料的均数13.78（），标准差11.71（），于是估计该地居民尿汞值的95%正常值范围为（，）=（-9.17，36.73）。解法二：估计该地居民尿汞值的95%正常值范围为（，）=（2.66,24.90）。

习题正确否？案例辨析以上解法均是错误的。上述解法均利用正态分布法估计正常值范围，但却忽略了对该资料的正态性判断或检验。正确做法严格的正态性检验常用的方法有Z检验（通常称为矩法）、W

检验、D检验等，需要借助统计软件完成。在这里我们用粗略判断的方法：作出频率分布图看是否对称，如果对称可初步判断为正态分布，否则判为非正态。该例频率分布明显不对称习题由此图可粗略判断尿汞值这个指标不服从正态分布（经对数变换后频率分布仍不对称），所以不能用正态分布法估计正常值范围，而应用适合描述偏态分布的百分位数法，计算，故估计该地居民尿汞值的95%正常值范围不高于38（）。习题在本例中，如果该地居民尿汞值呈正态分布，则有估计该地居民尿汞值的95%正常值范围为（0，）=（0，32.98）（）因为汞是对人身体有害的微量元素，越少越好，又不可能取负值，下限应该为0，只需求出单侧上限即可。习题三、计算题:调查某市2000年110名20岁男性青年的身高（cm）资料如下：

173.1166.8172.9175.9172.8170.5174.1174.2175.7173.5168.2173.7184.4174.8172.5174.9174.9174.2173.8176.2170.9165.0176.3174.2179.8174.5180.5171.5178.9171.5166.7170.8168.8177.5174.5183.5182.0170.9173.5177.5181.2177.1172.3176.5174.0174.3174.6172.6171.3173.1176.9170.5174.2177.5176.6182.3172.1169.9179.5175.8178.6180.6175.6173.3168.7174.5178.5171.3172.0173.2168.8176.0182.6169.5177.5180.6181.5175.1165.2168.0175.4169.2170.0171.9176.6178.8177.2173.4168.5177.6175.8164.8175.6180.0176.6176.5177.7174.1180.8170.6173.8180.7176.3177.5178.3176.0174.8180.8176.5179.2

（1）试估计当年该市20岁男性青年中，身高在175.0~178.0（cm）内的占多大比例？（2）估计当年该市95%以及99%的20岁男青年身高范围。（3）若当年由该市随机抽查1名20岁男青年，试估计其身高超过180cm的概率。