【其中考试】2020-2021湖北省某校初二（上）期中考试数学试卷

试卷第=page2626页，总=sectionpages2727页试卷第=page2727页，总=sectionpages2727页2020-2021湖北省某校初二（上）期中考试数学试卷一、选择题

1.如图所示，图中不是轴对称图形的是(

)A. B. C. D.

2.有4cm和6cmA.1cm B.2cm C.7

3.如图，∠ABC=∠ABD，还应补充一个条件，才能推出△ABC≅△ABD.

补充下列其中一个条件后，不一定能推出A.BC=BD B.AC=AD

C.

4.如果n边形的内角和是它外角和的3倍，则n等于(

)A.6 B.7 C.8 D.9

5.如图，将三角形纸板的直角顶点放在直尺的一边上，∠1=20∘，∠2=40∘，则∠3等于A.20∘ B.40∘ C.60

6.如图，AD是△ABC的角平分线，过点D作DE⊥AB于E，DF⊥AC于F，则下列结论①DE=DF；②BD=CD；③A.1个 B.2个 C.3个 D.4个

7.如图，在△ABC中，DE是AC的垂直平分线，且分别交BC，AC于点D和E，∠B=60∘，∠C=A.50∘ B.70∘ C.75∘ D.80

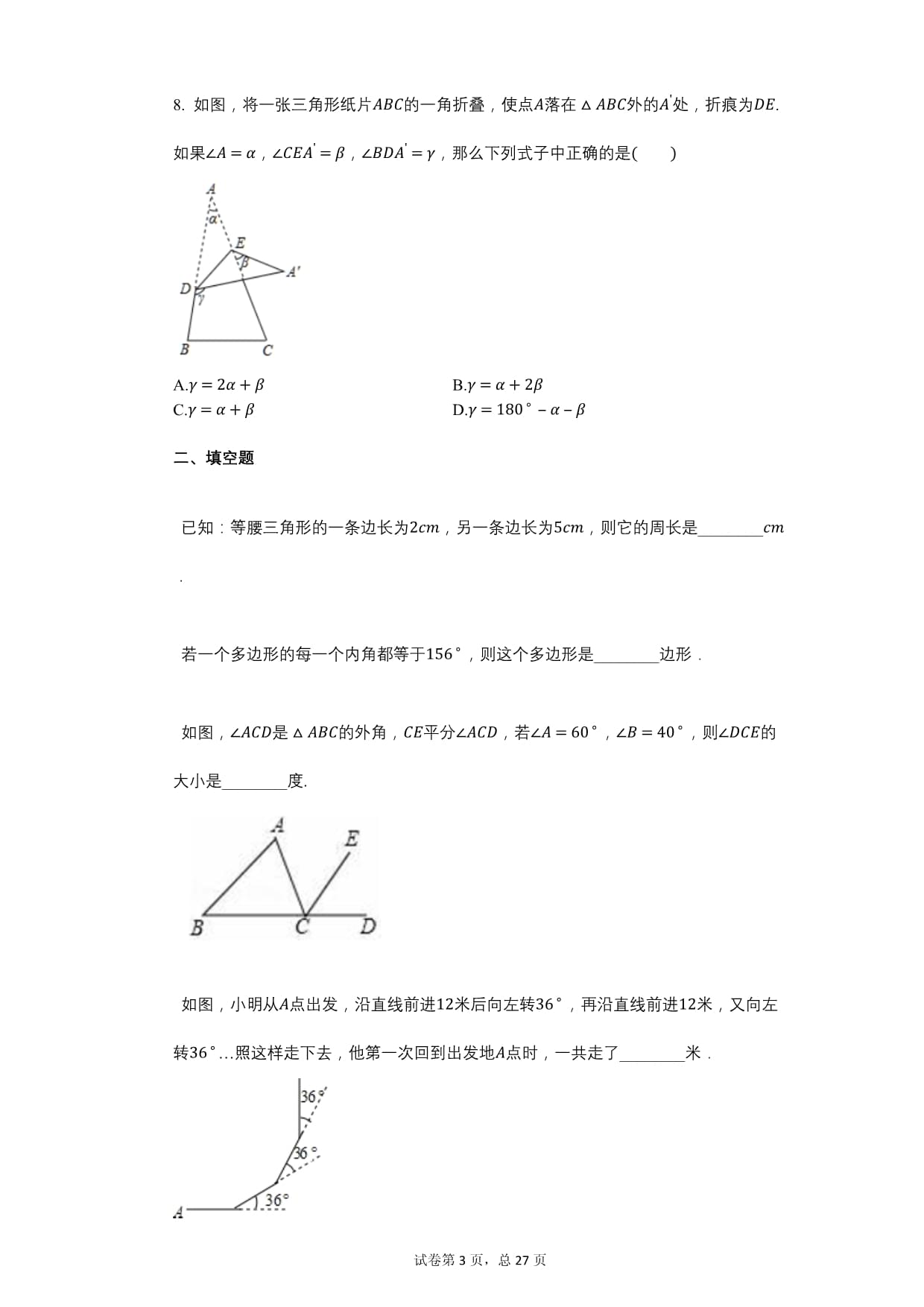
8.如图，将一张三角形纸片ABC的一角折叠，使点A落在△ABC外的A'处，折痕为DE.如果∠A=α，∠CEA'=A.γ=2α+β B.γ=α+2β二、填空题

已知：等腰三角形的一条边长为2cm，另一条边长为5cm，则它的周长是________cm

若一个多边形的每一个内角都等于156∘，则这个多边形是________边形．

如图，∠ACD是△ABC的外角，CE平分∠ACD，若∠A=60∘，∠B=

如图，小明从A点出发，沿直线前进12米后向左转36∘，再沿直线前进12米，又向左转36∘…照这样走下去，他第一次回到出发地A点时，一共走了________米．

如图，△ABC中，AB=AC，AB的垂直平分线交边AB于D点，交边AC于E点，若△ABC与△EBC的周长分别是40cm，24cm

如图，在△ABC中，∠C=46∘，将△ABC沿着直线l折叠，点C落在点D的位置，则

等腰三角形ABC中，∠A=50∘

如图，在△ABC中，AD，CF分别是∠BAC，∠ACB的角平分线，且AD，CF交于点I，IE⊥BC于E，下列结论：①∠BIE=∠CID三、解答题

如图，在△ABC中，BD⊥AC，垂足为D．∠ABD=54∘,∠DBC=

已知：如图，AB=AE，∠1=∠2，∠B=∠E．求证：

如图，在直角坐标系中，先描出点A(1, 3)，点B(4, 1)．

(1)描出点A关于x轴的对称点A1的位置，写出A1的坐标(2)在x轴上找一点C，使AC+(3)用尺规在x轴上找一点P，使PA=

如图，∠ACB=90∘，AC=BC．AD⊥CE，BE⊥CE，垂足分别是点D，E

如图，点D在CB的延长线上，DB=CB，点E在AB上，连接DE，DE=AC，

求证：∠

如图，在直角坐标系中，A，B，C，D各点的坐标分别为(-7, 7)，(-7, 1)，(-3, 1)，(-1, 4)．

(1)在给出的图形中，画出四边形ABCD关于y轴对称的四边形A1(2)写出点A1和C(3)求四边形A1

如图，在正方形ABCD中，AB=BC=CD=AD，∠BAD=∠B=∠C=∠D=90∘，点E，F分别在正方形(1)△ABF与△(2)求∠EAF(3)若AG=4，△AEF的面积是6，求

如图，已知B(-1, 0)，C(1, 0)，A为y轴正半轴上一点，点D为第二象限一动点，E在BD的延长线上，CD交AB于F，且∠BDC=∠(1)求证：∠ABD(2)求证：AD平分∠CDE(3)若在D点运动的过程中，始终有DC=DA+DB，在此过程中，

参考答案与试题解析2020-2021湖北省某校初二（上）期中考试数学试卷一、选择题1.【答案】C【考点】轴对称图形【解析】根据轴对称图形的概念：如果一个图形沿一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形．据此对图中的图形进行判断．【解答】解：A、有四条对称轴，是轴对称图形，故本选项错误；

B、有三条对称轴，是轴对称图形，故本选项错误；

C、不是轴对称图形，因为找不到任何这样的一条直线，

使它沿这条直线折叠后，直线两旁的部分能够重合，

即不满足轴对称图形的定义，故本选项正确；

D、有二条对称轴，是轴对称图形，故本选项错误．

故选C．2.【答案】C【考点】三角形三边关系【解析】根据三角形的三边关系可得6-4<第三根小棒的长度<6+4，再解不等式可得答案．【解答】解：设第三根小棒的长度为xcm，

由题意得：6-4<x<6+4，

解得：2<x<10.3.【答案】B【考点】全等三角形的性质与判定【解析】全等三角形的判定定理有SAS，ASA，AAS，SSS，已知有∠ABC=∠【解答】解：A选项，因为BD=CB，∠ABD=∠ABC，AB=AB，

所以根据SAS能推出△ABC≅△ABD，故本选项不符合题意；

B选项，因为AD=AC，AB=AB，∠ABD=∠ABC，

根据SSA不能推出△ABC≅△ABD，故本选项符合题意；

C选项，因为∠ADB=∠ACB，∠ABD=∠ABC，AB=4.【答案】C【考点】多边形的外角和多边形的内角和【解析】此题暂无解析【解答】解：根据题意列方程，得：

(n-2)⋅180∘=3×360∘，

解得n=8，

5.【答案】A【考点】三角形的外角性质平行线的性质【解析】如图，首先运用平行线的性质求出∠4，然后借助三角形的外角性质求出∠3，即可解决问题．【解答】解：由题意得：∠4=∠2=40∘；

由外角定理得：∠4=∠1+∠3，

∴∠3=∠4-∠1=40∘-206.【答案】C【考点】全等三角形的性质与判定【解析】此题暂无解析【解答】解：∵AD是△ABC的角平分线，

∴∠BAD=∠DAC.

在△ADE和△ADF中，

∠BAD=∠CAD，∠AED=∠AFD，AD=AD，7.【答案】B【考点】三角形内角和定理线段垂直平分线的性质【解析】根据线段垂直平分线的性质得到DA=DC，根据等腰三角形的性质得到∠DAC【解答】解：∵DE是AC的垂直平分线，

∴DA=DC，

∴∠DAC=∠C=25∘，

∵∠B=60∘，8.【答案】A【考点】三角形的外角性质【解析】根据三角形的外角得：∠BDA'【解答】解：由折叠得：∠A=∠A'，

∵∠BDA'=∠A+∠AFD，∠AFD=∠A'+∠二、填空题【答案】12【考点】等腰三角形的判定与性质三角形三边关系【解析】根据已知条件和三角形三边关系可知；等腰三角形的腰长不可能为2cm，只能为5【解答】解：当腰长是2cm时，因为2+2<5，不符合三角形的三边关系，应排除；

当腰长是5cm时，因为2+5>5，符合三角形三边关系，此时周长是12cm．

【答案】十五【考点】多边形内角与外角【解析】先求出多边形一个外角的度数，然后根据多边形的外角和为360∘【解答】解：∵多边形的每一个内角都等于156∘，

∴多边形的每一个外角都等于180∘-156∘=24【答案】50【考点】三角形的外角性质角平分线的定义【解析】根据三角形外角性质求出∠ACD【解答】解：∵∠A=60∘，∠B=40∘，

∴∠ACD=∠A+∠B【答案】120【考点】多边形内角与外角【解析】根据题意多边形的外角和为360∘，由题意得到小明运动的轨迹为正10【解答】解：由题意得：360∘÷36∘=10，

则他第一次回到出发地A点时，一共走了12×10=120【答案】16【考点】等腰三角形的判定与性质线段垂直平分线的性质等腰三角形的性质与判定【解析】首先根据DE是AB的垂直平分线，可得AE=BE；然后根据△ABC的周长=AB+AC+BC，△EBC的周长【解答】解：∵DE是AB的垂直平分线，

∴AE=BE；

∵△ABC的周长=AB+AC+BC，

△EBC的周长=BE+EC+BC

=AE【答案】92【考点】三角形的外角性质翻折变换（折叠问题）【解析】由折叠的性质得到∠D【解答】解：如图：

由折叠的性质得：∠D=∠C=46∘，

根据外角性质得：∠1=∠3+∠C，∠3=∠2+∠D，

则∠1=∠2+∠C+∠【答案】50∘或80∘【考点】等腰三角形的性质【解析】分三种情况分析求解即可.【解答】解：①若∠A=50∘为顶角，

则∠B=180∘-50∘2=65∘；

②若∠B为顶角，

则∠C=∠A=50∘，

∴∠B=180∘-【答案】①③④【考点】角平分线的性质三角形内角和定理全等三角形的性质与判定三角形的内切圆与内心【解析】①由I为△ABC三条角平分线的交点，IE⊥BC于E，得到∠ABI=∠IBD，由于∠CID+∠ABI=90∘，即∠CIE+∠DIE+∠IBD=90∘，由已知条件得到∠IBD+∠BID+∠DIE=90∘，于是得到∠BIE=∠CID；即①成立；②由I是△ABC三内角平分线的交点，得到点I到△ABC三边的距离相等，根据三角形的面积即可得到即②成立；③如图过I作IH⊥AB于H【解答】解：①∠ABC+∠ACB+∠BAC=180∘,

∠IBE=12∠ABC，∠IAC=12∠BAC，∠ICA=12∠ACB，

∠IBE+∠IAC+∠ICA=90∘，

∠CID=∠IAC+∠ICA=90∘-∠IBE=∠BIE.

故①正确；

②只有在

∠ABC=60∘

的条件下，

AC=AF+DC，故②错误；

③如图过I作IH⊥AB于H，IG⊥三、解答题【答案】解：∵在△ABC中，BD⊥AC，∠ABD=54∘，

∴∠BDA=90∘，

∴∠A=∠BDA-∠ABD=90【考点】三角形内角和定理【解析】无【解答】解：∵在△ABC中，BD⊥AC，∠ABD=54∘，

∴∠BDA=90∘，

∴∠A=∠BDA-∠ABD=90【答案】证明：∵∠1=∠2，

∴∠1+∠BAD=∠2+∠BAD，

即：∠EAD=∠BAC，

在△EAD和△BAC【考点】全等三角形的性质【解析】由∠1=∠2可得：∠EAD=∠BAC，再有条件AB=AE，∠B=∠【解答】证明：∵∠1=∠2，

∴∠1+∠BAD=∠2+∠BAD，

即：∠EAD=∠BAC，

在△EAD和△BAC中【答案】(1, -3)(2)如图所示：点C即为所求.(3)如图所示：点P即为所求．

【考点】关于x轴、y轴对称的点的坐标轴对称——最短路线问题【解析】（1）直接利用关于x轴对称点的性质得出答案；

（2）利用轴对称求最短路线作法得出答案；

（3）利用线段垂直平分线的作法得出答案．【解答】解：(1)如图所示：

A1的坐标(1, -3).

故答案为：(1, -3)(2)如图所示：点C即为所求.(3)如图所示：点P即为所求．

【答案】解：∵BE⊥CE，AD⊥CE，

∴∠E=∠ADC=90∘，

∴∠EBC+∠BCE=90∘．

∵∠BCE+∠ACD=90∘，

∴∠EBC=∠DCA【考点】全等三角形的性质与判定【解析】根据条件可以得出∠E＝∠ADC＝90∘，进而得出△CEB≅△ADC，就可以得出【解答】解：∵BE⊥CE，AD⊥CE，

∴∠E=∠ADC=90∘，

∴∠EBC+∠BCE=90∘．

∵∠BCE+∠ACD=90∘，

∴∠EBC=∠DCA．

【答案】证明：延长EB到F点，使得BF=BE，连接CF，

∵BE=BF，∠DBE=∠CBF，BD=BC，

∴△BDE≅△BCFSAS【考点】全等三角形的性质与判定【解析】延长EB到F点，使得BF=BE连接CF．证明△【解答】证明：延长EB到F点，使得BF=BE，连接CF，

∵BE=BF，∠DBE=∠CBF，BD=BC，

∴△BDE≅△BCFSAS【答案】解：(1)如图所示：

.

(2)由图可知，

A1(7, 7)，(3)S【考点】作图-轴对称变换位置的确定坐标与图形性质【解析】（1）根据关于y轴对称的点的坐标特点画出四边形A1（2）根据各点在坐标系中的位置写出点A1和C（3）利用正方形的面积减去C1，D【解答】解：(1)如图所示：

.(2)由图可知，

A1(7, 7)，(3)S【答案】解：(1)结论：△ABF≅△AGF．

理由：在Rt△ABF与Rt△(2)∵△ABF≅△AGF

∴∠BAF=∠GAF，

同理易得：△AGE≅△ADE，

有∠(3)由题易知S△ABF=S△AGF，S△【考点】直角三角形全等的判定正方形的性质三角形的面积【解析】（1）根据HL可得出△ABF（2）只要证明∠BAF=∠GAF，∠（3）设FC=x，EC=y，则BF=4-【解答】解：(1)结论：△ABF≅△AGF．

理由：在Rt△ABF与Rt△(2)∵△ABF≅△AGF

∴∠BAF=∠GAF，

同理