2022-2023年度 名师 《中位线》参考教案_第1页
2022-2023年度 名师 《中位线》参考教案_第2页
2022-2023年度 名师 《中位线》参考教案_第3页
2022-2023年度 名师 《中位线》参考教案_第4页
2022-2023年度 名师 《中位线》参考教案_第5页
已阅读5页，还剩1页未读， 继续免费阅读

下载本文档

版权说明：本文档由用户提供并上传，收益归属内容提供方，若内容存在侵权，请进行举报或认领

文档简介

1、PAGE6中位线教学目标：1经历三角形中位线的性质定理形成过程，掌握这个定理，并能利用它解决简单的问题。2通过命题的教学了解常用的辅助线的作法,并能灵活运用它们解题。3进一步训练说理的能力。4通过学习，进一步培养自主探究和合作交流的学习习惯；进一步了解特殊与一般的辩证唯物主义观点；转化的思想。教学重点：经历三角形中位线的性质定理形成过程，掌握这个定理，并能利用它解决简单的问题。教学难点：进一步训练说理的能力。教学过程：（一）问题导入在中，我们曾解决过如下的问题：如图，ABC中，DEBC，则ADEABC。由此可以进一步推知，当点D是AB的中点时，点E也是AC的中点。现在换一个角度考虑，如果点D、

2、E原来就是AB与AC的中点，那么是否可以推出DEBC呢DE与BC之间存在什么样的数量关系呢（二）探究过程1、猜想从画出的图形看，可以猜想：DEBC，且DEBC2、证明：如图，ABC中，点D、E分别是AB与AC的中点AA，ADEABC（如果一个三角形的两条边与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似），ADEABC，（相似三角形的对应角相等，对应边成比例），DEBC且思考：本题还有其它的解法吗已知：如图所示，在ABC中，ADDB，AEEC。求证：DEBC，DEBC。分析:要证DEBC，DEBC，可延长DE到F，使EFDE，于是本题就转化为证明DFBC，DEBC，故只要证

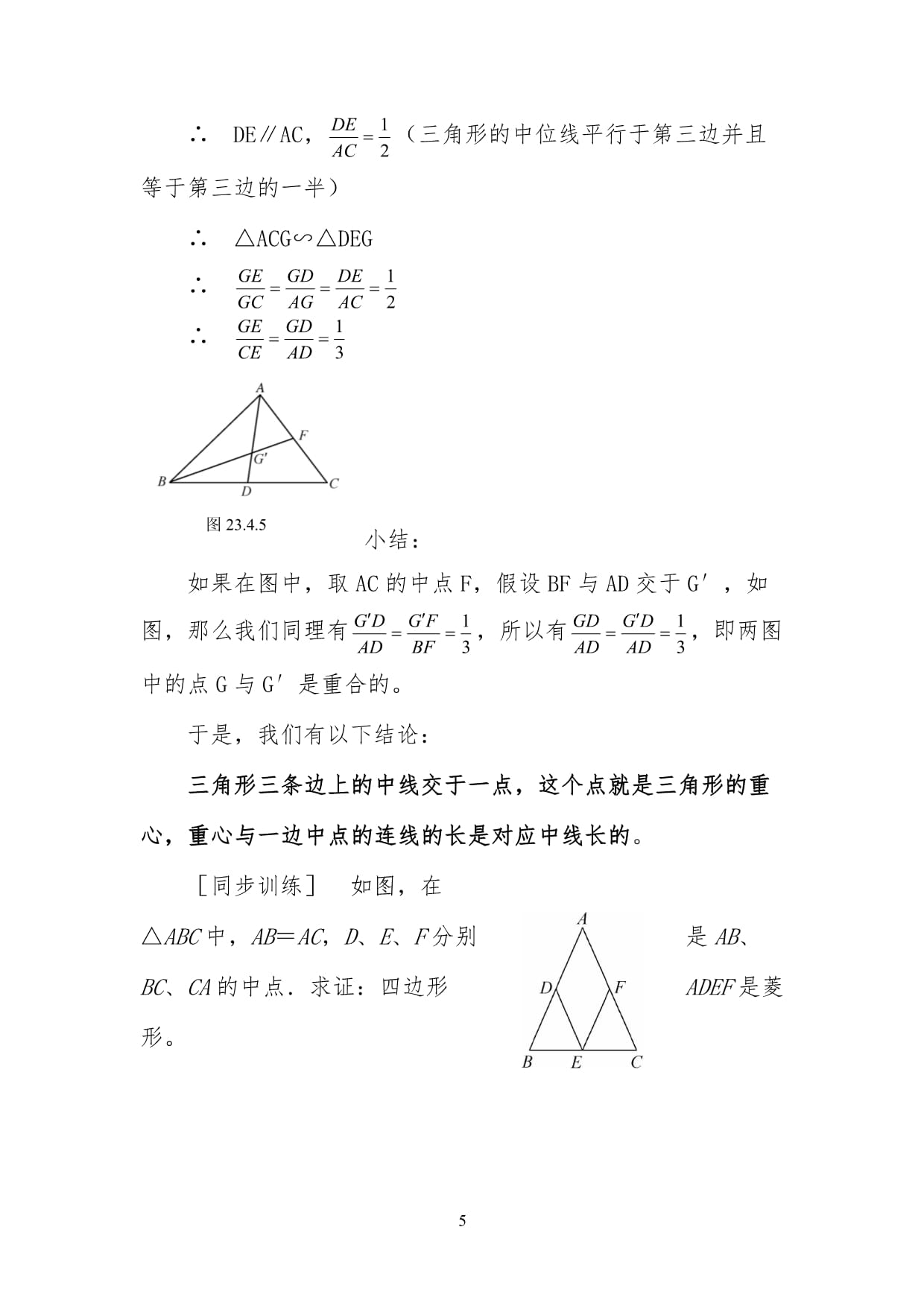
3、明四边形BCFD为平行四边形。还可以作如下的辅助线作法。3、概括我们把连结三角形两边中点的线段叫做三角形的中位线，并且有三角形的中位线平行于第三边并且等于第三边的一半。介绍三角形的中位线时，强调指出它与三角形中线的区别。（三）应用例1求证三角形的一条中位线与第三边上的中线互相平分。已知：如图所示，在ABC中，ADDB，BEEC，AFFC。求证：AE、DF互相平分。证明连结DE、EF因为ADDB，BEEC所以DEAC（三角形的中位线平行于第三边并且等于第三边的一半）同理EFAB所以四边形ADEF是平行四边形因此AE、DF互相平分（平行四边形的对角线互相平分）例2如图，ABC中，D、E分别是边BC、AB的中点，AD、CE相交于G。求证：证明连结EDD、E分别是边BC、AB的中点DEAC，（三角形的中位线平行于第三边并且等于第三边的一半）ACGDEG小结：如果在图中，取AC的中点F，假设BF与AD交于G，如图，那么我们同理有，所以有，即两图中的点G与G是重合的。于是，我们有以下结论：三角形三条边上的中线交于一点，这个点就是三角形的重心，重心与一边中点的连线的长是对应中线长的。同步训练如图，在ABC中，ABAC，D、E、F

人人文库> 全部分类> 教育资料 > 辅导培训

温馨提示

  • 1. 本站所有资源如无特殊说明，都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
  • 2. 本站的文档不包含任何第三方提供的附件图纸等，如果需要附件，请联系上传者。文件的所有权益归上传用户所有。
  • 3. 本站RAR压缩包中若带图纸，网页内容里面会有图纸预览，若没有图纸预览就没有图纸。
  • 4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
  • 5. 人人文库网仅提供信息存储空间，仅对用户上传内容的表现方式做保护处理，对用户上传分享的文档内容本身不做任何修改或编辑，并不能对任何下载内容负责。
  • 6. 下载文件中如有侵权或不适当内容，请与我们联系，我们立即纠正。
  • 7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

最新文档

评论

0/150

提交评论