高考数学压轴专题2020-2021备战高考不等式全集汇编附答案

1、新高考数学不等式练习题一、选择题.已知实数x 0,y 0,则2x 2y 4”是xy 1”的（）A.充要条件B.必要不充分条件C.充分不必要条件D.既不充分也不必要条件【答案】C【解析】【分析】利用基本不等式和充分，必要条件的判断方法判断【详解】Q 2x 2y 2立丁 且 2x 2y 4 ,2y/2rT 4/2 2 x y 2 ,等号成立的条件是x y ,又Q x y 2 xy , x 0, y 0 xy 2 xy 1 ,等号成立的条件是x y ,2x 2y 4 xy 1 ,1反过来，当x 2, y 时，此时xy 1,但2x 2y 4 ,不成立，32x 2y 4”是xy 1”的充分不必要条件.故

2、选:C【点睛】本题考查基本不等式和充分非必要条件的判断，属于基础题型x 3y 6 0,2 .若x, y满足约束条件x y 6 0,则z x y的最小值为（）y 1,4B. 0C. 2D. 4【答案】D【解析】【分析】画出约束条件所表示的平面区域，结合图象确定目标函数的最优解，代入即可求解. 【详解】x 3y 6 0由题意，画出约束条件x y 6 0所表示的可行域，如图所示，y 1目标函数z x y,可化为直线y x z当直线y x z经过a时，z取得最小值,x 3y 6 0又由，解得A( 3,1),y 1所以目标函数的最小值为zmin3 14.故选：D.【点睛】3,关于x的不等式ax b 0的

3、解集是 解集是()A. (, 1)U(3,)C (1,3) 【答案】A 【解析】 【分析】 b 由ax b 0的解集，可知a 0及一 a而可求出 ax b x 30的解集.【详解】由ax b 0的解集为(1, +?)，可知a 令 ax b x 30,解得 x11 ,因为a 0,所以ax b x 30的本题主要考查简单线性规划求解目标函数的最值问题.其中解答中正确画出不等式组表示 的可行域，利用 画、二移、三求”，确定目标函数的最优解是解答的关键，着重考查了 数形结合思想，及推理与计算能力.(1,),则关于x的不等式(ax b)(x 3) 0的( 1,3)D. (,1)U(3,)1 ,进而可求出

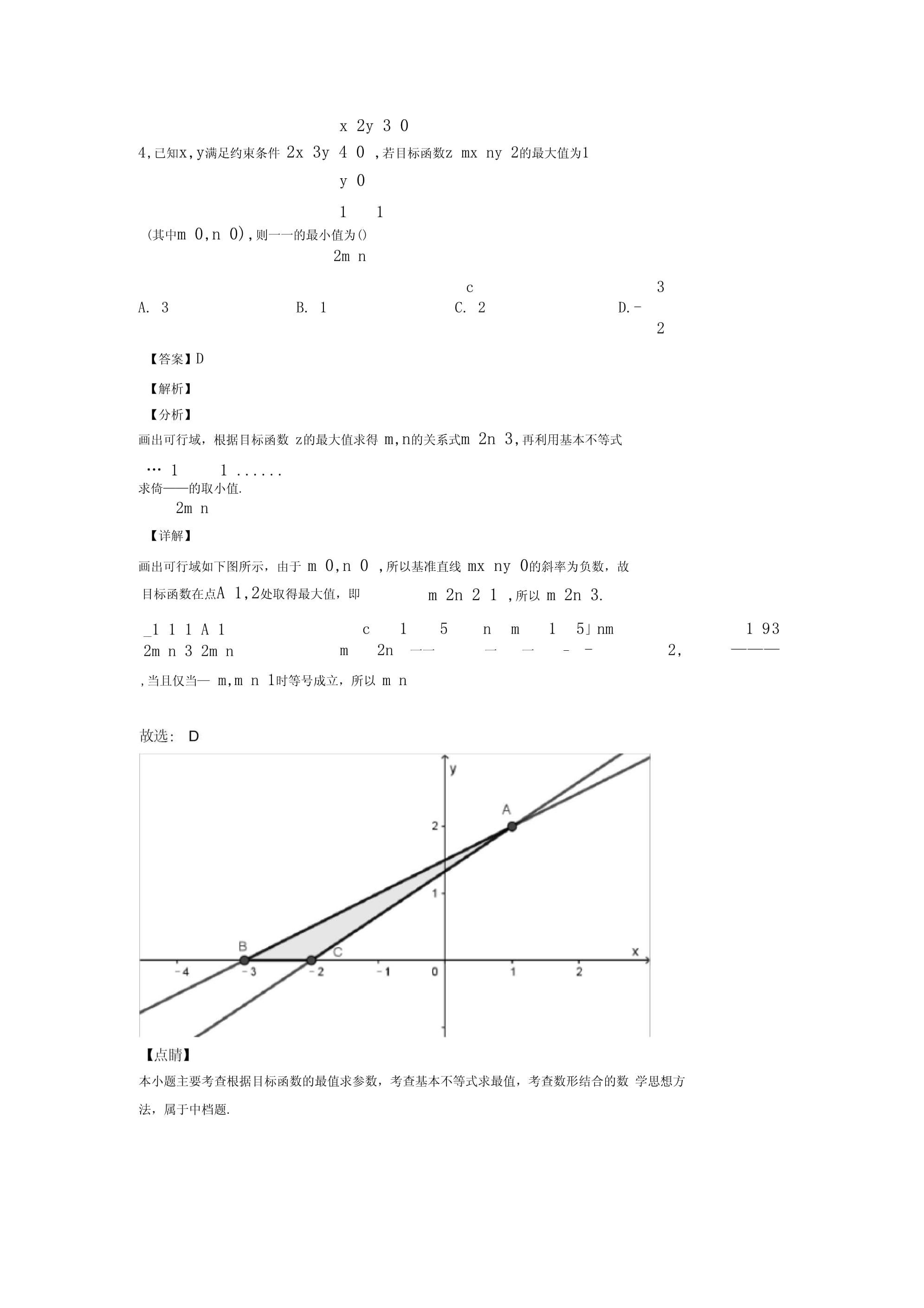
4、方程ax b x 30的解，从b0且一1 ,ax23 ,解集为 ，1 U 3,故选：A.【点睛】本题考查一元一次不等式、一元二次不等式的解集，考查学生的计算求解能力与推理能 力，属于基础题.x 2y 3 04,已知x,y满足约束条件 2x 3y 4 0 ,若目标函数z mx ny 2的最大值为1y 0 TOC o 1-5 h z 1(其中m 0,n 0),则一一的最小值为()2m nc3A. 3B. 1C. 2D.-2【答案】D【解析】【分析】画出可行域，根据目标函数 z的最大值求得 m,n的关系式m 2n 3,再利用基本不等式 11 求倚的取小值.2m n【详解】画出可行域如下图所示，由于

5、m 0,n 0 ,所以基准直线 mx ny 0的斜率为负数，故目标函数在点A 1,2处取得最大值，即m 2n 2 1 ,所以 m 2n 3._1 1 1 A 12m n 3 2m n,当且仅当 m,m n 1时等号成立，所以 m n本小题主要考查根据目标函数的最值求参数，考查基本不等式求最值，考查数形结合的数 学思想方法，属于中档题. TOC o 1-5 h z c15nm15nm1 93m2n一一一一-2,32mn32.mn32211 ,一，3的取小值为一.2m n25.已知点p, Q分别是抛物线x2 8y和圆x2 (y 2)2 1上的动点，点A(0,4),则| PA |2 一 .1PAL的

6、最小值为（） |PQ|1042.3 24.2 1PQ设出点P的坐标X0,y。，用y。表示出PA；根据圆上一点到定点距离的范围，求得的最大值，再利用均值不等式求得目标式的最值【详解】设点P xo,yo ,因为点p在抛物线上，所以2X。yo因为点 A(0,4)，则 |PA |2 X；y。4 2y。2y。 16.又知点Q在圆x2 （y 2）2 1上，圆心为抛物线的焦点F(0,2),妁|PQ|的值最小，则|PQ|的值应最大，即PQmaxPF1 V。 3.所以出|PQ|y 16y032y。 36 y。 325y03y。 325V。V。25V。当且仅当y02时等号成立.一| PA |2，一所以）L的最小值

7、为4.|PQ|故选：B.【点睛】本题考查抛物线上一点到定点距离的求解，以及圆上一点到定点距离的最值，利用均值不 等式求最值，属综合中档题.6.已知函数f x log2 JX21 x ,若对任意的正数 a,b ,满足3 1 f a f 3b 10,则一一的取小值为（）a bA. 6B. 8C. 12D. 24【答案】C【解析】【分析】先确定函数奇偶性与单调性，再根据奇偶性与单调性化简方程得a 3b 1 ,最后根据基本不等式求最值.【详解】因为J?1x Vx2 x x x 0,所以定义域为R,，1,因为f x log 2 f o ，所以f x为减函数 x2 1 x因为f x110g 2 | 2 ，

8、 f x,x 1 x10g2 Jx2 1 x，所以f x f x , f x为奇函数,因为f a f 3b 10,所以f a1 3b ,即 a 3ba 3b因为 9b a 219b a 6, a b a b一,3 1 一1.1所以一 一12 （当且仅当a b 时，等号成立），选 C.a b26本题考查函数奇偶性与单调性以及基本不等式求最值，考查基本分析求解能力，属中档题7 .已知 ，均为锐角，且满足sinsin2cos ,则的最大值为（）A.12B.C.一4D.一3利用两角差的正弦公式，将已知等式化简得到tan 3tan ,由，均为锐角，则的最大值，只需求出tan（）的最大值，利用两角差的正切

9、公式，将tan（ ）表示为tan的关系式，结合基本不等式，即可求解sin由2cos 整理得 sin2cos sinsin即 sin coscos sin2cossin ,化简得sincos 3cossin ,贝U tan3tan ,tan所以tantan2tan21 tantan1 3tan213tantan又因为为锐角，所以tan 0 ,2根据基本不等式13tan tan当且仅当tan3时等号成立,3因为,且函数y tanx在区间一，一 上单调递增,2 22 2则的最大值为-.6故选:B.【点睛】本题考查两角差最值，转化为求三角函数最值是解题的关键，注意应用三角恒等变换、基本不等式求最值，考

10、查计算求解能力，属于中档题8.已知不等式 x2 ax 4 0对于任意的x 1,3恒成立，则实数a的取值范围是（）A. （,5B. 5,）C （,4D. 4,）【答案】C【解析】4若不等式 x2 ax 4 0对于任意的x 1,3恒成立，则a x 对于任意的x 1,3恒x4成立，,当x 1,3时，x 4,5 , a 4,即实数a的取值范围是（，4,故选 xC .【方法点晴】本题主要考查利用导数求函数的最值以及不等式恒成立问题，属于难题.不等式恒成立问题常见方法：分离参数a f x恒成立（a f x max即可）或af xiiiax恒成立（a f x min即可）；数形Z合（y f x图象在y g

11、x上方即可）； 讨论最值f x min0或f x max 0恒成立； 讨论参数.本题是利用方法 求得a的取值范围的.x9 .若x, y满足约束条件 xx围是（）A. 1,）B.（【答案】A【解析】y 4 0,2 0, 且z ax y的最大值为2a 6 ,则a的取值范 y 2 0,1C. ( 1,)D. (,1)【分析】画出约束条件的可行域，利用目标函数的最值，判断a的范围即可.【详解】作出约束条件表示的可行域，如图所示.因为z ax y的最大值为2a 6 ,所以z ax y在点A(2,6)处取得最大值，则a 1,即a 1.故选：A【点睛】本题主要考查线性规划的应用，利用z的几何意义，通过数形结

12、合是解决本题的关键.10.抛物线F三二的焦点为F ,准线为l, A, B是抛物线上的两个动点，且满2 ，一 ，一，足AFB 设线段AB的中点3M在l上的投影为MN的最大值是()ABA J3A4【答案】B【解析】【分析】【详解】B.C.2试题分析：设A,B在直线l上的投影分别是A,B1，则是AB中点，所以MN二(AABBi )，则MNAF AA , BF 1 |aa| |bb|AFBFAB|AB2 ABABF中AB(AF(|af|ABAFBF )2BF )22BFAFAF BF cosBF (AFAFBFABAFBFAF BFBF )2AFBF)2 ；(AF4BF )2,所以2,3,所以3MNA

13、B考点：抛物线的性质.【名师点晴】在直线与抛物线的位置关系问题中，涉及到抛物线上的点到焦点的距离，焦点弦长，抛物线上的点到准线（或与准线平行的直线）的距离时，常常考虑用抛物线的定义进行问题的 转化.象本题弦 AB的中点M到准线的距离首先等于 A,B两点到准线距离之和的一半, 然后转化为A,B两点到焦点F的距离，从而与弦长 AB之间可通过余弦定理建立关系.11 .在三角形ABC中，给出命题P： ab c2”，命题q：C ，则p是4的（）3B.必要不充分条件A.充分不必要条件C.充分必要条件D.既不充分也不必要条件【答案】A【解析】【分析】由余弦定理将c2化为a2 b2 2abcosC ,整理后利

14、用基本不等式求得 1 2cosc 2, 求出C范围，即可判断充分性，取 a 4, b 7, c 6,则可判断必要性不成立，两者结合可得正确的选项.【详解】充分性：由余弦定理，c2 a2 b2 2abcosC ,所以 ab c2,即 ab a2 b2 2abcosC ,.2整理得，1 2cosC a, ab由基本不等式，a1ab当且仅当a b时等号成立,1_此时，1 2cosC 2,即 cosC 一,解得 C , 23充分性得证；必要性：取a 4, b 7, c6,则cosC16 49 36 29 12 4 756 2故C ,但ab 28 c2,故C 推不出ab c2.3故必要性不成立；故p是q

15、的充分不必要条件.故选：A【点睛】本题主要考查充分必要条件的判断、余弦定理的应用和基本不等式的应用，考查学生分析 转化能力，属于中档题.x y 2,.若变量x, y满足2x 3y 9,则x2+y2的最大值是x 0,A. 4B. 9C. 10D. 12【答案】C【解析】试题分析：画出可行域如图所示，点A (3,1)到原点距离最大，所以,22、一(x y )max 10 ,选 C.【考点】简单线性规划【名师点睛】本题主要考查简单线性规划的应用，是一道基础题目.从历年高考题目看，简单线性规划问题是不等式中的基本问题，往往围绕目标函数最值的确定，涉及直线的斜 率、两点间的距离等，考查考生的绘图、用图能

16、力，以及应用数学知识解决实际问题的能 力.1_. ,.已知函数f(x) - mcos2x (m 2)sin x,其中1 m 2,右函数f x的最大值 2记为g m ,则g m的最小值为()A.1B. 1C.s/3D. V3 1【答案】D【解析】【分析】, 、, 2,. m .f (x) msin x (m 2)sin x ，令 sin x t 1,1,则,2 ，m,my mt(m 2)t 一 ,结合 122 m2 (m 2)2y 1 1y tm 24m2m 2可得1jL m 1 ,再利用基本不等式即可得到答案m由已知，f （x）15 m(12、2sin x)2m(m 2)sin x msin

17、x (m 2)sin x 令 sinx t 1,1,则 ymt2(m 2)t m ,因为 1 m 2 ,2 2 m 111所以对称轴为t 2m1 0,1,所以2mm 22g m yt2m22) 3m 112JFI1屈1 当且仅当m 组时，等号成立.3故选：D【点睛】本题考查换元法求正弦型函数的最值问题，涉及到二次函数的最值、基本不等式的应用, 考查学生的数学运算能力，是一道中档题.14.若a、b均为实数，则 ab a b0”是 a b 0”的（）A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【答案】B【解析】【分析】通过列举，和推理证明可以推出充要性.【详解】若

18、ab a b 0 中，取 a= 1, b=2,则推不出a b0;若a b0 ,则a b0,则可得出ab a b 0 ； 故ab a b 0”是b0”的必要不充分条件，故选：B.【点睛】本题考查充分必要不条件的定义以及不等式的性质，可通过代入特殊值解决.15.若均不为1的实数a、b满足a b 0,且ab 1 ,则（）A. log a 3 logb3B. 3a 3b 6C. 3abi 3ab D. ab ba【答案】B【解析】【分析】举反例说明A,C,D不成立，根据基本不等式证明B成立.【详解】当 a 9,b 3时 loga3 10gb3；当 a 2,b 1 时 3abi3a b;当 a 4,b

19、2 时 abba;因为a b 0, ab 1 ,所以3a 3b综上选B.【点睛】2733r 2/3 2J32 . 6，本题考查比较大小，考查基本分析论证能力，属基本题16.已知直线y kx 2k 1与直线y值范围是（）1 一、xx 2的交点位于第一象限，则实数 k的取2A. k,1 -1B. k 或 k C.6 k 262D.y联立ykx 2k 11，可解得交点坐标（x,y）,由于直线y kx 2k 1与直线x 22一一 x 0y - x 2的交点位于第一象限，可得，解得即可.y 0【详解】y kx 2k 1解：联立 1,解得y x 22Q直线y kx 2k 1与直线y2 4kx 2k 1，6

20、k 1y 2k 11 八，、-x 2的交点位于第一象限,22 4k -02k 1 i 11,斛得： 一 k 一6k 1 0622k 1故选：D.【点睛】 本题考查两直线的交点和分式不等式的解法，以及点所在象限的特征.y x.若实数x, y满足不等式组 x y 1 ,则2x y的最小值是（）y 1A. 3C. 0D.3【答案】D【解析】【分析】根据已知的约束条件画出满足约束条件的可行域，再由目标函数z 2x y可得y 2x z,此时Z为直线在y轴上的截距，根据条件可求 Z的最小值.【详解】解：作出不等式组所表示的平面区域，如图所示得阴影部分的ABC,由z 2x y可得y 2x z ,则z为直线在

21、y轴上的截距y x 把直线l:y 2x向上平移到 A时，z最小，此时由 可彳# A( 1, 1)y 1-4二本题考查用图解法解决线性规划问题，分析题目的已知条件，找出目标函数中的z的意义是关键，属于中档题.一x 一 一2 一 一 .设集合 M x 0 , N x x 2x 0,则 M N为()x 1A. x 0 x 1 B. x 0 x 1C. x 0 x 2D, x 0 x 2【答案】B【解析】【分析】根据分式不等式和一元二次不等式的解法，求得集合M x0 x 1, N x|0 x 2,再结合集合交集的运算，即可求解.【详解】x2由题意，集合 Mx|- 0 x0 x 1, N x x 2x 0 x|0 x 2,所以 M N x0 x 1 .故选：B.【点睛】本题主要考查了集合的交集的概念及运算，其中解答中结合分式不等式和一元二次不等式的解法，准确求解集合 A,B是解答的关键，着重考查了计算能力.19.已知等差数列 an的公差d 0,且ai,a3,ai3成等比数列，若ai1, Sn为数列 42Sn 6的刖n项和，则的取小值为( )