《行列式的应用》ppt课件

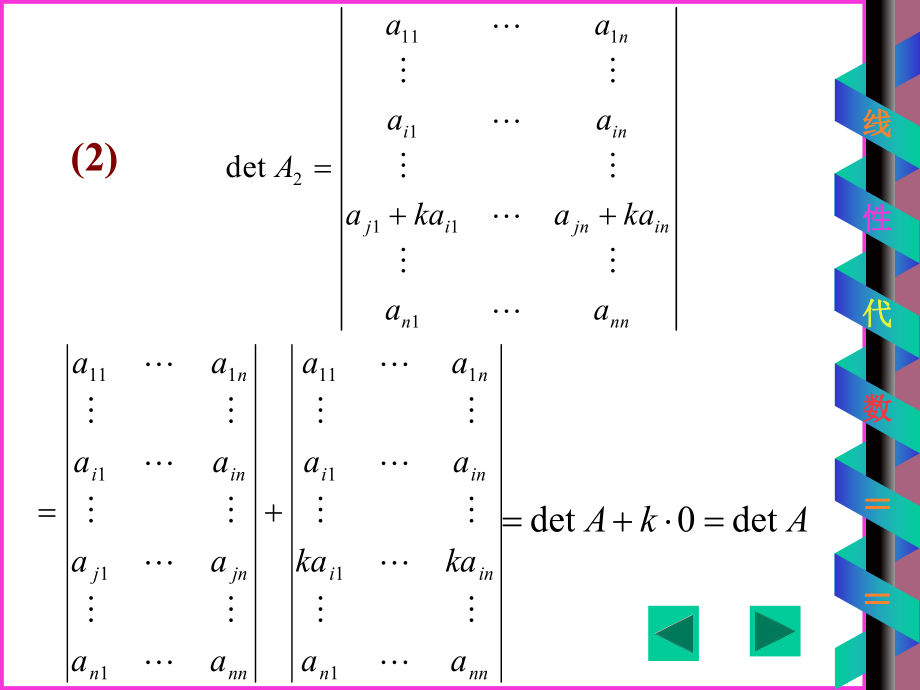
1、数数=线线性性代代2.2 2.2 行列式的运用行列式的运用行列式作为一中运算工具行列式作为一中运算工具,在很多方面都有广泛的运用在很多方面都有广泛的运用111211112121222212221212,nnnnnnnnnnnnAnaaaaaaaaaaaaAaaaaaa设 为一个 阶矩阵称行列式为方阵A的行列式,记为|A|或det(A).数数=线线性性代代证证(1)按乘以数按乘以数k的那一行展开，即得结的那一行展开，即得结论成立。论成立。假设把行初等变换施于n阶矩阵A上：(1) 将将A的某一行乘以数的某一行乘以数k得到得到A1，那么，那么 detA1 = k(detA)； (2) 将将A的某一行

2、的的某一行的k(0)倍加到另一行得到倍加到另一行得到A2 ,那么那么 detA2 = detA；(3) 交换交换A的两行得到的两行得到A3, 那么那么 detA3 = - detA.数数=线线性性代代11112111detniinjijninnnnaaaaAakaakaaannniniininnnnjnjininaakakaaaaaaaaaaaaa111111111111AkAdet0det(2)数数=线线性性代代例1 奇数阶反对称阵的行列式必为零.证 Ann (n为奇数)满足： Adet于于是是，T TAdet)det( A,detdet) 1(AAn0121030230例如,AAT T数数

3、=线线性性代代定义定义6 (伴随矩阵伴随矩阵)111211222212(),det( )( ,1,2, ).( )()12423431ijn nijijndefnnnnnAaAAai jnAAAAAAadj AAAAAAadj对于设 为中元素 的代数余子式则称 (2.8)为 的伴随矩阵 记为如1 1 伴随矩阵伴随矩阵数数=线线性性代代定理定理1*(2),|n nAnAAA AA I对于任何方阵以下成立证：证：11121111212122212222*1212|000|0|00|nnnnnnnnnnnnaaaAAAaaaAAAAAaaaAAAAAA IA数数=线线性性代代引理引理 1设L有如下分

4、块方式的(n+m)阶矩阵:( ),ijlA0 L=CB其中A是n阶矩阵,B是m阶矩阵,则有 |L|=|A|B|.引理引理 2设A、B皆为n阶矩阵，那么有(1) |,;(2) | |.nAARABA B 证明：略证明：略证明：略证明：略数数=线线性性代代定理定理2(方阵可逆的充要条件方阵可逆的充要条件)1*0,1n nAAAAAA方阵可逆且当 可逆时有证：证：,10ABABIA BA 设 可逆,则有使得*,0,11()()AAAA AA IAAA AIAA设则由 1*1AAA 110,aaa则注：数数=线线性性代代 例例 2 断定以下方阵能否可逆，假设可逆，求其逆矩断定以下方阵能否可逆，假设可逆

5、，求其逆矩阵阵333654321)2(;4321) 1 (BA解解1(1)2.214211*3131222AAAAA 故 可逆，且由求逆矩阵的公式，得不可逆故BB. 0)2(acbdbcaddcbabcab1, 01则有一般地，若数数=线线性性代代推论推论.,11IBAABBABAIABBAnnnn都可逆，且、则满足、若证：证：111111,1,0,0,ABIA BABABABIAA ABA IBAABBAA AI由、 都可逆.由两端左乘得即同理有且11111AAIA AAA 注: 数数=线线性性代代例例31*3 31,(3 )22ADAA设计算行列式解解11*11111311(3 ),3212332116().327AAAA AADAAAA 数数=线线性性代代例例4*1| (|)nAAA设 为n阶方阵,则 |证：证：*1*1*1*1(1)(2).0,()() 000,0,| 0.| 0| |nnnnAAA AA IA AA IAIAAAA AA IAAA AAAAAAAA* 若|A|0, 若|A|=0,则|A |=0.否则,若|A |0,即A 可逆由于 又当时这与相矛盾故综上所述,数数=线线性性代代 例例 5 .0 ,1 AIAIAA：证证明明且且设设T TAAAAI T T IAA T TT T)(