数学物理方法04

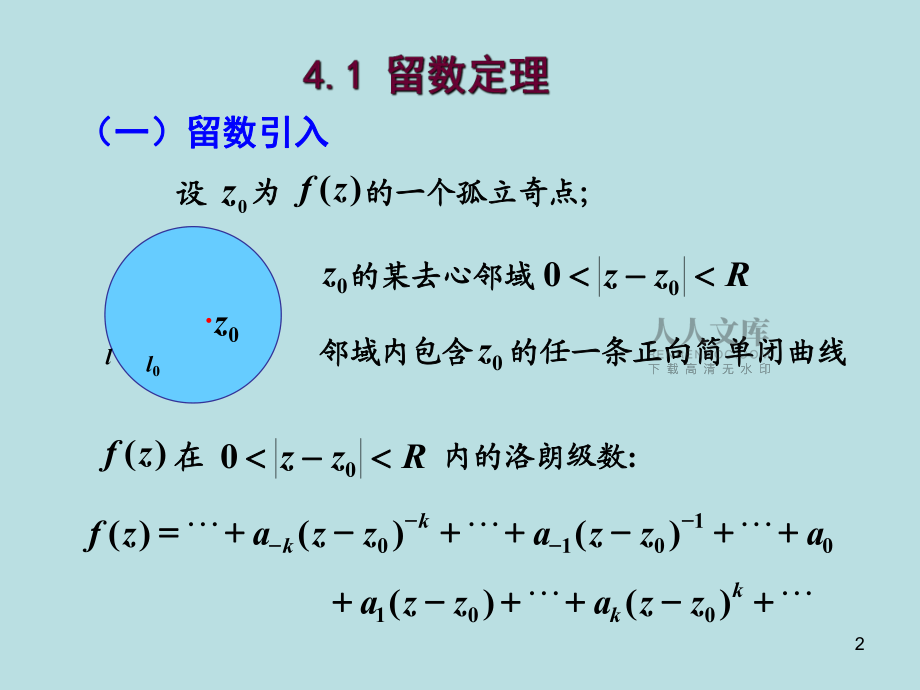
1、1目的与要求目的与要求：掌握留数的概念及计算方法。掌握掌握留数的概念及计算方法。掌握 用留数定理计算典型实定积分的方用留数定理计算典型实定积分的方 法。法。重点：重点：难点：难点：留数的计算与留数定理留数的计算与留数定理留数的计算与留数定理留数的计算与留数定理2（一）留数引入（一）留数引入0z)(zf设设为为的一个孤立奇点的一个孤立奇点; ;内的洛朗级数内的洛朗级数:)(zfRzz 00在在0z.的某去心邻域的某去心邻域0zRzz 00邻域内包含邻域内包含0z的任一条正向简单闭曲线的任一条正向简单闭曲线ll001010)()()(azzazzazfkk+ + + + + + + += = LL

2、LLL+ + + + + + +kkzzazza)()(001300 ( (柯西定理柯西定理)i 2LLL+ + + + + + += = l0l0kkzzzazzzad)(d)(1010LL+ + + + + + + + zzzazzzazakl0kl0l0d)(d )(d001012 = =ia的系数的系数洛朗级数中负幂项洛朗级数中负幂项101)( zza lzzfd)(积分积分0()Res f z=的留数的留数在在0)(zzfzzfiald )(211 = = 即即 = = + + rzznzzz0d)(1 10所所以以 = = = =. 0, 0, 0,2nni前面前面4（二）有限远留

3、数定理（二）有限远留数定理说明说明:2. 留数定理将沿留数定理将沿封闭曲线封闭曲线l积分转化为求积分转化为求被积函数在被积函数在l内各孤立奇点处的留数内各孤立奇点处的留数.1( )d2 iRes().njjlf zzf b =内部处处解析内部处处解析；上及上及在在llzf)(. 11.留数定理留数定理)(zf在区域在区域 B内除有限个孤内除有限个孤12,nb bbL外处处解析外处处解析, l 是闭区域是闭区域B包围诸奇包围诸奇点的一条正向简单闭曲线点的一条正向简单闭曲线, , 那么那么立奇点立奇点函数函数5证证12( )d( )d( )dlllnf zzf zzf zz+L( )dlf zz

4、=12111( )d( )d( )d2 i2 i2 illlnf z zf zzf z z +L12( )( )( )ResResResnf bf bf b=+L两边同时除以两边同时除以 且且2 i 1b2bnbBLl.由复连通域的柯西定理由复连通域的柯西定理.),(Res1即可得即可得 = = =njbjf62.2.留数的计算方法留数的计算方法(1) 如果如果0z为为)(zf的可去奇点的可去奇点, , 0(). 0Res f z=则则0000()lim()(. )Reszzf zzzf zz=如果如果 为为 的一阶极点的一阶极点, , 那末那末0z)(zf规则规则1 1(2) 如果如果0z为

5、为的本性奇点的本性奇点, , )(zf(3) 如果如果0z为为的极点的极点, , 则有如下计算规则则有如下计算规则)(zf)(zf展开展开则需将则需将成洛朗级数求成洛朗级数求1 a7例例1 求求nzzezf= =)(在在0= =z的留数的留数.解解阶极点，阶极点，的的是是因为因为nzfz)(0= = Res0f所所以以.)!1(1 = =n = = nznnnzzezzn110ddlim)!1(1如果如果 为为 的的 阶极点阶极点, 0z)(zfm100101()lim()( )(1)!.dResdmmmzzf zzzf zmz=规则规则2 2那末那末8例例2 求求51)(zezfz = =在

6、在0= =z的留数的留数. .解解 0= =z是是)(zf的四阶极点的四阶极点. + + + + + + + += = 1! 6! 5! 4! 3! 21116543255Lzzzzzzzzez,! 6! 51! 41! 31! 211234L+ + + + + + += =zzzzz1(0)Res fa=所所以以.241! 41= = =在在+ + z0内将内将展成洛朗级数展成洛朗级数:)(zf9例例3 计算积分计算积分2,(1)zlezz z dl为正向圆周为正向圆周:. 2= =z解解20(0)lim(1)=Reszzefzz z20lim1(1)zzez=2211(1)lim(1)(2

7、 1)!(1)dResdzzefzzz z=0= =z为一级极点为一级极点,1= =z为二级极点为二级极点, = =zezzzddlim121)1(limzzezz = =, 0= =2(1)zlezz z d所所以以210i() =+2(0)(1)i ResResff =+2 i. =10规则规则3 3 如果如果,0)(,0)(,0)(000 = = zQzQzP设设,)()()(zQzPzf= =)(zP及及)(zQ在在0z都解析都解析，那末那末0z为为的一阶极点的一阶极点,)(zf000(.)()ResP zf zQ z= 且有且有例例4 求求6sin)()()(zzzzQzPzf =

8、= =在在0= =z的留数的留数.分析分析,0)0()0()0(= = = = = =PPP.0)0( P0= =z是是zzsin 的三阶零点的三阶零点由规则由规则2得得的三阶极点的三阶极点，是是所以所以)(0zfz = =1123260103 1dsinRes( )lim.()!dzzzfzzz=计算较麻烦计算较麻烦. .如果利用洛朗展开式求如果利用洛朗展开式求1a较方便较方便: + + = = L! 5! 31sin5366zzzzzzzz 115Res0.!fa= ,!5!353L+ + = =zz解解12（三）无穷远点的留数（三）无穷远点的留数即即 1( )2 ilf zz = d记作

9、记作1( )( )2Resdilff zz =1.1.定义定义设函数设函数)(zf在圆环域在圆环域+ + zR内解析内解析，l为圆环域内绕原点的任何一条正向简单闭曲线为圆环域内绕原点的任何一条正向简单闭曲线，1)(Res = =af1 = =a1( )2dilf zzl 那那末末积分分的的值与与 无无关关， ，则称此定值则称此定值点的留数点的留数，在在为为 )(zf13.1z.2z.kz .证证1( )()ResResnkkff z= +111( )( )22llf zzf zz =+ddii. 0= =由留数定义有由留数定义有:(绕原点的并将绕原点的并将kz内部的正向简单闭曲线内部的正向简单

10、闭曲线)l包含在包含在 2. 2.留数和定理留数和定理如果函数如果函数)(zf在扩充复平面内只有有限个在扩充复平面内只有有限个孤立奇点孤立奇点, ,那末那末在所有各奇点在所有各奇点( (包括包括 点点) ) 的留数的总和必等于零的留数的总和必等于零.)(zf14说明说明: 由定理得由定理得1()(),ResResnjjf zf= 1( )2()diResnjjlf zzf z =( (留数定理留数定理) )2().iRes f = 计算积分计算积分计算无穷远点的留数计算无穷远点的留数.( )lf zzd优点优点: : 使计算积分进一步得到使计算积分进一步得到简化简化. . ( (避免了计算诸有

11、限点处的留数避免了计算诸有限点处的留数) )15说明说明: 0z如如 为为 m 阶极点，当阶极点，当 m 较大而导数又难以计算时较大而导数又难以计算时, 可直接展开洛朗级数求可直接展开洛朗级数求1a来计算留数来计算留数 .56560106 1dsinRes( )lim()!dzzzfzzz=.! 51 = =2. 在应用规则在应用规则2 2时时, 取得比实际的阶数高取得比实际的阶数高. .阶数高反而使计算方便阶数高反而使计算方便. . :6= =m 1. 在实际计算中应灵活运用计算规则在实际计算中应灵活运用计算规则. 为了计算方便一般不要将为了计算方便一般不要将m但有时把但有时把m取得比实际的

12、取得比实际的如上例取如上例取16 解：共有七个奇点：解：共有七个奇点：前前6 6个根均在内部，故由留数和定理可用求个根均在内部，故由留数和定理可用求无限远奇点留数解此题。即无限远奇点留数解此题。即iz = 420 1 2 3, , ,kzk=z4=z 2 iRezIs f z = 例5 计算 152342412dzzIzzz=+ 而而 故故 。从而。从而 1523241624112121 31211zf zzzzzzz= + + + LL 11Rezs f za= = 2 iI =17 4.1 1.（1）（3）（5）（7）（9） 2. （1）（3） 3.1819 设法把实变函数定积分跟复变函数

13、回路积分联系设法把实变函数定积分跟复变函数回路积分联系起来。起来。 留数定理是复变函数的定理，若要在实变函数留数定理是复变函数的定理，若要在实变函数定积分中应用，必须将实变函数变为复变函数。这定积分中应用，必须将实变函数变为复变函数。这就要利用解析延拓的概念。就要利用解析延拓的概念。留数定理计算实变函数定积分原理留数定理计算实变函数定积分原理：200ab()bafx dx 如图，对于实积分如图，对于实积分 ，变量变量 x 定义在闭区间定义在闭区间 a,b (线段线段l1 )，此区间应是回路此区间应是回路l=l1+l2的一部分。实的一部分。实积分要变为回路积分，则实函数必须积分要变为回路积分，则

14、实函数必须解析延拓解析延拓到复到复平面上包含回路的一个区域中，而实积分成为回路平面上包含回路的一个区域中，而实积分成为回路积分的一部分：积分的一部分：1l2l2( )()( )bllaf z dzf x dxf z dz= =+ + 左边可以利用留数定理，右边对左边可以利用留数定理，右边对l2 的积分在解析的积分在解析延拓允许的情况下，可以自由选择，通常选择延拓允许的情况下，可以自由选择，通常选择l2 使积使积分最易完成。分最易完成。21 20d)sin,(cos R思想方法思想方法 :封闭路线的积分封闭路线的积分 . .两个重要工作两个重要工作: : 1) 1) 积分区域的转化积分区域的转化

15、2) 2) 被积函数的转化被积函数的转化把定积分化为一个复变函数沿某条把定积分化为一个复变函数沿某条 iez = =令令 ddiiez = =,ddizz= = )(21sin iieei = =,212izz = =)(21cos iiee + += =,212zz + += =当当 历经变程历经变程2,0时时,1= =z的的正方向绕行一周正方向绕行一周. .z 沿单位圆周沿单位圆周22 d )sin,(cos20 RizzizzzzRzd21,21122 = = + += =zzfzd )(1 = = =z的有理函数的有理函数 , , 且在且在单位圆周上分母不单位圆周上分母不为零为零 ,

16、, 满足留数定满足留数定理的条件。理的条件。包围在单位圆周包围在单位圆周内的内的诸孤立奇点诸孤立奇点。12iRes().nkkf z=23例例1 计算积分计算积分)0(dcossin202 + + baba 解解, iez = =令令则则,21sin2ziz = = ,21cos2zz + += = ,dd iiez = =izzzzbazzbazd2114)1(dcossin21222202 + + + = =+ + = = = =+ + + = =12222d)2(2)1(zzbazbzizz24222222bbaba = =).(2222baab = = = = + + = =12222

17、2222d)1(zbbaazbbaazbizzz22()2(0)()ResResaabiffb +=+25例例2 解解 , 10 p由由于于)cos1(2)1(cos2122 + + = =+ + pppp内内不不为为零零，在在20 故积分有意义故积分有意义.)(212cos22 iiee + += =由由于于),(2122 + += =zzizzpzzpzzIzd2211221122 + + + + += = = = .)10(dcos21cos2202的值的值计算计算 + + = = pppI 26izzpzzpzzIzd2211221122 + + + + += = = = zpzpzi

18、zzzd)(1(21124 = = + += =,1, 0ppz = =被积函数的三个极点被积函数的三个极点内内，在在圆圆周周1, 0= = =zpz0zzp=且为二阶极点，为一阶极点，.d )(1zzfz = = =上被积函数无奇点，上被积函数无奇点，所以在圆周所以在圆周1= =z2742201(0)lim2(1)()dResdizzfzzzpz zp+=223422220()4(1)(12)lim2 ()izzpzpp zzzpzpzpzpp z+=+221,2ipp+= 4221,2(1)ippp+=421( )lim ()2(1)()Resizpzf pzpzpz zp+=222221

19、1222(1)iiippIppp+=+.1222pp = =因此因此28例例3证证 时时当当xz = =222cossin=+ixexix如图路径如图路径，oxyRRADB20,idzl OA AB BAez=+=0222240200,iiiii4ididdiR er exRReR eeerex +=2220,iiidddxzzOAABBOezezez+=.221dcosdsin0202= = = xxxx证明证明2ize设函数设函数29时，时，当当 R24042iidreere=1.2222i=+22222240400iicossiniiddidRxRRrRexeReeer =42sin y

20、=sin2/4y=4/注意：由图可得出注意：由图可得出30220 xxx+(cosisin)d.221= =1222=+i.2令两端实部与虚部分别相等，得令两端实部与虚部分别相等，得 02dcosxx = =02dsinxx菲涅耳菲涅耳(fresnel)(fresnel)积分积分 404d2 ReR).1(42ReR = =0 R222cos2sin2sin24400iiiddRRReR eeR 31( )( )0f zzzf z 复复变变函函数数在在实实轴轴上上无无奇奇点点，在在上上半半平平面面除除有有限限个个奇奇点点外外是是解解析析的的；且且当当在在上上半半平平面面和和在在实实轴轴上上时时

21、，一一致致地地。11112( )( ),( )( )( )(,)nnnmmmxa xaxf xxxb xbxxxmn +=+LL该该条条件件意意味味着着：即即没没有有实实的的零零点点，的的次次数数至至少少高高于于两两次次。()()( )ddxxf xxx +=分析分析可先讨论可先讨论( )d ,RRf xx最后令最后令R 即可即可 . .32lim( )( )( )lim( )RRRRRRIf x dxRf x dxf x dxf x dx= =即即把把积积分分表表为为：若若时时，上上述述极极限限存存在在，则则该该极极限限称称为为的的主主值值，记记作作：下面分析中采用下面分析中采用“围道积分法

22、围道积分法”和和留数定理计算！留数定理计算！ 首先把积分转化为围道积分，即首先把积分转化为围道积分，即d( )RRxf x( )dlf zz33xy0R .R.这里可补线这里可补线RC( (以原点为中心以原点为中心 , R为半径为半径的在上半平面的半圆周的在上半平面的半圆周) )RC与与 RR, 一起构成封闭曲线一起构成封闭曲线l , f(z)在在l及其及其内部内部( (除去有限孤立奇点）处处解析除去有限孤立奇点）处处解析.取取R适当大适当大, , 使使f(z)所有的在上半平面内的极点所有的在上半平面内的极点kz都包在这积分路线内都包在这积分路线内. .RC34根据留数定理得根据留数定理得 :

23、 :( )( )2(),ddiResRkRCRf xxf zzf z+=111111( )1nnm nmma za zf zb zb zz+=+LL1111111nnm nmma za zbzb zz+LL当当 充分大时充分大时, , 总可使总可使z111,nna za z+L111,2mmb zb z+L35，因因为为2 nm111111( )1nnm nmma za zf zbzb zz+LL所所以以24z( )( )ddCCRRf zzf zz24RR4,R=( )2()=diReskf xxf z所所以以:( )0;dCRRf zz+( ),df xx( )dRRf xx36例例4 计

24、算积分计算积分), 0, 0()()(d22222bababxaxx + + + + + 222221( )() ()f zzazb=+2221() ()iiz azazb=+解解 在上半平面有二在上半平面有二 阶极点阶极点, iza=. izb=一阶极点一阶极点2221,2()i b ab=()Resif a372221() ()iiz bzazb=+2232223,4()ibaaba= 2 Re( )isiResif bf a=+.)(2 )2(23bababa+ + += =2232222223124()2 ()iiibaabab ba =+Re()sif b + + + + +)()(

25、d22222bxaxx所以所以38xy0R .R.( )( )( )(0)iiddxa xa xxF x exexa +=积分存在要求积分存在要求: F(x)是是x的有理函数而分母的次的有理函数而分母的次数至少比分子的次数高一次数至少比分子的次数高一次, , 并且并且F(z)在实轴上在实轴上RC与与 RR, 曲线曲线l ,使使F(z)所有的在上半平面内的极点所有的在上半平面内的极点kz包在这积分路线内包在这积分路线内 . .同前一型同前一型: : 补线补线RC一起构成封闭一起构成封闭都都RC无孤立奇点无孤立奇点.（或（或F(x)当当z在上半平面及实轴上在上半平面及实轴上 时一致的时一致的 :约

26、当引理）约当引理）039( )( )iidda za zCCRRF z ezF z ez()2iidaxyCResR+对于充分大的对于充分大的 , 且且 时时, , 有有z1 nm2( )F zz sin,cosRyRx= = =令令zsdd = =id(Re) =.d R= =(cosisin)zR =+0 2i(i )daxyCResR+2idaxayCReesR= d20sin = =aRe40).1 (2aReaR = =,d420)2( aResin02daRe= d420sin = =aRe oy2 = =y sin= =y2 + + R0从而从而210i( )d().a zaRC

27、RF z ezeaR0i( )d.a zCRF z ez 41ii( )d( )dRa xa zRCRF x exF z ez+2iRes()a zkkiF z e=由留数定理由留数定理: :+ + R2ii( )diRes()a za xkkF x exF z e+=icosisinaxeaxax=+( )cosdi( )sindF xax xF xax x+2iiRes().a zkkF z e=42例例5 计算积分计算积分 .0, 0,d)(sin0222 + + + +amxaxmxx解解 + + + + += =+ +xaxmxxxaxmxxd)(sin21d)(sin2220222

28、2 212iImd()mxxexxa+=+在上半平面只有二级极点在上半平面只有二级极点222=+i( ),()mzzf zezai,za=又又43xeaxximxd)(222 + + + +则则2iidRes( i)d()mzz azf aezzai=+,4maeam = =122ImiRes( i)f a =.4maeam = =2 iResif a =xaxmxxd)(sin0222 + + +所以所以注意注意 以上两型积分中被积函数中的以上两型积分中被积函数中的R(x)在实轴在实轴上无孤立奇点上无孤立奇点.44 F(x) 为z的有理函数的有理函数 , 且在单位圆周上分母不为零且在单位圆周

29、上分母不为零 , 满足留数定满足留数定理的条件。理的条件。 zk为为包围在单位圆周内的包围在单位圆周内的诸孤立奇点诸孤立奇点。 d )sin,(cos20 Rzzfzd )(1 = = =12iRes().nkkf z=类型一：类型一：()()()+=ddxfxxxx 类型二：类型二：( )( )0( )( )f zzzf zxx 复复变变函函数数在在实实轴轴上上无无奇奇点点，在在上上半半平平面面除除有有限限个个奇奇点点外外是是解解析析的的；且且当当在在上上半半平平面面和和在在实实轴轴上上时时，一一致致地地。这这实实际际上上意意味味着着的的次次数数至至少少高高于于两两次次。( )( )( )(

30、0)iiddxa xa xxF x exexa +=类型三：类型三：F(x)是是x的有理函数而分母的次数至少比分子的次数高一次的有理函数而分母的次数至少比分子的次数高一次, 并且并且F(z)在实轴上在实轴上无孤立奇点无孤立奇点.（或（或F(x)当当z在上半平面及实轴上在上半平面及实轴上 时一致的时一致的 :约当引理）约当引理）045CRa-RRCa+a-( )d( )d( )d( )d(dz=)RaRlRaCCf zaazf xxf xxf zzf zz +=+为为圆圆数数 为为径径圆圆绕绕过过点点 ，图图。以以心心，以以充充分分小小的的正正半半作作弧弧奇奇构构成成如如所所示示回回路路0004

31、,Re( );( )d( )d( )dlim( )d,lim( )diRe( )RaaCRCRisf zf x xf x xf x xf z zf z zs f a +=上上半半平平面面取取极极限限则则：左左边边2 2：待待求求积积分分右右边边第第3 3项项：（由由约约当当引引理理) )右右边边第第 项项：右边1、2项dii( )Re( )Re( )f xxsf zs f a =+上上半半平平面面2 2（四）实轴上有单极点的情况（四）实轴上有单极点的情况( )d ,( )( )2f xx f xzf x =在在实实轴轴上上有有某某个个单单极极点点；满满足足类类型型 的的条条件件4601= =+

32、=lim( )diRe( )( )( )(),()Cf zzsf af zzaaf zP zazaza 项项：将将邻邻开开为为级级数数单单点点，第4在在的的域域展展洛洛朗朗是是极极CRa-RRCa+a-000000=()()dmax()|d |max(),()()lim()lim()dCCCCP zaCP zazP zazP zaza P zaaP za dzP zaz 级级数数连连续续。表表示示的的解解析析部部分分，在在上上且且有有界界有有界界即即00111110= = =+iidd()ididilim( )diRe( )( )diRe( )iRe(z)CCCaaazzaeaazazaef

33、zzsf af xxsf zsf 上上半半平平面面实实轴轴2 2而而47=+( )( )dRe( )Re( )f zf x xisf zisf a 上上半半平平面面实实轴轴个个单单 点点, ,满满 类类条条2 2若上有1极足 型2 件=+( )Re( )Re( )f x dxisf zisf z 上上半半平平面面实实轴轴实实轴轴个个单单点点则则2 2若上有有限极.C 闭闭线线实实轴轴点点单单点点阶阶点点点点注意：1不是合曲2.上的奇只能是极，不能是2或以上的极，更不能是本性奇48.dsin21dsin0 xxxxxx + + + += =例例5 计算计算狄利克雷积分狄利克雷积分.dsin0 x

34、xx + +分析分析 所所以以是是偶偶函函数数 ,sinxxzzsin 某封闭曲线某封闭曲线+ ,因因zzsin在实轴上有一级极点在实轴上有一级极点, 0= =z应使封闭路应使封闭路线不经过奇点线不经过奇点, , 所以可取图示路线所以可取图示路线: :49xyoRCrCrRr R 解解 0iiiidddd,zxzxrRCRCrRreeeezxzxzxzx+=封闭曲线封闭曲线l: RrCrRCrR,+ + + + +由柯西定理得由柯西定理得:iiddxtrrRReextxt=id ,xRrexx= ，令令tx = =2iisin,ixxeex=由由5020iisiniddd,zzRrCCRrxe

35、exzzxzz+=知知iiddzzCCRReezszzseRRCyd1 = = = =0sin deR d220sin = =Re d220)2( Re),1(ReR = =+ + R于于是是0idzCRezz充分小时，充分小时，当当r512123ii( )i!nnzzzg zn= +LL当当 充分小时充分小时, 总有总有 z, 2)( zg0iididCrzrezre =, = = i1idd( )d ,rrrzCCCezzg zzzz=+112iii!znnezzzzn=+ +LL),(1zgz+ += =ld52,2d2 = = rCrs 0r即即0idizCrezz=+20iisini

36、ddd,zzRrCCRrxeexzzxzz+=02sinidi,xxx+=, 0d)( rCzzgi,=szgzzgrrCCd)(d)( 因为因为.2dsin0 + += =xxx所以所以535455221412bazlaedzaIea=222222/2/2000/2( ) 0( ) 0 babaaR iyaRaya R iybaRaxaxRed iyeedyRed iyRedx Redxa + = 56 4.2 1.(1)(2)(6) 2. (1)(2)(6) 3.(2)(4)(6)57如果如果 为为 的的 级极点级极点, 0z)(zfm100101()lim()( )(1)!.dResdm

37、mmzzf zzzf zmz=附录附录1 1：规则规则2 2证证那末那末+ + + + + = = 2020)()()(zzazzazfmmLL+ + + + + + + )()(010101zzaazza101010)()()()( + + + + + + += = mmmmzzazzaazfzzLL+ + + + + + +10100)()(mmzzazza(3) 如果如果0z为为的极点的极点, , 则有则有)(zf58+(含有含有 正幂的项正幂的项)0zz ).()(ddlim)!1(10110zfzzzmmmmzz = = )()(dd011zfzzzmmm 两边求两边求1 m阶导数阶导数, 得得1)!1( = =am,)!1()()(ddlim10110 = = amzfzzzmmmzz1)(Res = = az0f所以所以59规则规则3 3 如果如