新北师大版九年级下册1.6 利用三角函数测高(第1课时)演示文稿1

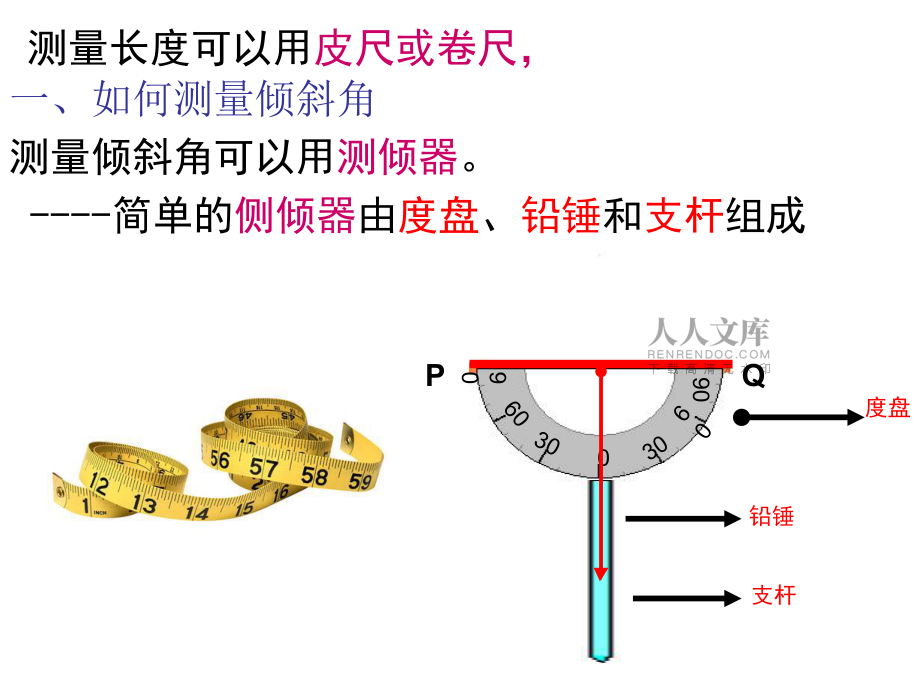
1、第一章 直角三角形的边角关系1.6 利用三角函数测高(第1课时)测量倾斜角可以用测倾器。 -简单的侧倾器由度盘、铅锤和支杆组成0303060609090PQ度盘铅锤支杆测量长度可以用皮尺或卷尺，一、如何测量倾斜角1 1、把支架竖直插入地面，使支架的中心线、把支架竖直插入地面，使支架的中心线、铅锤线和度盘的铅锤线和度盘的0 0刻度线重合，这时度盘刻度线重合，这时度盘的顶线的顶线PQPQ在水平位置。在水平位置。0303060609090M2 2、转动度盘，使度盘的直径对准目标、转动度盘，使度盘的直径对准目标M M，记，记下此时铅垂线所指的读数。下此时铅垂线所指的读数。M0303060609090

2、所谓所谓“底部可以到达底部可以到达”就是在地面上可以无障就是在地面上可以无障碍地直接测得测点与被测物体的底部之间的距离碍地直接测得测点与被测物体的底部之间的距离. . 如图，要测量物体如图，要测量物体MNMN的高度，可按下列步骤进行：的高度，可按下列步骤进行：1、在测点A安置测倾器，测得M的仰角MCE=；2、量出测点A到物体底部N的水平距离AN=l；3、量出测倾器的高度AC=a，可求出MN的高度。ANCME17.3生活应用如图，测倾器距某中学主楼的距离是30m，此时测得主楼顶部的仰角是30，测倾器的高度1.4m，求学校主楼的高度。（精确到0.1米） A M 30D解:过A作AMCD，在RtAD

3、M中，则AB=CM=1.4, tanDMDAMAMtanDMAMDAM，3303DM 即所以，CD=17.32+1.4=18.7米 答：学校主楼的高度是18.7米。 所谓所谓“底部不可以到达底部不可以到达”就是在地面上不可以直接就是在地面上不可以直接测得测点与被测物体之间的距离。测得测点与被测物体之间的距离。 如图，要测量物体如图，要测量物体MNMN的高度，可按下列步骤进行：的高度，可按下列步骤进行：,tantanMEMEb MNMEaACBDMNE1、在测点A处安置测倾器，测得此时M的仰角MCE=；2、在测点A与物体之间B处安置测倾器，测得此时M的仰角MDE=；3、量出测倾器的高度AC=BD

4、=a，以及测点A,B之间的距离AB=b.根据测量数据,可求出物体MN的高度。课题在平面上测量地王大厦的高AB测量示意图测得数据测量项目CD的长第一次30 1644 3560.11m第二次29 4445 2559.89m平均值下表是小亮所填实习报告的部分内容下表是小亮所填实习报告的部分内容: :C CE ED DF FA AG GB B生活应用3060m45452. 在在RtAEG中，中，EG=AG/tan30=1.732AG 在在RtAFG中，中， FG=AG/tan45=AG EG-FG=CD 1.732AG-AG=60 AG=600.73281.96 AB=AG+183(m)答案：答案：C

5、 CE ED DF FA AG GB B 1.(20051.(2005深圳深圳) )大楼大楼ADAD的高为的高为100100米米, ,远处有一塔远处有一塔BC,BC,某人在楼底某人在楼底A A处测得塔顶处测得塔顶B B处的仰角为处的仰角为6060, ,爬到楼顶爬到楼顶D D测得塔顶测得塔顶B B点仰角为点仰角为3030, ,求塔求塔BCBC的的高度高度. .课内拓展应用EF100603060 2.如图,在离铁塔150米的A处,用测角仪测得塔顶的仰角为30,已知测角仪高AD=1.5米,求铁塔高BE. (1)侧倾器的使用 (2)误差的解决办法-用平均值总结 测量底部可以到达的物体测量底部可以到达的物体的高度，如左图的高度，如左图测量底部不可以直接测量底部不可以直接到达的物体的高度，到达的物体的高度，如右图如右图ACMENACMENDB1. 分组制作简单的测倾器.2.选择一个底部可以到达的物体,测量它的高度并撰写一份活动报告,阐明活